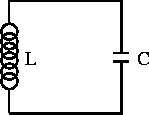
Figure 2.3: LC circuit.
Lets now consider the LC circuit in figure 2.3 which has no resistive element.
Kirchoff's voltage law applied to the loop is
![]()
Substituting our previous expressions for ![]() and
and ![]() gives
gives
![]()
Using I = dQ/dt gives
![]()
The circuit equation is second-order in Q and one possible solution is
![]()
where ![]() is the initial charge on the capacitor and
is the initial charge on the capacitor and ![]() is an arbitrary phase constant.
Considering the cases of
is an arbitrary phase constant.
Considering the cases of ![]() , gives
, gives ![]() .
The angular frequency
.
The angular frequency ![]() is totally determined by the other
parameters of the circuit
is totally determined by the other
parameters of the circuit
![]()
and ![]() is the natural or resonance frequency of the circuit.
is the natural or resonance frequency of the circuit.
We can also solve for the current and voltage across the capacitor
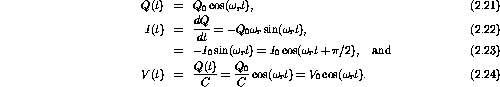
Notice that unlike the transient current and voltage responses of the RC and RL circuits, the LC circuit oscillates. The energy in the circuit is shared back and forth between the inductor and capacitor.