Integrating a two-form over a region in \mathbb{R}^2

Section 5.3 Integrating a two-form over a region in $R^{2}$

Step 2: we define the integral of a two-form on

U \subset R^{2}

along a closed bounded domain in

U

with a choice of orientation. The definition is in terms of standard double integrals from calculus. We show that the resulting integral is invariant under orientation-preserving reparametrizations, and changes sign under orientation-reversing reparametrizations. This is closely connected to the transformation formula for double integrals.

🔗

Objectives

You should be able to:

Define the integral of a two-form over a closed bounded region in $R^{2} .$
Show that invariance under orientation-preserving reparametrizations recovers the transformation formula for double integrals.

🔗

Subsection 5.3.1 The integral of a two-form over an oriented closed bounded region in $R^{2}$

🔗

We define the integral of a two-form over an oriented closed bounded region in

R^{2} .

🔗

Definition 5.3.1. Integral of a two-form over an oriented closed bounded region in $R^{2}$ .

Let $D \subset R^{2}$ be a closed bounded region. Let $(x, y)$ be coordinates on $R^{2} .$ The canonical ( $+$ ) orientation on $D$ is described by the ordered basis ${e_{1}, e_{2}}$ for $R^{2},$ with $e_{1} = (1, 0)$ and $e_{2} = (0, 1)$ the unit vectors pointing in the positive $x$ - and $y$ -directions. Let $ω = f d x \land d y$ be a two-form on an open subset $U \subseteq R^{2}$ such that $D \subset U .$ Then, we define the integral of $ω$ over $D$ with canonical orientation as:

\int_{D_{+}} ω = \iint_{D} f d A,

where on the right-hand-side we mean the standard double integral from calculus of the function $f$ over the region $D .$ If $D$ is given the opposite orientation, we define the integral of $ω$ over $D_{-}$ as:

\int_{D_{-}} ω = - \iint_{D} f d A .

🔗

Remark 5.3.2.

A bit of notation: we will always use double or triple integral signs to denote the standard double and triple integrals from calculus, while we will use only one integral sign when we are integrating a differential form.

🔗

It is probably worth recalling here how double integrals are defined, from your previous calculus course. If

D

is a rectangular domain, that is,

D = {(x, y) \in R^{2} | x \in [a, b], y \in [c, d]},

🔗

then the double integral is defined as an iterated integral:

\iint_{D} f d A = \int_{c}^{d} \int_{a}^{b} f d x d y .

🔗

The notation here means that the inner integral is an integral with respect to

x

(while keeping

y

fixed), while the outer integral is with respect to

y .

¹ We recall Fubini's theorem, which states that the order of integration does not matter:

\int_{c}^{d} \int_{a}^{b} f d x d y = \int_{a}^{b} \int_{c}^{d} f d y d x,

🔗

that is, it does not matter whether you integrate in

x

first and then in

y

or the other way around.

Note that on the right-hand-side here there is no wedge product: this is not the integral of a two-form, it is an interated integral in

x

and

y

as you have seen in calculus. The inner integral is with respect to

x

(keeping

y

fixed), while the outer integral is with respect to

y .

🔗

To integrate over a more general closed bounded region

D,

we proceed as follows. Since

D

is bounded, we can take it to be inside a rectangular region. We can then extend the function

f

to the rectangular region by setting it to zero everywhere outside

D .

The double integral over

D

is then defined to be the integral of the extended function over the rectangular region, which can be written as an iterated itegral as above.

🔗

There are two types of regions that give rise to nice iterated integrals. If

D

can be written as follows:

D = {(x, y) \in R^{2} | x \in [a, b], u (x) \leq y \leq v (x)},

🔗

with

u, v : R \to R

continuous functions, we say that the region is

x

-supported (or of type I ). In this case, one can show that the double integral can be written as the following iterated integral:

\iint_{D} f d A = \int_{a}^{b} \int_{u (x)}^{v (x)} f d y d x,

🔗

where the inner integral is with respect to

x

(keeping

y

fixed), while the outer integral is with respect to

y .

🔗

If instead

D

can be written as:

D = {(x, y) \in R^{2} | y \in [c, d], u (y) \leq x \leq v (y)},

🔗

we say that

D

y

-supported (or of type II). The double integral is then the iterated integral:

\iint_{D} f d A = \int_{c}^{d} \int_{u (y)}^{v (y)} f d x d y,

🔗

with the inner integral being with respect to

y

(keeping

x

fixed), and the outer integral with respect to

y .

🔗

Note that rectangular regions are particular cases of both

x

-supported and

y

-supported regions. If a region

D

is either

x

-supported or

y

-supported, we say that it is recursively supported. Most of the regions that we will deal with will be either recursively supported regions, or regions that can be expressed as unions of recursively supported regions.

🔗

Example 5.3.3. Integral of a two-form over a rectangular region with canonical orientation.

Consider the two-form $ω = x y d x \land d y$ on $R^{2},$ and the closed bounded region

D = {(x, y) \in R^{2} | 0 \leq x \leq 2, - 1 \leq y \leq 3},

equipped with the canonical orientation. Then

\begin{aligned} \int_{D_{+}} ω = & \iint_{D} x y d A \\ = & \int_{- 1}^{3} \int_{0}^{2} x y d x d y \\ = & \int_{- 1}^{3} y {[\frac{x^{2}}{2}]}_{x = 0}^{x = 2} d y \\ = & 2 \int_{- 1}^{3} y d y \\ = & y^{2} |_{- 1}^{3} \\ = & 8. \end{aligned}

To evaluate the double integral, we used the standard procedure for evaluating double integrals over rectangular regions as iterated integrals, with the inner integral being with respect to $x$ (keeping $y$ constant), and the outer integral being with respect to $y .$

🔗

Example 5.3.4. Integral of a two-form over an $x$ -supported (or type I) region with canonical orientation.

Consider the two-form $ω = x e^{y} d x \land d y,$ and the region

D = {(x, y) \in R^{2} | x \in [1, 2], \ln (x) \leq y \leq \ln (2 x)} .

$D$ is an $x$ -supported region. The integral then reads:

\begin{aligned} \int_{D_{+}} ω = & \int_{1}^{2} \int_{\ln (x)}^{\ln (2 x)} x e^{y} d y d x \\ = & \int_{1}^{2} x {[e^{y}]}_{\ln (x)}^{\ln (2 x)} d x \\ = & \int_{1}^{2} (x e^{\ln (2 x)} - x e^{\ln (x)}) d x \\ = & \int_{1}^{2} (2 x^{2} - x^{2}) d x \\ = & \int_{1}^{2} x^{2} d x \\ = & \frac{8}{3} - \frac{1}{3} \\ = & \frac{7}{3} . \end{aligned}

🔗

Remark 5.3.5.

It is worth pointing out here that Definition 5.3.1 is actually quite subtle. We defined the integral of the two-form $ω = f d x \land d y$ over $D_{+}$ as

\int_{D_{+}} f d x \land d y = \iint_{D} f d A,

where the right-hand-side is the standard double integral of a function in calculus. The subtelty is that the right-hand-side is not an oriented integral, while the left-hand-side is. Indeed, suppose for simplicity that $D = [a, b] \times [c, d]$ is a rectangular region, as in Example 5.3.3. Then, we can interpret the right-hand-side as an iterated integral:

\iint_{D} f d A = \int_{c}^{d} \int_{a}^{b} f d x d y .

But then, by Fubini's theorem, we know that we can exchange the order of integration without issue. That is,

\iint_{D} f d A = \int_{c}^{d} \int_{a}^{b} f d x d y = \int_{a}^{b} \int_{c}^{d} f d y d x .

At first sight, this may appear problematic, as one could be tempted to reinterpret the last integral as

\int_{D_{+}} f d y \land d x,

but since $d x \land d y = - d y \land d x,$ this would be minus the integral we started with! But this is incorrect. The subtlety is in the choice of orientation.

The key is that in Definition 5.3.1, we started by choosing coordinates $(x, y)$ on $R^{2},$ and then we wrote the one-form $ω = f d x \land d y$ using the basic two-form $d x \land d y$ in which the differentials $d x$ and $d y$ appear in the same order as the coordinates $(x, y) .$ This is important, as $d y \land d x = - d x \land d y .$ So while we can exchange the order of the iterated integrals once we have written everything in terms of double integrals, when we write the integral in terms of differential forms, we must use the correct choice of basic two-form $d x \land d y$ with the differentials appearing in the same order as the coordinates of $R^{2} .$ That's because integrals of two-forms are oriented, while double integrals of functions are not.

Note that there is nothing special about the variables $x$ and $y .$ We could name the coordinates of $R^{2}$ anything. For instance, if we choose coordinates $(u, v)$ on $R^{2},$ then the integral of a two-form $ω = f d u \land d v$ over a region $D$ is equal to the double integral of $f$ over $D$ (with a positive sign in front) when $D$ is endowed with the canonical orientation described by the ordered basis ${e_{1}, e_{2}},$ with the basis vectors $e_{1} = (1, 0)$ and $e_{2} = (0, 1)$ pointing in the positive directions of the coordinates $u$ and $v$ respectively.²

In a more careful treatment, we would allow to write the two-form

ω

in terms of any basic two-form

α .

We would then define the orientation that is compatible with the basic two-form as corresponding to choices of oriented bases

{u, v}

such that

α (u, v) > 0 .

Our definition would then state that the integral of a two-form written in terms of this basic two-form over a region

D

with the compatible orientation would be given by the double integral of the function over that region, while the integral over the region with opposite orientation would be given by minus the double integral.

🔗

Subsection 5.3.2 Integrals of two-forms over regions in $R^{2}$ are oriented and reparametrization-invariant

🔗

We already mentioned that integrals of two-forms oriented. Let us now be a little more precise, and show that, with our definition, integrals of two-forms are invariant under orientation-preserving reparametrizations, and change sign under orientation-reversing reparametrizations.

🔗

Let us first define what we mean by orientation-preserving and orientation-reversing reparametrizations. We state the definition in

R^{2},

but it naturally generalizes to

R^{n} .

🔗

Definition 5.3.6. Orientation-preserving reparametrizations of regions in $R^{2}$ .

Let $D_{1}, D_{2} \subset R^{2}$ be recursively supported regions,³ and $ϕ : D_{2} \to D_{1}$ a bijective function that can be extended to a $C^{1}$ -function on an open subset $U \subseteq R^{2}$ that contains $D_{2} .$ We assume that $ϕ$ is invertible (except possibly on the boundary of $D_{2}$ ), i.e. the determinant of its Jacobian $det J_{ϕ}$ is non-zero on the interior of $D_{2}$ (recall the definition of the Jacobian in Definition 4.7.5). We say that $ϕ$ is an orientation-preserving reparametrization if $det J_{ϕ} > 0$ for all points in the interior of $D_{2},$ and that it is an orientation-reserving reparametrization if $det J_{ϕ} < 0$ for all points in the interiori of $D_{2} .$

We could extend the statement more generally to closed bounded regions by taking unions of recursively supported regions.

🔗

With this definition, we can now show that our theory of integration for two-forms over regions in

R^{2}

is oriented and reparametrization-invariant, our two guiding principles.

🔗

Lemma 5.3.7. Integrals of two-forms over regions in $R^{2}$ are invariant under orientation-preserving reparametrizations.

Let $D_{1}, D_{2} \subset R^{2}$ be recursively supported regions, and $ϕ$ a reparametrization as in Definition 5.3.6. Let $ω$ be a two-form on an open subset $U \subseteq R^{2}$ that contains $D_{1} .$

If $ϕ$ is orientation-preserving, then
$\int_{D_{2}} ϕ^{*} ω = \int_{D_{1}} ω .$
If $ϕ$ is orientation-reversing, then
$\int_{D_{2}} ϕ^{*} ω = - \int_{D_{1}} ω .$

In other words, the integral is invariant under orientation-preserving reparametrizations, and changes sign under orientation-reversing reparametrizations.

🔗

Proof.

The key is to use Lemma 4.7.7 to calculate $ϕ^{*} ω .$ Since we are pulling back a two-form $ω$ on an open subset $U \subseteq R^{2},$ and that $ϕ : V \to U$ with $V \subseteq R^{2},$ we can apply the result of Lemma 4.7.7. We write $ω = f d x \land d y,$ and $ϕ (u, v) = (x (u, v), y (u, v)) .$ The jacobian of the transformation is

J_{ϕ} = (\begin{matrix} \frac{\partial x}{\partial u} & \frac{\partial x}{\partial v} \\ \frac{\partial y}{\partial u} & \frac{\partial y}{\partial v} \end{matrix}) .

Then Lemma 4.7.7 tells us that

ϕ^{*} ω = f (ϕ (u, v)) (det J_{ϕ}) d u \land d v .

This means that

\int_{D_{2}} ϕ^{*} ω = \int_{D_{2}} f (ϕ (u, v)) (det J_{ϕ}) d u \land d v .

Using our definition of integration in Definition 5.3.1, we know that

\int_{D_{1}} ω = \iint_{D_{1}} f (x, y) d x d y, \int_{D_{2}} ϕ^{*} ω = \iint_{D_{2}} f (ϕ (u, v)) (det J_{ϕ}) d u d v,

where on the right-hand-side of each equation we mean the double integral for the recursively supported regions $D_{1}$ in the $x y$ -plane and $D_{2}$ in the $u v$ -plane.

But recall from your previous calculus course that double integrals satisfy a “transformation formula”, or “change of variables formula”, which is the natural generalization of the substitution formula for definite integrals. The transformation formula states that

\iint_{D_{1}} f (x, y) d x d y = \iint_{D_{2}} f (ϕ (u, v)) | det J_{ϕ} | d u d v .

Note that there is now an absolute value around the determinant of the Jacobian. Thus, what this means is that if our transformation is such that $det J_{ϕ} > 0,$ then $| det J_{ϕ} | = det J_{ϕ},$ and

\int_{D_{1}} ω = \iint_{D_{1}} f (x, y) d x d y = \int_{D_{2}} f (ϕ (u, v)) (det J_{ϕ}) d u \land d v = \int_{D_{2}} ϕ^{*} ω,

while if $det J_{ϕ} < 0,$ then $| det J_{ϕ} | = - det J_{ϕ},$ and

\int_{D_{1}} ω = \iint_{D_{1}} f (x, y) d x d y = - \int_{D_{2}} f (ϕ (u, v)) (det J_{ϕ}) d u \land d v = - \int_{D_{2}} ϕ^{*} ω .

This is the statement of the lemma: integrals of two-forms are oriented and reparametrization-invariant!

🔗

What is particularly nice with the proof of the lemma is that the transformation (or change of variables) formula for double integrals is simply the statement that integrals of two-forms over regions in

R^{2}

are invariant under orientation-preserving reparametrizations! Isn't that cool? It explains why the determinant of the Jacobian appears; it comes from pulling back the two-form under the change of variables.

🔗

The fact that double integrals involve the absolute value of the determinant of the Jacobian, while our integrals do not (and change signs under orientation-reversing reparametrizations), is also interesting. As alluded to above, the reason is that our integrals are oriented, while standard double integrals in calculus are not.

🔗

Example 5.3.8. Area of a disk.

Consider the basic two-form $ω = d x \land d y$ on $R^{2} .$ Let us define the following $x$ -supported domain:

D = {(x, y) \in R^{2} | x \in [- 1, 1], - \sqrt{1 - x^{2}} \leq y \leq \sqrt{1 - x^{2}}} .

It is easy to see that $D$ is a closed disk of radius one centered at the origin. The integral of the basic two-form $ω$ over $D$ should give us the area of the disk, namely $π .$ We calculate:

\begin{aligned} \int_{D} ω = & \iint_{D} d A \\ = & \int_{- 1}^{1} \int_{- \sqrt{1 - x^{2}}}^{\sqrt{1 - x^{2}}} d y d x \\ = & \int_{- 1}^{1} (\sqrt{1 - x^{2}} + \sqrt{1 - x^{2}}) d x \\ = & 2 \int_{- 1}^{1} \sqrt{1 - x^{2}} d x . \end{aligned}

To evaluate this integral, we do a trigonometric substitution, $x = \sin (θ) :$

\begin{aligned} 2 \int_{- 1}^{1} \sqrt{1 - x^{2}} d x = & 2 \int_{- π / 2}^{π / 2} \sqrt{1 - \sin^{2} (θ)} \cos (θ) d θ \\ = & 2 \int_{- π / 2}^{π / 2} \cos^{2} (θ) d θ \\ = & \int_{- π / 2}^{π / 2} (1 + \cos (2 θ)) d θ \\ = & (\frac{π}{2} + \frac{π}{2}) + \frac{1}{2} (\sin (π) - \sin (- π)) \\ = & π . \end{aligned}

We could have instead use a change of variables to evaluate this integral: polar coordinates. Define the map $ϕ : R^{2} \to R^{2}$ with

ϕ (r, θ) = (r \cos (θ), r \sin (θ)) .

Then, if we define the region

D_{2} = {(r, θ) \in R^{2} | r \in [0, 1], θ \in [0, 2 π]},

the map $ϕ : D_{2} \to D$ is bijective and invertible in the interior of $D_{2} .$ The determinant of the Jacobian is

det J_{ϕ} = det (\begin{matrix} \cos (θ) & - r \sin (θ) \\ \sin (θ) & r \cos (θ) \end{matrix}) = r \cos^{2} (θ) + r \sin^{2} (θ) = r,

which is positive for all points in the interior of $D_{2} .$ Thus $ϕ$ is an orientation-preserving reparametrization, so the integral of the pullback $ϕ^{*} ω = r d r \land d θ$ over $D_{2}$ should give us $π$ again. Indeed, we get:

\begin{aligned} \int_{D_{2}} ϕ^{*} ω = & \int_{0}^{2 π} \int_{0}^{1} (det J_{ϕ}) d r d θ \\ = & \int_{0}^{2 π} \int_{0}^{1} r d r d θ \\ = & \frac{1}{2} \int_{0}^{2 π} d θ \\ = & π . \end{aligned}

Notice how easier the integral was! That's of course because polar coordinates are well suited for evaluating integrals over regions that have circular symmetry.

🔗

Exercises 5.3.3 Exercises

🔗

1.

Evaluate the integral of the two-form $ω = \frac{1}{(1 + x + y)^{2}} d x \land d y$ over the rectangular region

D = {(x, y) \in R^{2} | x \in [1, 2], y \in [2, 3]}

with canonical orientation.

Solution.

By definition of the integral, we have:

\begin{aligned} \int_{D} ω = & \int_{D} \frac{1}{(1 + x + y)^{2}} d x \land d y \\ = & \int_{2}^{3} \int_{1}^{2} \frac{1}{(1 + x + y)^{2}} d x d y \\ = & \int_{2}^{3} {[- \frac{1}{1 + x + y}]}_{x = 1}^{x = 2} d y \\ = & \int_{2}^{3} (\frac{1}{2 + y} - \frac{1}{3 + y}) d y \\ = & {[\ln (2 + y) - \ln (3 + y)]}_{y = 2}^{y = 3} \\ = & \ln (5) - \ln (6) - \ln (4) + \ln (5) \\ = & \ln (\frac{25}{24}) . \end{aligned}

🔗

2.

Evaluate the integral of the two-form $ω = \frac{\ln (y)}{x y} d x \land d y$ over the rectangular region

D = {(x, y) \in R^{2} | x \in [1, 4], y \in [1, 5]}

with clockwise orientation.

Solution.

By definition of the integral, we have (we add a minus sign since we are evaluating the integral with clockwise orientation):

\begin{aligned} \int_{D} ω = & - \int_{D} \frac{\ln (y)}{x y} d x \land d y \\ = & - \int_{1}^{5} \int_{1}^{4} \frac{\ln (y)}{x y} d x d y \\ = & - \int_{1}^{5} \frac{\ln (y)}{y} {[\ln (x)]}_{x = 1}^{x = 4} d y \\ = & - \ln (4) \int_{1}^{5} \frac{\ln (y)}{y} d y . \end{aligned}

To evaluate the remaining definite integral, we do a substitution $u = \ln (y),$ $d u = \frac{1}{y} d y,$ and $y = 1$ goes to $u = \ln (1) = 0,$ while $y = 5$ goes to $u = \ln (5) .$ We get:

\begin{aligned} \int_{D} ω = & - \ln (4) \int_{0}^{\ln (5)} u d u \\ = & - \ln (4) {[\frac{u^{2}}{2}]}_{u = 0}^{u = \ln (5)} \\ = & - \frac{\ln (4) (\ln (5))^{2}}{2} . \end{aligned}

🔗

3.

Evaluate the integral of the two-form $ω = \cos (y^{3}) d x \land d y$ over the region $D$ bounded by the parabola $x = y^{2}$ and the lines $x = 0,$ $y = 0$ and $y = 1,$ with canonical orientation.

Solution.

We first describe the region explicitly. It is shown in the figure below: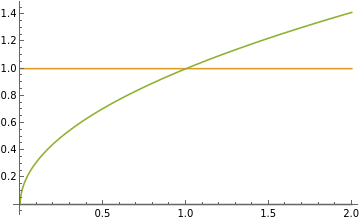

We can describe this region as an

x

-supported or

y

-supported region. If we write it as a

y

-supported region, we would write

0 \leq y \leq 1,

and

0 \leq x \leq y^{2} .

Thus

D = {(x, y) \in R^{2} | y \in [0, 1], 0 \leq x \leq y^{2}} .

If we write it as an $x$ -supported region, we would write $0 \leq x \leq 1,$ and $\sqrt{x} \leq y \leq 1,$ that is,

D = {(x, y) \in R^{2} | x \in [0, 1], \sqrt{x} \leq y \leq 1} .

Which of the two descriptions should we choose? If we use the second description ( $x$ -supported), we first need to integrate in $y .$ But the function that we have to integrate is $\cos (y^{3}),$ which has no elementary antiderivative. So this is problematic. We will not run into this problem if we use the first description ( $y$ -supported); with this description, we first integrate in $x,$ which is fine. And the next integral in $y$ will then be easy, as we will see.

So we use the first description of the region as $x$ -supported. The integral then becomes

\begin{aligned} \int_{D} ω = & \int_{D} \cos (y^{3}) d x \land d y \\ = & \int_{0}^{1} \int_{0}^{y^{2}} \cos (y^{3}) d x d y \\ = & \int_{0}^{1} \cos (y^{3}) {[x]}_{x = 0}^{x = y^{2}} d y \\ = & \int_{0}^{1} y^{2} \cos (y^{3}) d y . \end{aligned}

To evaluate the remaining definite integral, we do the substitution $u = y^{3},$ $d u = 3 y^{2} d y .$ Then $y = 0$ becomes $u = 0,$ and $y = 1$ becomes $u = 1 .$ We get:

\begin{aligned} \int_{D} ω = & \frac{1}{3} \int_{0}^{1} \cos (u) d u \\ = & \frac{1}{3} \sin (u) |_{u = 0}^{u = 1} \\ = & \frac{1}{3} \sin (1) . \end{aligned}

🔗

4.

Consider the two-form $ω = e^{(x^{2} + y^{2})^{2}} d x \land d y,$ and let $D$ be the disk of radius one with counterclockwise orientation. Show that

\int_{D} ω = 2 π \int_{0}^{1} r e^{r^{4}} d r .

Solution.

To show this, we change coordinates from Cartesian coordinates to polar coordinates. We define the function $ϕ : D_{2} \to D,$ with

ϕ (r, θ) = (r \cos (θ), r \sin (θ)),

and

D_{2} = {(r, θ) \in R^{2} | r \in [0, 1], θ \in [0, 2 π]} .

It maps the rectangular region $D_{2}$ to the unit disk $D .$ The determinant of the Jacobian of $ϕ$ is

\begin{aligned} det J_{ϕ} = & det (\begin{array}{c} \frac{\partial x}{\partial r} & \frac{\partial x}{\partial θ} \\ \frac{\partial y}{\partial r} & \frac{\partial y}{\partial θ} \end{array}) \\ = & det (\begin{array}{c} \cos (θ) & - r \sin (θ) \\ \sin (θ) & r \cos (θ) \end{array}) \\ = & r . \end{aligned}

As $r \in [0, 1],$ this is positive on the interior of $D_{2},$ and thus we know that the integral will be invariant under pullback, that is,

\int_{D_{2}} ϕ^{*} ω = \int_{D} ω .

We then calculate the pullback two-form $ϕ^{*} ω :$

\begin{aligned} ϕ^{*} ω = & e^{r^{4}} (det J_{ϕ}) d r \land d θ \\ = & r e^{r^{4}} d r \land d θ . \end{aligned}

Therefore,

\begin{aligned} \int_{D} ω = & \int_{D_{2}} r e^{r^{4}} d r \land d θ \\ = & \int_{0}^{1} \int_{0}^{2 π} r e^{r^{4}} d θ d r \\ = & \int_{0}^{1} r e^{r^{4}} {[θ]}_{θ = 0}^{θ = 2 π} d r \\ = & 2 π \int_{0}^{1} r e^{r^{4}} d r . \end{aligned}

🔗

5.

Consider the two-form $ω = x y d x \land d y,$ and let $D$ be the region bounded by the four curves $y = \frac{1}{x},$ $y = \frac{4}{x},$ $y = x$ and $y = 4 x,$ with canonical orientation. Evaluate the integral of $ω$ over $D$ using the change of variables

(x, y) = (\frac{u}{v}, v) .

Solution.

The region $D$ is shown in the figure below:

We could evaluate the integral of

ω

over

D

by splitting the region

D

into two sub-regions, and then realizing these sub-regions as

x

-supported or

y

-supported. Or, we can do a change of variables, as specified in the question.

We consider the change of variables $ϕ : D_{2} \to D$ with

ϕ (u, v) = (\frac{u}{v}, v) .

What is the domain $D_{2}$ in the $(u, v)$ -plane such that $ϕ (D_{2}) = D ?$ In the variables $u$ and $v,$ the four curves $y = 1 / x,$ $y = 4 / x,$ $y = x$ and $y = 4 x$ become

v = \frac{v}{u}, v = \frac{4 v}{u},, v = \frac{u}{v}, v = 4 \frac{u}{v} .

Those four bounding equations can be rewritten as

u = 1, u = 4, v = \sqrt{u}, v = 2 \sqrt{u} .

Here we used the fact that $v$ is positive, since $y = v$ is positive. So we can describe the region $D_{2}$ in the $(u, v)$ -plane as the $v$ -supported region

D_{2} = {(u, v) \in R^{2} | u \in [1, 4], \sqrt{u} \leq v \leq 2 \sqrt{u}} .

This region is shown in the figure below: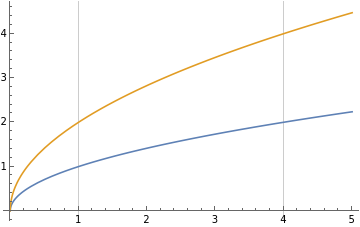

Next, we calculate the determinant of the Jacobian of $ϕ .$ We get:

\begin{aligned} det J_{ϕ} = & det (\begin{array}{c} \frac{\partial x}{\partial u} & \frac{\partial x}{\partial v} \\ \frac{\partial y}{\partial u} & \frac{\partial y}{\partial v} \end{array}) \\ = & det (\begin{array}{c} \frac{1}{v} & - \frac{u}{v^{2}} \\ 0 & 1 \end{array}) \\ = & \frac{1}{v} . \end{aligned}

As $v > 0$ on $D_{2},$ the determinant of the Jacobian is positive on $D_{2} .$ So we know that the integral is invariant under pullback:

\int_{D} ω = \int_{D_{2}} ϕ^{*} ω .

The pullback is:

\begin{aligned} ϕ^{*} ω = & u (det J_{ϕ}) d u \land d v \\ = & \frac{u}{v} d u \land d v . \end{aligned}

We then integrate:

\begin{aligned} \int_{D_{2}} ϕ^{*} ω = & \int_{D_{2}} \frac{u}{v} d u \land d v \\ = & \int_{1}^{4} \int_{\sqrt{u}}^{2 \sqrt{u}} \frac{u}{v} d v d u \\ = & \int_{1}^{4} u {[\ln (v)]}_{v = \sqrt{u}}^{v = 2 \sqrt{u}} d u \\ = & \int_{1}^{4} u (\ln (2 \sqrt{u}) - \ln (\sqrt{u})) d u \\ = & \ln (2) \int_{1}^{4} u d u \\ = & \ln (2) (\frac{16}{2} - \frac{1}{2}) \\ = & \frac{15 \ln (2)}{2} . \end{aligned}

For fun, let us show that we would get the same thing by evaluating the integral of $ω = x y d x \land d y$ directly by splitting the region into two recursively supported sub-regions. Looking at the graph in Figure 5.3.10, one choice is to split $D$ into the two $x$ -supported regions $D_{1}$ and $D_{2},$ with

\begin{aligned} D_{1} = & {(x, y) \in R^{2} | x \in [1 / 2, 1], 1 / x \leq y \leq 4 x}, \\ D_{2} = & {(x, y) \in R^{2} | x \in [1, 2], x \leq y \leq 4 / x} . \end{aligned}

We can then evaluate both integrals separately and add them up to get the result. For $D_{1},$ we calculate:

\begin{aligned} \int_{D_{1}} ω = & \int_{1 / 2}^{1} \int_{1 / x}^{4 x} x y d y d x \\ = & \int_{1 / 2}^{1} x {[\frac{y^{2}}{2}]}_{y = 1 / x}^{y = 4 x} d x \\ = & \int_{1 / 2}^{1} x (8 x^{2} - \frac{1}{2 x^{2}}) d x \\ = & {[2 x^{4} - \frac{1}{2} \ln (x)]}_{x = 1 / 2}^{x = 1} \\ = & \frac{15}{8} - \frac{1}{2} \ln (2) . \end{aligned}

As for $D_{2},$ we get:

\begin{aligned} \int_{D_{2}} ω = & \int_{1}^{2} \int_{x}^{4 / x} x y d y d x \\ = & \int_{1}^{1} x {[\frac{y^{2}}{2}]}_{y = x}^{y = 4 / x} d x \\ = & \int_{1}^{1} x (\frac{8}{x^{2}} - \frac{x^{2}}{2}) d x \\ = & {[8 \ln (x) - \frac{x^{4}}{8} \ln (x)]}_{x = 1}^{x = 2} \\ = & 8 \ln (2) - \frac{15}{8} . \end{aligned}

Adding those two integrals, we get:

\begin{aligned} \int_{D} ω = & \int_{D_{1}} ω + \int_{D_{2}} ω \\ = & \frac{15}{8} - \frac{1}{2} \ln (2) + 8 \ln (2) - \frac{15}{8} \\ = & \frac{15 \ln (2)}{2} . \end{aligned}

This is the same answer that we obtained previously via our change of variables. Great!

Section 5.3 Integrating a two-form over a region in R2

Objectives

Subsection 5.3.1 The integral of a two-form over an oriented closed bounded region in R2

Definition 5.3.1. Integral of a two-form over an oriented closed bounded region in R2.

Remark 5.3.2.

Example 5.3.3. Integral of a two-form over a rectangular region with canonical orientation.

Example 5.3.4. Integral of a two-form over an x-supported (or type I) region with canonical orientation.

Remark 5.3.5.

Subsection 5.3.2 Integrals of two-forms over regions in R2 are oriented and reparametrization-invariant

Definition 5.3.6. Orientation-preserving reparametrizations of regions in R2.

Lemma 5.3.7. Integrals of two-forms over regions in R2 are invariant under orientation-preserving reparametrizations.

Proof.

Example 5.3.8. Area of a disk.

Exercises 5.3.3 Exercises

1.

2.

3.

4.

5.

Section 5.3 Integrating a two-form over a region in $R^{2}$

Subsection 5.3.1 The integral of a two-form over an oriented closed bounded region in $R^{2}$

Definition 5.3.1. Integral of a two-form over an oriented closed bounded region in $R^{2}$ .

Example 5.3.4. Integral of a two-form over an $x$ -supported (or type I) region with canonical orientation.

Subsection 5.3.2 Integrals of two-forms over regions in $R^{2}$ are oriented and reparametrization-invariant

Definition 5.3.6. Orientation-preserving reparametrizations of regions in $R^{2}$ .

Lemma 5.3.7. Integrals of two-forms over regions in $R^{2}$ are invariant under orientation-preserving reparametrizations.