Curvature, Riemann and Ricci tensors, Ricci scalar

Covariant derivative in general is not commutative, 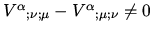${V^{\alpha}}_{; \nu ; \mu} - {V^{\alpha}}_{; \mu ; \nu} \ne 0$. Namely

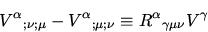$${V^{\alpha}}_{; \nu ; \mu} - {V^{\alpha}}_{; \mu ; \nu} \equiv {R^{\alpha}}_{\gamma\mu\nu} V^{\gamma}$$ (16)

defines Riemann tensor 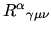${R^{\alpha}}_{\gamma\mu\nu}$ which gives invariant measure of the curvature of the space. The space is flat if ${R^{\alpha}}_{\gamma\mu\nu} = 0$.

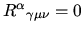Riemann tensor ${R^{\alpha}}_{\gamma\mu\nu}$

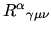
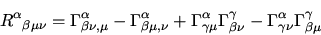$${R^{\alpha}}_{\beta\mu\nu} = \Gamma^{\alpha}_{\beta\nu , \mu... ...a\nu} - \Gamma^{\alpha}_{\gamma\nu} \Gamma^{\gamma}_{\beta\mu}$$ (17)

Ricci tensor $R_{\alpha\beta}$

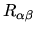
is the contraction of the Riemann tensor

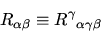$$R_{\alpha\beta} \equiv {R^{\gamma}}_{\alpha\gamma\beta}$$ (18)

Ricci scalar $R$

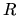
is the further contraction

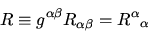$$R \equiv g^{\alpha\beta} R_{\alpha\beta} = {R^\alpha}_{\alpha}$$ (19)