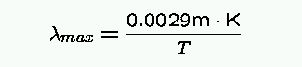Lecture 4: Blackbody Radiation

Thermal Radiation and Blackbodies

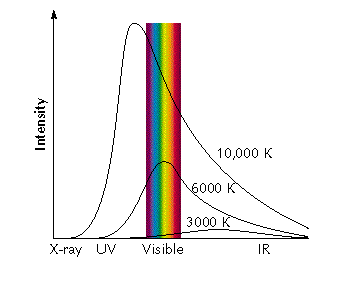
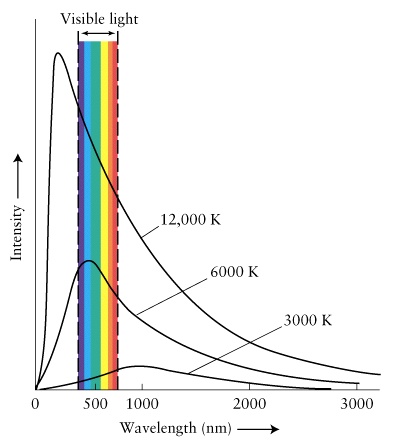
Any object with temperature T > 0 emits EM waves ( radiation ) at all wavelengths. If the object is a perfect absorber, it will not reflect any light. Call this a blackbody. A perfect absorber re-emits all light incident on it. The emitted light has a special spectrum called a blackbody spectrum. Spectrum is the intensity of the line as the function of wavelength Blackbody spectrum is continous and only depends on the surface temperature of the object.

The Sun radiation is almost blackbody

Plot of Intensity of Blackbody radiation versus wavelength for T = 5,000 K:

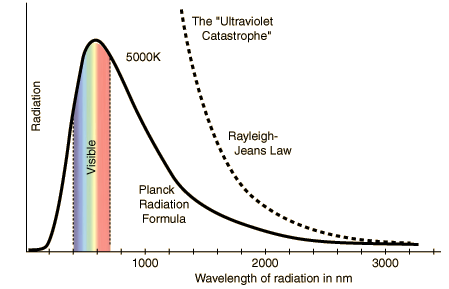
Planck's Curve Long wavelengths (classical Rayleigh-Jeans Law ) Short Wavelength (quantum effects) Detailed discussion of the Planck's curve

Properties of the Blackbody Spectrum

• Shape of the blackbody curve is the same for all temperatures.

• As T increases, the intensity of light at all wavelengths increases.

• The wavelength with the brightest light is denoted   &lambda_max

• As T increase this peak wavelength becomes shorter in inverse proportion to the temperature ( Wien's Law ):
  

The Colour of Stars

• Stars have spectra which are very close to a blackbody.
• The colour of a star will depend on its temperature.

The Sun's Spectrum The black curve represents the Sun's spectrum. The red curve represents the spectrum of a perfect blackbody with surface temperature T=5800 K. The Sun's spectrum can be approximated by a blackbody spectrum. The peak wavelength for a 5800 K blackbody is at wavelength = 0.0029 / (5.8 x 103) m = (2.9/5.8) x 10-3-3 m = 0.5 x 10-6 m = 500 nm. The peak wavelength is for greenish-yellow light. But the Sun is putting out similar amounts of blue and red light. The overall effect is approximately white light with a yellow tint.

What Colour Will a Star Appear To Have?

Example: A star with surface temperature T = 1.2 x 10⁴K

The peak wavelength for this star is at wavelength = 0.0029 / (1.2 x 104) m = (2.9/1.2) x 10-3-4 m = 2.4 x 10-7 m = 240 nm. The peak wavelength is ultraviolet, which our eyes can't detect. The star emits light in all of the visible range, but emits more blue light than red light. Therefore the star will appear to be a blue-white colour. Our eyes aren't very sensitive to violet light, so the tint will appear to be closer to blue than violet.

Example: A star with surface temperature T = 3x10³K

The peak wavelength for this star is at wavelength = 970 nm. The peak wavelength is in the infrared part of the spectrum. The star emits light in all of the visible range, but emits more red light than blue light. The star will appear to be red.

The Energy Flux of a Blackbody

• As T increases, the intensity of light at all wavelengths increases.

• The Energy Flux of an object is the rate that energy is emitted from a square meter of the object's surface.

• F = Energy Flux

• Units of F are J/(s m²) = W/(m²).
• 1 Watt = 1 Joule/second or W=J/s.

• A blackbody has an energy flux which depends only on its Temperature.
• The formula is ( Stefan's Law ):
  

• The constant "sigma" is called the Stefan-Boltzmann constant and is given by:
  

• The temperature in this equation is the surface temperature of the object! The object might be much hotter deep inside, but this doesn't matter.

The Luminosity of a Blackbody

• The luminosity of a star is the power that it emits.

• Power is the rate that energy is emitted by the star.

• Symbol for luminosity is "L".
• Units for luminosity are Watts = W.

• The luminosity is equal to the Energy Flux times the surface area of the object (if F is constant over the object).
  L = F x A

• A spherical object, such as a star has a surface area, A, given by
  A = 4 &pi R²
  where R is the star's radius.

• If the star is a blackbody, then its power output or luminosity is
  L = 4 &pi R² &sigma T⁴
  
• The luminosity of a star depends both on its temperature and on its size. The larger and hotter it is, the more powerful it will be.