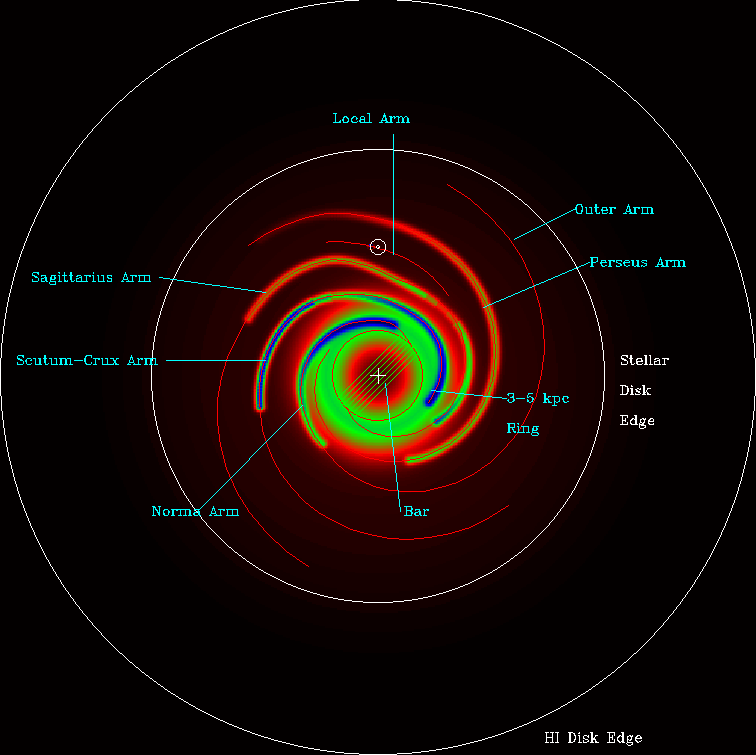
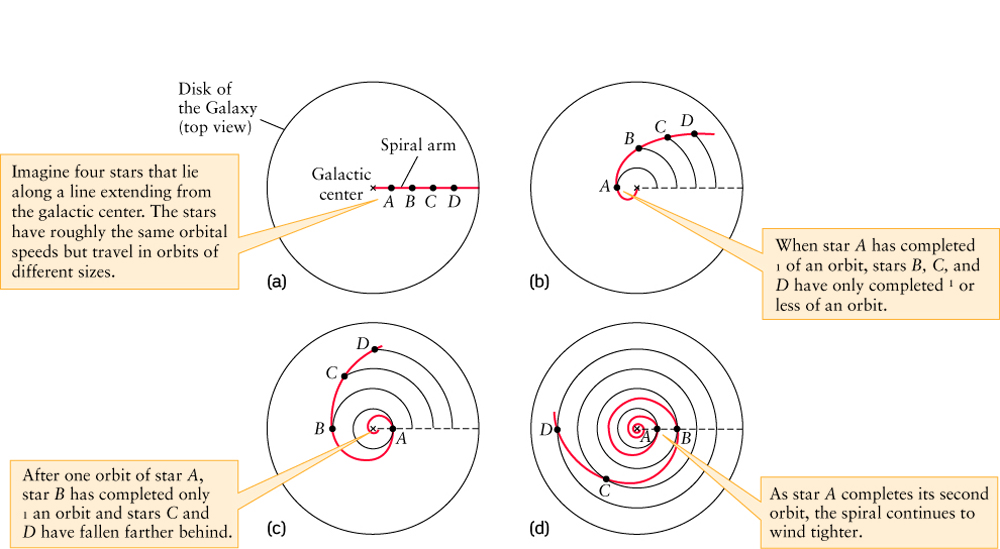
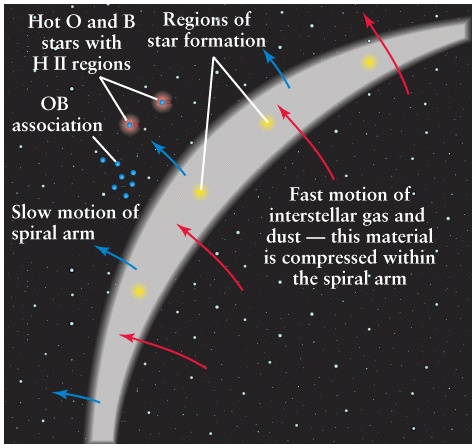
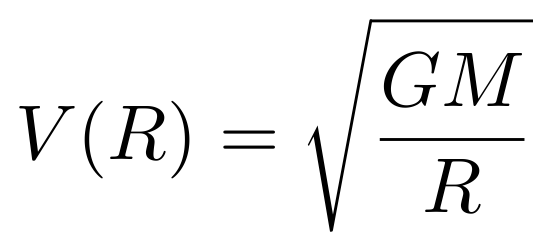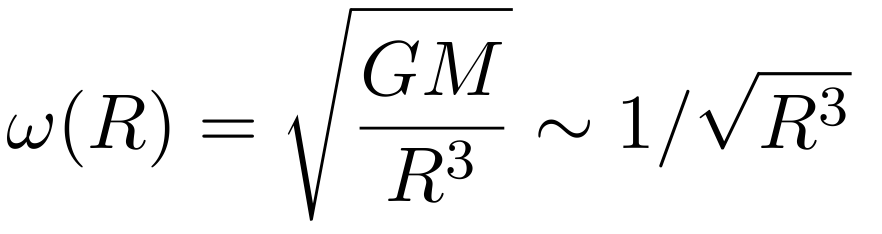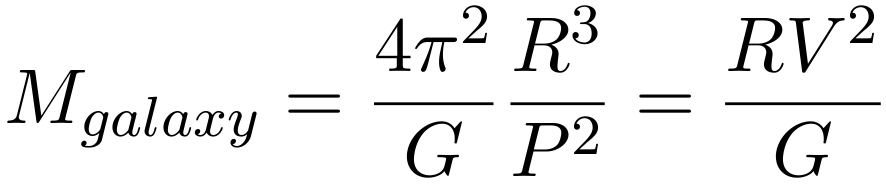The Motion of other Stars
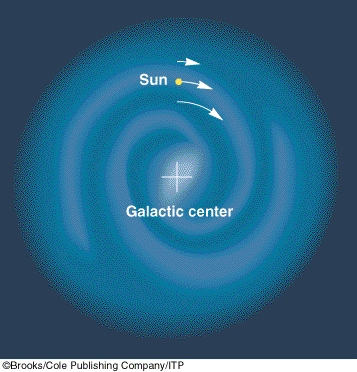
- The motion of stars in the range of 1 kpc to
16 kpc from the galactic centre has been measured.
- The stars move approximately on circular orbits about the
galactic centre along with small peculiar velocities.
- For most of the stars, the velocities range between
200 km/s to 250 km/s.
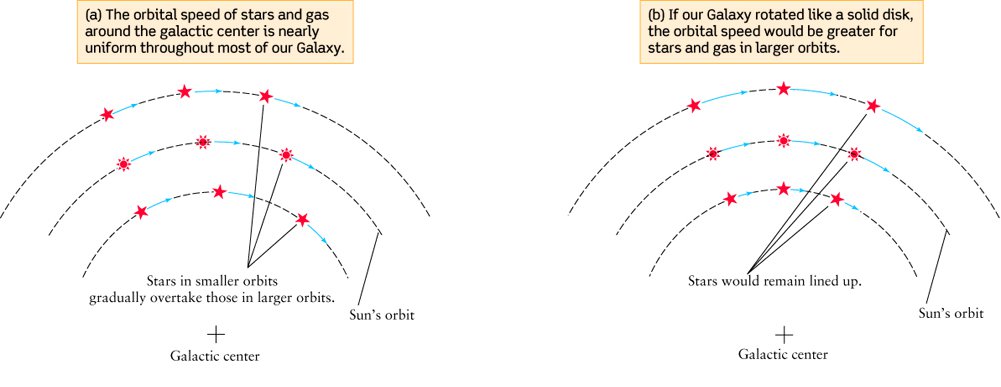
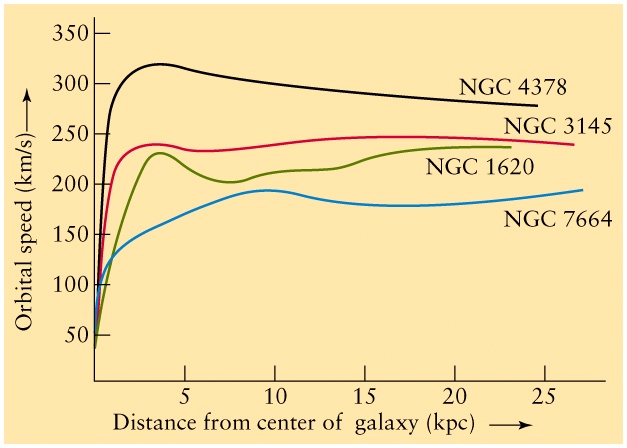
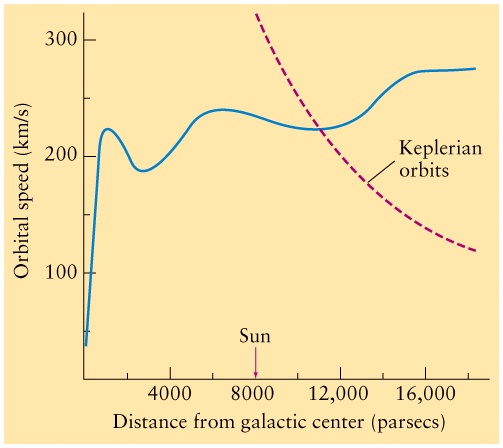
- The plot of velocity versus distance from the centre
of the galaxy is called a rotation curve.
- The most important feature of the rotation curve
is that the velocity of stars far away from the galactic centre
stays at a large value near 220 km/s.
- This is not what was expected, because there is almost no
stars at 16kpc, where we still see 220 km/s rotational velocity.
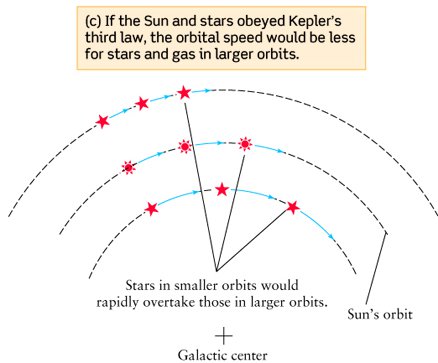
According to Kepler's Laws, the velocity on circular orbit that encompasses
all gravitation mass is
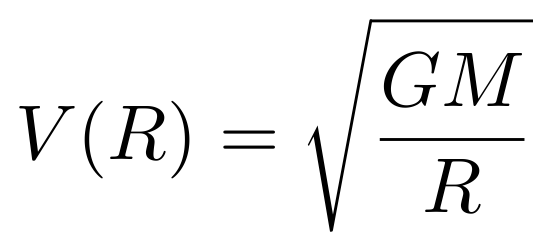 i.e should drop as square root of radius,
i.e should drop as square root of radius, 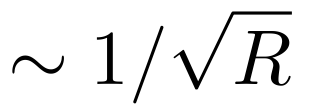
- while angular velocity should drop as
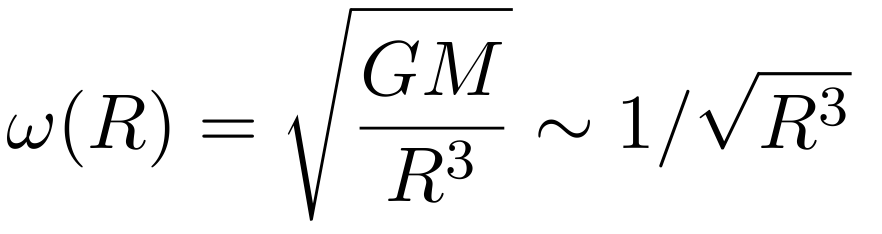
|
|
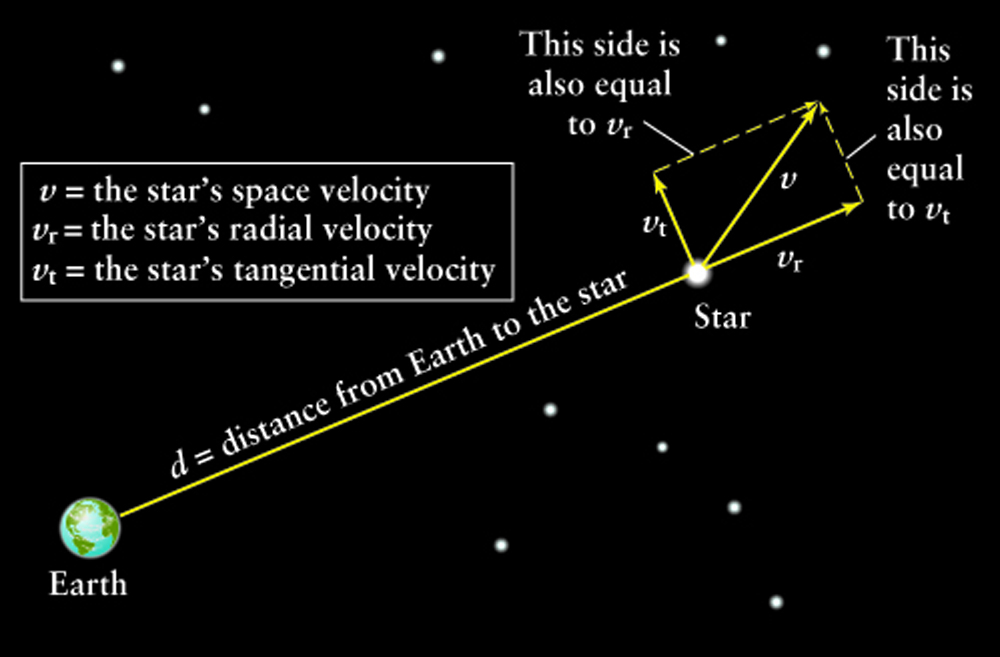 Chapter 17 p 436. Box 17-1.
Chapter 17 p 436. Box 17-1.