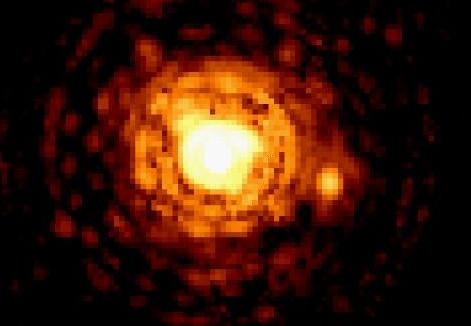
| Hubble Space Telescope photo of Gliese 623, two stars separated by 2 AU. |

|
|
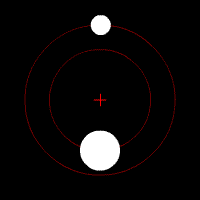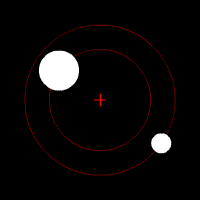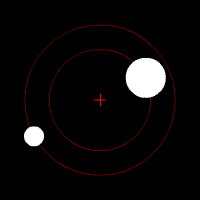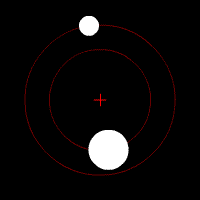
|
|
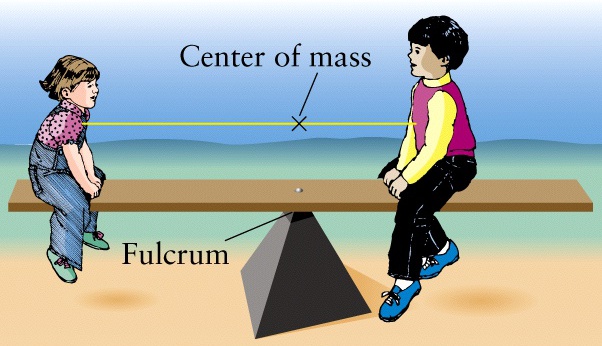
|
An Ellipse
|
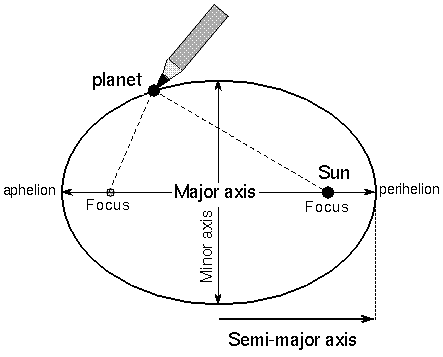
|
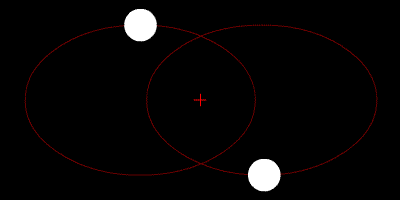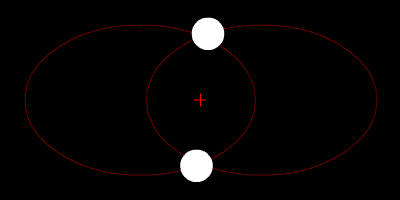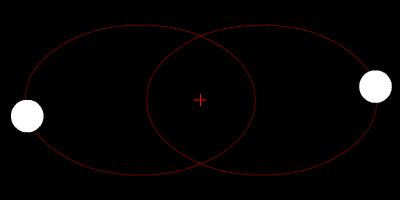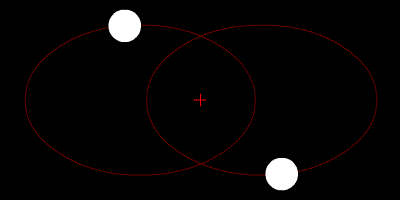
|
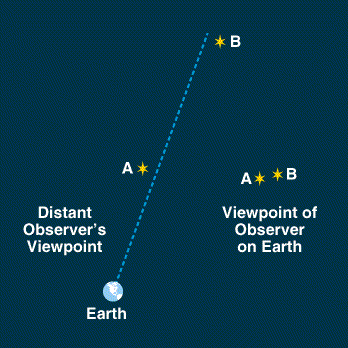 |
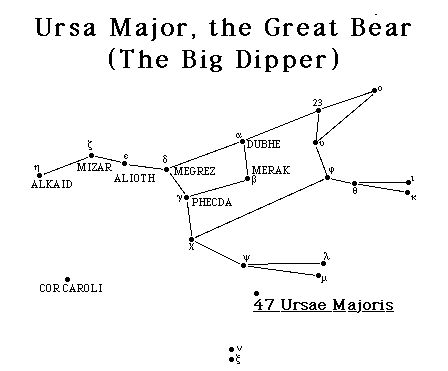 |
 |
 |
 |
| 1908 | 1915 | 1920 |
|
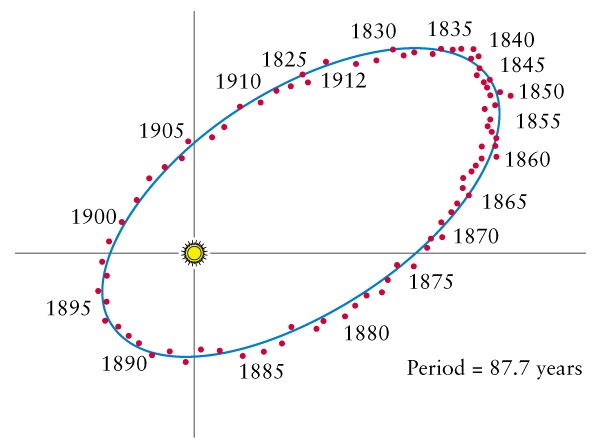
|
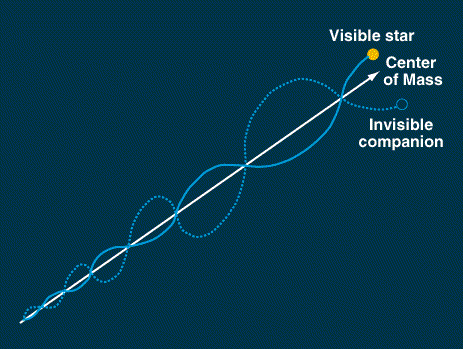
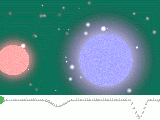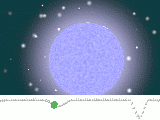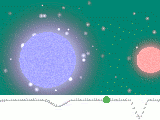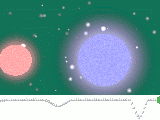
| Star A's light is blueshifted. Star B's light is redshifted. | 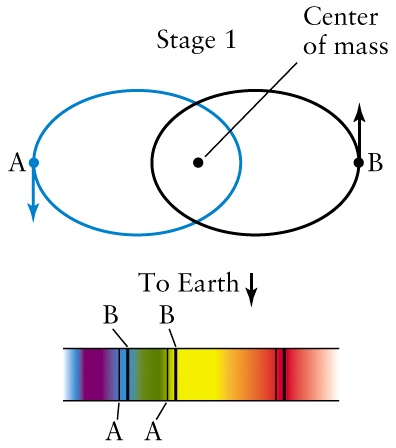
|
| No Doppler shifts occur. | 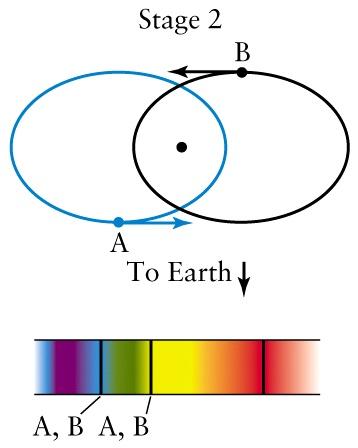
|
| Star A's light is redshifted. Star B's light is blueshifted. | 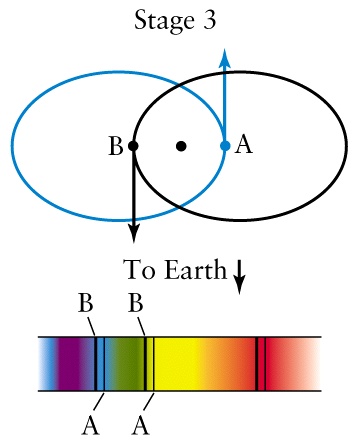
|
| No Doppler shifts occur. | 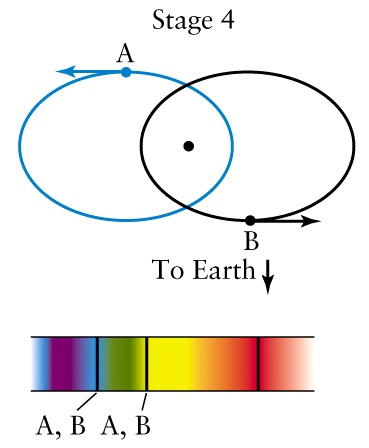 |
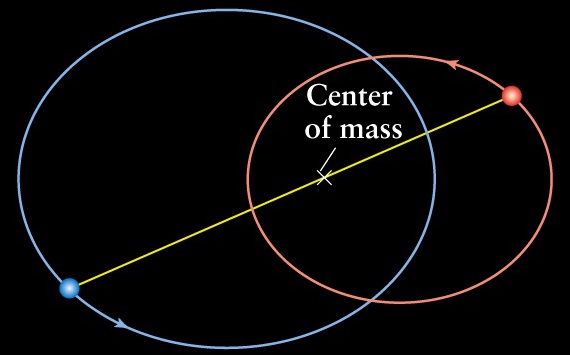
Stellar Velocities in a Spectroscopic Binary
|
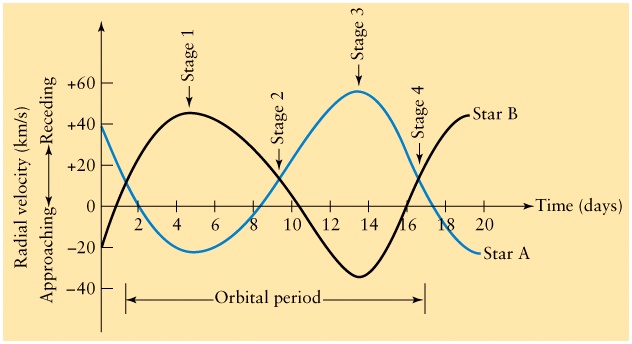
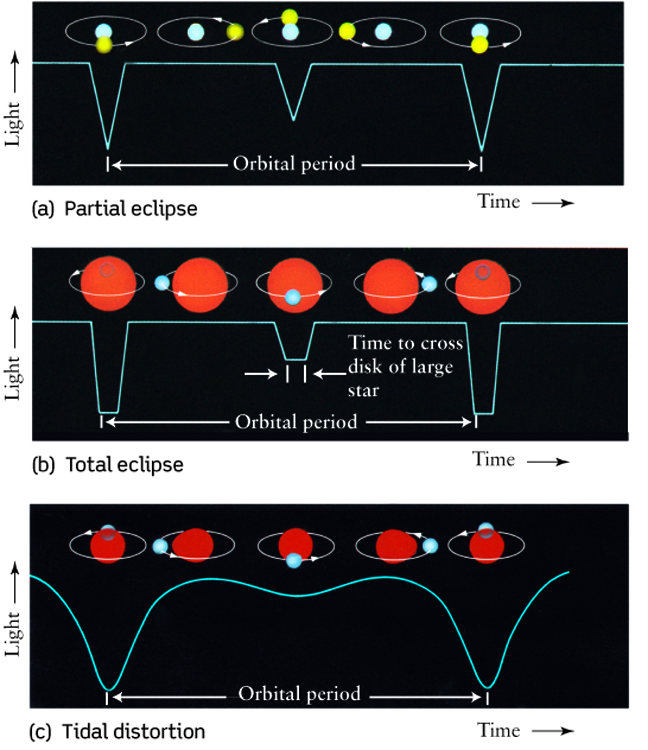
Figure 19-24 |
|
|
|
 |
 |
 |
 |
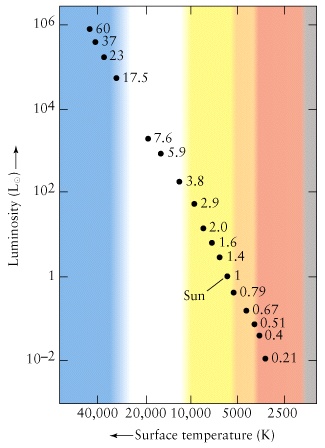 |