Lecture 11: Stars: The Distances and the Brightness

Relating what we see to what happens with the star involves knowledge of distances

• To establish distances to far-away objects we built a distance ladder : we find sizes and distances of local objects, use them to measure distances to next neighbouring ones, use those to go further and further

Distance Ladder:
Earth size &rArr Moon size &rArr Distance to Moon &rArr Distance to the Sun

Eratosthenes (273 - ? BC) determined the size of the Earth.

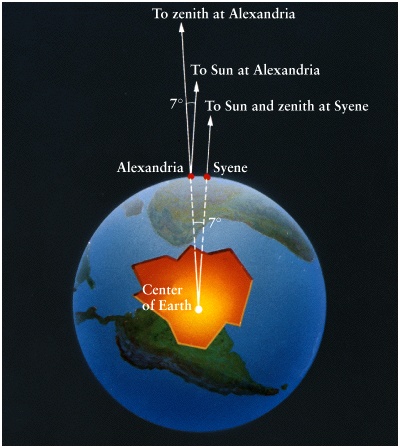
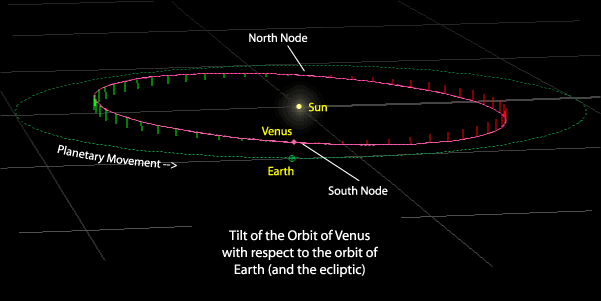
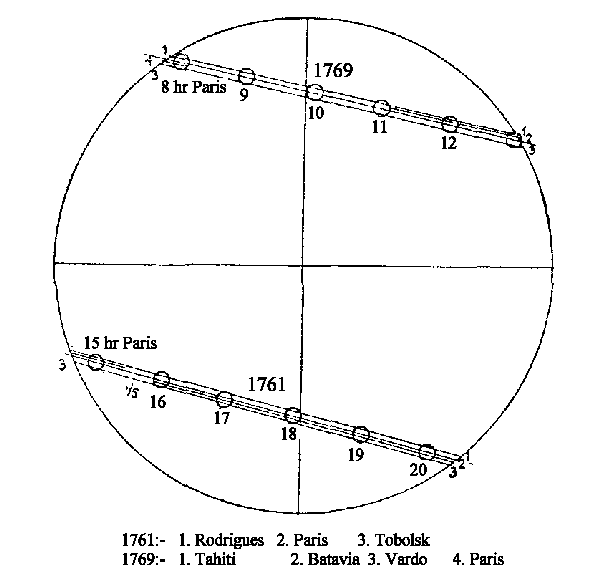
The Ancient Astronomers Aristarchus and Eratosthenes used geometry to find the distances to the Sun and Moon. Alexandria is 780 km due north of the ancient city Syene. On a day when the Sun is at zenith (directly overhead) at noon at Syene, the Sun is 7o away from Zenith at Alexandria. By circular geometry, the circumference of the Earth is C = 780 km x 360/7 = 39,000 km (modern value: 40,074 km !) (The Earth is not exactly a sphere, so this is not exact.)

Aristarchus (310 - 230 BC) determined the Size of the Moon.

Aristarchus determined the distance to the Moon.

The Moon subtends an angle &theta=0.5o (Half of the width of your little finger held out a arm's length.) &theta = Angular diameter of the Moon (observable) D = Diameter of Moon (Aristarchus found it!) To find the distance to the Moon: &theta in radians = 2 &pi x (&theta in degrees)/(360) = 2 &pi x 0.5/360 = 8.7 x 10-3 rad. distance = d = D/(&theta in radians) = D/(8.7 x 10-3) = 3.5 x 103 km / (8.7 x 10-3) = 4.0 x 105 km. (Actual distance is 3.8 x 105 km.)

Modern method for finding distance to Moon:

Aristarchus' Method for finding Distance to the Sun

• Once the distance to the Moon is known, use trigonometry to find the distance to the Sun.
• When Moon is in the first quarter phase, the angle &theta between Sun and Moon (measured from Earth) is not exactly 90 degrees.
• Measure angle, and then

dsun = distance to the Sun dmoon = distance to the Moon dsun = dmoon/cos(&theta)

• Aristarchus measured the angle to be only 87^o and found that the Sun was only 20 x further away from the Moon, but he had the right idea.
• In 1630 Vendelinus used a telescope and measured an angle of 89.75^o which would make the Sun 230 x further away than the Moon, which is a bit better than Aristarchus' measurement.
• The actual angle is 89.853^o
• Therefore the Sun is 390 x further away from us than the Moon.

Using Moon as a step in the ladder is pretty inaccurate, because it is too close !

Distance Ladder: Earth &rArr Venus &rArr Sun

Halley's Method For Finding the Distance to the Sun

• In 1716 Edmond Halley thought about an alternative way to find the distance to the Sun.
• One could easily measure the ratio of the distance between Venus and the Sun (VS) and the distance between the Earth and the Sun (ES) through trigonometry.

VS/ES=sin(&theta)=0.72

• But we do not know VS (nor EV). We need another observation involving VS to exclude it.
  
  Back Next

  ---

Venus Transit

Approximately 2 times a century a straight line would connect the Earth, Venus and the Sun When this occurred, we would see Venus move across the face of the Sun. This is called a Transit of Venus. This happens rarely, because Venus orbit is slightly tilted. Transits come in pairs, separated by 8 years Most recent transit of Venus was June 8, 2004. Next transit of Venus is June 6, 2012.

Halley realized that two observers at different latitudes on the Earth could observe a transit of Venus along different tracks. By comparing their measurements, they could find the physical distance between the tracks on the surface of Sun. And by measuring angular distance between the tracks they can establish the distance to the Sun The data was obtained from the transits of Venus in 1761 and 1769, including Captain Cook's famous voyage to Tahiti.

http://www.nao.rl.ac.uk/nao/transit/

Primer: Physical distance between tracks knowing VS/ES=0.72 and size of Earth

On this diagram, d = distance between the observers on Earth and is a known quantity. We need to find D. Since we have similar triangles, D/LV = d/(LE - LV) . Thus (check the algebra) D = d x (LV/LE)/(1 - LV/LE) = d x 0.72/0.28 = 2.6 x d So the distance D is now known !.

Beyond the Sun: Earth-Sun &rArr neighbouring stars

Hipparchus' (200 - 100 BC) Parallax Method for Finding the Distances to Stars.

Figure 19-2a	Figure 19-b

• Hipparchus' method is named the Method of Parallax
• Suppose you know d_sun = 1 AU.
• If the Earth orbits the Sun, then our position in space changes and the apparent position of a nearby star will change over the course of 6 months.

• Define p = parallax angle = 1/2 the change in angular position of the star.
• parallax angle is measure in arc-seconds.

• Hipparchus did not observe any change in position for any star, so he concluded that the Earth does not move!
• Actual parallax angles are very tiny and difficult to observe.
• First measurement of stellar parallax by Friedrich Bessel in 1835.
• Recent satellite mission named Hipparcos measured the parallax angle for thousands of stars.

• d = distance to the star
• p = parallax angle in arcseconds
• &theta = parallax angle in radians
• &theta = p x 2 &pi / (3600 x 360) = p x 4.848 x 10^-6 rad
• Since the angles are small, the Parallax formula is
  d = AU / &theta = (1.496 x 10¹¹ m) / (p x 4.848 x 10^-6) = 3.086 x 10¹⁶m / p

• Now define a new unit of distance called the parsec.
• 1 parsec = 1 pc = 3.086 x 10¹⁶m = 3.26 light-years.
• parsec is short for parallax-arc-second
• 1 pc is the distance a star is away from us if its parallax angle is 1''.
• Simple formula for distance: d = 1/p where
  • d = distance in units of parsec
  • p = parallax angle in arc-seconds

Back Next

---

Brightness of Light

"brightness" (or intensity) of light is what we measure by our instruments. How bright an object appears to you depends on: the luminosity of the object and the distance between you and the object. Light is emitted from a light bulb or star in all directions. Imagine a spherical wavefront of light moving outwards like an expanding balloon. As the wavefront expands, same energy emitted per second is spread out over a larger surface area.

---

Brightness b of the object at the distance d is the flux (energy per second per unit area) measured at this distance.

---

• A sphere with radius d has surface area
  A = 4 &pi d²
  
• The brightness of a source is luminosity divided by the surface area of the wavefront b = L/A=L/(4 &pi d²) ,
  

• This is called the Inverse Square Law of Light. It's relative form is of most importance
• The observed brightnesses of two objects with intrinsic luminosities L₁ and L₂ that are at distances d₁ and d₂ from the observer, are in the ratio
  
  b₁/b₂ = (L₁/L₂) (d₂/d₁)²
  

Remember:

• The Luminosity of a star is an intrinsic property of the star and is independent of who observes it.

• The brightness of a star depends on how far away the observer is from the star.

Using inverse square law

• If the distance to a star is known, an astronomer can determine the luminosity of the star L= 4 &pi d² b
• If the luminosity is know, the distance to the star can be determined d = (L/(4 &pi b))^1/2

Back

---

---