The gravitational pull of a black hole is
so strong that not even light can escape, but this does not mean that we cannot
ask what is happening in its interior
Black holes:
the inside story

This article appeared in the January 1996 Issue of
Physics World magazine.
This www version of the article was created by Serge Droz.
You can also download a pdf format version
of this article.
A
French translation of this article is also available.
 In 1930 the late
Subrahmanyan
Chandrasekhar showed that the pressure due to the
quantum degeneracy of electrons
could not support a cold star with a mass of more than about 1.4 times
that of the Sun. Is was the first indication that not all stars end their lives
peacefully as
white dwarfs - objects that slowly contract under their own
gravity to the size of the Earth and cool to invisibility. Astrophysicists are
now almost certain that burnt-out stars more than a few times the mass of the
sun collapse to form black holes - objects whose gravitational pull is so strong
that not even light can escape from them.
In 1930 the late
Subrahmanyan
Chandrasekhar showed that the pressure due to the
quantum degeneracy of electrons
could not support a cold star with a mass of more than about 1.4 times
that of the Sun. Is was the first indication that not all stars end their lives
peacefully as
white dwarfs - objects that slowly contract under their own
gravity to the size of the Earth and cool to invisibility. Astrophysicists are
now almost certain that burnt-out stars more than a few times the mass of the
sun collapse to form black holes - objects whose gravitational pull is so strong
that not even light can escape from them.
What happens as the star collapses? As the external gravitational field
settles in the wake of the collapse like a quivering soap bubble, every
irregularity and distinguishing feature is swallowed up or radiated away.
Observers outside the hole see the gravitational field asymptotically
approaching a standard configuration known as the Kerr-Newman field and
characterized by just three numbers: mass, angular momentum and charge. In the
words of John Wheeler: "a black hole has no hair". Chandrasekhar has called them
"the most perfect macroscopic objects in the universe".
Black hole basics
What lurks behind the smooth, hairless facade of
the "event horizon" (the hole's surface)? This is a question that it might be
prudent not even to raise. With black holes only just recently admitted into the
fold, questions of this sort beg to be labeled as airy-fairy fantasy, and anyone
professing to take them seriously as a simpleton, charlatan or crackpot.
Whatever may happen inside the hole, we will never observe it, nor will it
affect anything we can observe. What is more, in 1965
Roger Penrose, then at
Birkbeck College in
London, proved that there must be a singularity within the hole, signalling a
breakdown of all the laws of physics. Moreover, various irregularities swept
inward with the collapse must be expected to grow and accumulate, creating inner
chaos. On the face of it, this hardly seems a fit topic for serious scientists
of sound views.
In fact, the prospects are less bleak than we have painted them because of a
key property of the hole's interior that we have not yet mentioned. Descent into
a black hole is fundamentally a progression in time. Inside the hole, every form
of matter and every causal influence is condemned to fall inwards (i.e. towards
smaller radii). The future is inseparably linked with diminishing radius, so the
radial coordinate, r, becomes time. This means that we are confronting an
evolutionary, not a structural, problem. Moreover, we don't even need a quantum
theory of gravity until space-time is bent on scales of the Planck length
(~10-33 cm). This
is because simple causality prevents our ignorance of the inner, high-curvature
regions from affecting the description of the outer and preceding layers
afforded by today's standard, well established theories.
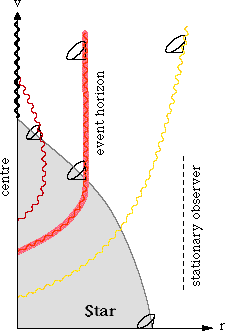
1 The space-time history of the collapse of an uncharged
spherical star. The horizontal axis is radius and the vertical axis is
advanced time, v. In this space-time a photon moving radially inwards would be
represented by a horizontal line (not shown). The wavy lines are photons
traveling radially outwards. As the star collapses, its gravitational pull
increases, and eventually the photons are unable to escape. Photons emitted at
the critical moment, E, marginally fail to escape. They are hold captive by
gravity and mark the "event horizon" or boundary of the hole. Matter and
radiation inside the hole must propagate within the future light-cones shown
(since they cannot move faster than light), and are condemned to fall towards
the central singularity at r=0.
Finally, thanks to the no-hair property and work by
Richard Price,
initial conditions for the evolution are known with precision. This should be
contrasted with the situation in cosmology, where the initial state of the
universe is a matter of pure speculation. In 1972 Price, then at the
California Institute of Technology,
showed that initially - that is, near the event horizon - the gravitational
field has a Kerr-Newman form, perturbed by a tail of gravitational waves
decaying as v-p, where v is
"advanced time" and p > 12. (Advanced time is a time coordinate that stays
fixed for photons propagating radially inwards: in flat space, u = t + r/c,
where c is the speed of light). Because of this rapid decay, the tail has no
significant external effects; but internally, as we shall see, its effect is
critical.
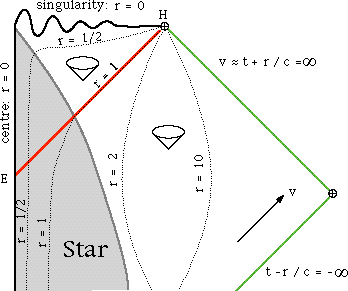
2 The same collapse as shown in Figure 1 in a Penrose map.
Tracks of radially moving
photons are inclined at  45
45  (not shown), and
infinity has been artificially "compactified" by a coordinate transformation
as explained in the text. The Penrose map grossly distorts distances at the
"points" marked by circled crosses (where infinitely many points are crammed
together), and along the "lines" joining these points. Curves of constant
radial coordinate r (in units of the Schwarzschild radius) are shown by dotted
lines; outside the event horizon these lines represent tracks of stationary
observers. The light cones show that, inside the event horizon, all matter and
radiation is condemned to move towards smaller r; outside the event horizon
the light cones show that it is still possible to escape to infinity.
(not shown), and
infinity has been artificially "compactified" by a coordinate transformation
as explained in the text. The Penrose map grossly distorts distances at the
"points" marked by circled crosses (where infinitely many points are crammed
together), and along the "lines" joining these points. Curves of constant
radial coordinate r (in units of the Schwarzschild radius) are shown by dotted
lines; outside the event horizon these lines represent tracks of stationary
observers. The light cones show that, inside the event horizon, all matter and
radiation is condemned to move towards smaller r; outside the event horizon
the light cones show that it is still possible to escape to infinity.
Exploration of the outer layers of a black hole thus emerges as a standard
type of initial-value problem, and so it is possible to make progress. The task
is to integrate the partial differential equations of Einstein's theory forward
in time (and inwards into the hole), beginning from Price's initial conditions
at the event horizon. We have stressed this because it is important to scotch
the notion that what is being attempted is metaphysical or hopelessly
speculative. It is, in fact, no more problematical than following the motion of
a fluid, using Euler's hydrodynamical equations, up to the onset of turbulence
or a shock.
No spin or charge
The simplest black holes are those formed when a
star with zero charge and zero angular momentum collapses. This does not exclude
the possibility that initially the star was ellipsoidal (or cubic). However, to
begin with, let us Iook at the collapse of an exactly spherical star.
Figure 1
depicts the space-time history: the star contracts to radius r=0, where a
singularity is created that extends indefinitely into the future (in the sense
of increasing advanced time v).
The event horizon formed in the collapse can be pictured as a sphere of
imaginary photons, initially expanding but then caught and held stationary (by
the growing surface gravity of the star) at the Schwarzschild radius,
2 G m / c2,
where m is the mass of the hole. For a black hole of six solar masses the
Schwarzschild radius is less than 20 km. On a grander scale, the two billion
solar- mass black hole in the nucleus of the giant galaxy
M87 - whose presence was
recently con firmed by spectrograms taken from the
Hubble Space Telescope
- would swallow up
the orbit of Pluto if relocated in the solar system.
In the space-time of figure 1 the outgoing photons follow bent paths, while
the track of a stationary observer (i.e. constant r) appears as a vertical
straight line. In the curved space of general relativity there are, of course,
no genuinely straight lines; "straightness" is merely a convention of the
mapping. In figure 2 we show the same spherical collapse in a "Penrose map" in
which outgoing and ingoing photon tracks have been "straightened" into lines
running at
 45
45 to the horizontal
(and the stationary-observer tracks are bent). For instance, the event horizon
is now represented by a straight line. At the same time a coordinate
transformation of the form u=tan v' has been applied. This preserves the
directions of photon tracks (u=constant), but compresses the u=
to the horizontal
(and the stationary-observer tracks are bent). For instance, the event horizon
is now represented by a straight line. At the same time a coordinate
transformation of the form u=tan v' has been applied. This preserves the
directions of photon tracks (u=constant), but compresses the u=
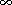 part of the
space-time onto a finite line (u'=
part of the
space-time onto a finite line (u'=
 /2) on the map.
/2) on the map.
The Penrose map brings out the causal structure of space-time. Tracks of
material particles and causal signals moving radially at speeds less than that
of light - are always confined between the north-west and north-east directions
on the map.
If the star is not spherical, then an unproven but plausible conjecture known
as "cosmic censorship" posits that an event horizon should still form. After
some initial agitation, the gravitational field and geometry should settle to a
static, spherical form as v goes to infinity. Indeed, in 1980
Igor Novikov and
Andrei Doroshkevich,
then at the Applied Mathematics Institute in Moscow, argued that this happens
both outside and inside the event horizon. Thus the end-state of any
non-spinning uncharged collapse should be a spherical, Schwarzschild black hole,
perturbed by a dying tail of gravitational waves.
Before admitting spin and charge to this picture, we should point out in
passing that stars and holes bearing electric charge are not of direct
astrophysical interest - any excess charge would be rapidly neutralized by
accretion from the interstellar plasma. However, charged black holes have a role
as models for the realistic black holes formed in a spinning collapse. They
share many of the same features, yet are simpler to deal with because they can
be assumed to be spherical.
Collapse with charge and spin
The event horizon is essentially the
last outpost from which a doomed astronaut falling into the hole can still flash
news to the outside. In the collapses discussed so far, the astronaut can still
receive signals - for example, she will still be able to see the stars in the
night sky - all the way to the singularity at r=0. However, once the smallest
amount of charge or spin is introduced, a new feature - a second, inner horizon
- appears, which seems to alter this picture radically. This horizon marks the
last moment the astronaut can still receive news (figure 3).
The final state of a spherical, charged collapse is known as a
"Reissner-Nordström" black hole. The contracting star passes in turn through the
outer (event) and inner horizons. At this point, gravity at its surface actually
becomes repulsive because of the large amount of electric field energy that is
now located outside the shrunken star and no longer contributing to its
effective internal mass. At event B the star rebounces at a non-zero radius and
reexpands into a new infinite universe. It will continue to pulsate, each time
entering a new universe.
3 Penrose map showing the collapse of a spherical star with
charge. The star contracts within the even horizon, then rebounds at B and
expands into a new universe. An astronaut falling into the hole descends from
the event horizon to the Inner horizon in a time which is finite by her
wristwatch - from a fraction of a second for a solar-mass hole up to eight
hours for the black hole in M87. During this descent she is still able to
receive light signals from the outside, no matter how late these are sent.
Thus she is able to view the entire future of the outer universe before her
own demise when she hits the enormous densities and forces along the inner
horizon.
The prospect of travel to other universes via a black hole sounds like
science fiction, and before we get carried away we should check this picture for
stability. If cosmic censorship holds, inclusion of spin and other
non-sphericities should not prevent an event horizon from forming and the
external field from converging asymptotically to a stationary condition. These
stationary states are uniquely the three-parameter Kerr-Newman geometries, and
they have a lattice-like structure entirely similar to figure 3.
However, there is a snag, first noted by Penrose in 1968. Unlike the simplest
forms of collapse (shown in figures 1 and 2), convergence is now non-uniform
and breaks down completely along the inner horizon. What is the reason for this
instability? Remember that the inner horizon marks the last moment at which our
astronaut can still receive news; but she then gets all of the news. In the few
moments remaining before she plunges through this surface and into the core of
the hole, the entire history of the outer universe will be flashed in fast
motion before her eyes, This compression, or blue shift, has drastic
consequences. The gentle waving of a lady's fan far outside the hole, continued
for long enough, would generate gravitational waves that would hit the poor
astronaut like a pneumatic drill.
In practice, such time-dependent disturbances are unavoidable. The
gravitational-wave tail left by a non- spherical collapse is partially absorbed
by the hole. Moreover, the natural power-law decay of the gravitational
radiation predicted by Price is completely swamped near the inner horizon by the
blue shift of the radiation, which grows as
exp(2 v),
where
v),
where
 is
the "surface gravity" of the inner horizon.
is
the "surface gravity" of the inner horizon.
If our unfortunate astronaut was lucky enough to survive the passage through
this "curtain" of blue-shifted radiation along the inner horizon, figure 3
suggests that she might then pass into to an open, spacious region marked by a
breakdown of predictability. The value of a physical field at an event P in this
region would no longer be uniquely determined by the initial conditions at the
onset of collapse (the surface
 in figure 3),
because of unpredictable influences originating from the singularity at r=O
where the field equations break down. This horizon is known as the "Cauchy
horizon" after the Cauchy initial value problem in mathematical physics.
However, there is no reason to assume that the core of a real black hole will be
anything like the Kerr-Newman or Reissner-Nordström lattices pictured in figure
3.
in figure 3),
because of unpredictable influences originating from the singularity at r=O
where the field equations break down. This horizon is known as the "Cauchy
horizon" after the Cauchy initial value problem in mathematical physics.
However, there is no reason to assume that the core of a real black hole will be
anything like the Kerr-Newman or Reissner-Nordström lattices pictured in figure
3.
This picture of an unstable Cauchy horizon, which becomes singular under
exposure to radiative tails, was established through numerical integrations by
Penrose and Michael Simpson at Birkbeck in 1973, and by several analytical
studies in the following decade. However, this earlier work assumed a fixed
(Reissner-Nordström) background, and did not attempt to estimate the effect of
the blue-shifted radiation on the gravitational field.
The first attempts to take this back-reaction into account were made by William
Hiscock of the University of
Montana in 1981. More representative models were examined by
Eric Poisson
and one of the authors (WI) at the
University of Alberta in 1999, and by
Amos Ori,
then at CalTech, in 1991. To
simplify the mathematics for a first reconnaissance, these early models made
several approximations. It was assumed that rotating (non-spherical) black holes
could be adequately modeled by spherical charged holes, since their horizon
structures are similar. Gravitational (quadrupole) wave tails were modeled by
spherical scalar waves. More general studies by Ori, by
Patrick Brady,
Chris Chambers and John Smith at the University of
Newcastle-upon-Tyne in the UK, and by our group at the University of
Alberta, confirm that these simplified models capture most of the essential
features of the generic case.
The most dramatic of these is an effect that has been dubbed "mass
inflation". The blue-shifted influx due to the gravitational wave tail causes
the local mass function to blow up exponentially near the Cauchy horizon (figure
4). The mass function m(u,v), is the mass inside a given radius. More explicitly,
m(u,v)  C v -p
exp(
C v -p
exp( [u+v]), Where C is
a constant and u is an internal retarded time that increases from -
[u+v]), Where C is
a constant and u is an internal retarded time that increases from -
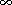 as we move
inwards from the event horizon. (Localized mass is not well defined in general
relativity and it would perhaps be better to speak of the blow-up of local
conformal curvature
as we move
inwards from the event horizon. (Localized mass is not well defined in general
relativity and it would perhaps be better to speak of the blow-up of local
conformal curvature
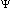 ~ m/r3.)
~ m/r3.)
We hasten to reassure the reader that no trace of this inflation can be
detected externally. News of the drastic change of internal field travels at the
speed of light (as a gravitational wave) and cannot escape from the hole. So
outside observers register a mass no larger than that of the original star.
The singularity along the Cauchy horizon produced by mass inflation appears
quite gross but is actually spread over the surface of the Cauchy horizon.
Although a free-falling object experiences infinite tidal forces at the Cauchy
horizon, these forces do not grow fast enough to deform the object significantly
before it reaches the horizon.
Mechanics of mass inflation
To demystify these phenomena, a simple
mechanical example may help. Consider a concentric pair of thin spherical
shells, of masses mcon and mexp,
contracting and expanding
at the speed of light, and remember
that in Einstein's nonlinear theory, gravitational energy also exerts a
gravitational attraction on matter. The mutual potential energy of the shells
acts as a debit (a binding energy) of order
-G mexpmcon/r
on the gravitational
mass-energy of whichever is the outer shell. When the
shells cross, say at radius r0, this
debit is transferred from the contracting shell to the expanding one, and their
masses change. The exact calculation shows that the new masses,
m'con and
m'exp are
m'con = mcon
(1 - 2 G mexp/c2 r0)-1
m'exp = mexp
(1 - 2 G mcon/c2 r0)
.
The total mass and energy are, of course, conserved. If the encounter takes
place just outside a horizon, the infalling mass can become arbitrarily large.
The total energy (kinetic plus potential)
m'exp c2 is then
negative, which means that the expanding shell is now trapped inside a black
hole. This simple model already provides a fair schematic picture of what
happens near the Cauchy horizon, with the two shells representing streams of
infalling and back-scattered radiation.
Mass inflation is not just a catch-phrase for something of merely formal
significance. If the infalling light were absorbed by a lump of charcoal at the
centre, it would contribute the full value of its inflated mass-energy to the
lump.
Inside knowledge
Our message is that the interior of a generic black
hole is not completely inscrutable: the investigations we have described lead to
a working picture of at least the outer, classical layers of the hole.
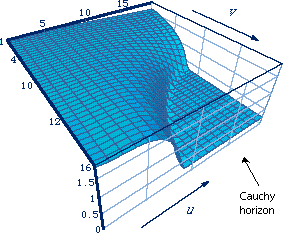
4 Mass inflation near the Cauchy horizon. This shows how
exp(-2 G m / c2 r), plotted
vertically, goes sharply to zero (and hence m approaches infinity
) at the
Cauchy horizon. From numerical integrations by Brady and Smith at Newcastle
University.
The generic picture is not so very different from the simplest pictures we
began with. The one striking new feature is the appearance of a locally mild,
precursory singularity to the strong central singularity. It sits on the Cauchy
horizon, which is a three-dimensional cylinder inside the hole. It extends
indefinitely into the past and contracts towards the future, finally tapering to
the crushing singularity at its future endpoints, represented by C in figure 5.
In effect the Cauchy horizon serves as a bridge, linking the quiescent,
asymptotically hairless, final phases of the hole (at late advanced time) to the
"hairy" crunch near C that is associated with its formation.
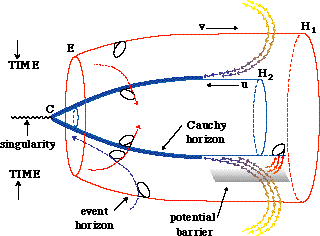
5 The inside of a black hole with one angular variable
suppressed. Inside the hole, increasing time coincides with decreasing radius,
r. Radiation flowing into the hole is partially scattered by a ridge of
curvature midway between the two horizons. The unscattered portion gets
strongly blue-shifted and accumulates along the Cauchy horizon. The scattered
radiation initiates contraction of the Cauchy horizon, thereby catalysing the
inflationary conversion of potential energy into material energy.
Objects tossed into the hole at progressively later advanced times (v) fall
towards the Cauchy horizon at progressively earlier internal retarded times (u).
What happens to these objects when they reach the Cauchy horizon?
We can only speculate on the answer to this question. Our classical models
break down just before the Cauchy horizon because the curvature of space-time
begins to approach the Planck scale and we need a quantum theory of gravity. So
far we have only charted a coastline: we do not yet know whether it heralds a
narrow strip of land or a continent. The most conservative answer would be that
the question is not well posed because, for a real black hole, the Cauchy
horizon never "happens". It is always forestalled - either by evaporation of the
hole or by its merging with other black holes in a cosmological big crunch.
Therefore, the fate of the objects that are suddenly catapulted from near the
Cauchy horizon into the remote future is bound up with the fate of the universe
as a whole.
Further reading
WWW version by S. Droz,
9 February 1996 



 45
45  (not shown), and
infinity has been artificially "compactified" by a coordinate transformation
as explained in the text. The Penrose map grossly distorts distances at the
"points" marked by circled crosses (where infinitely many points are crammed
together), and along the "lines" joining these points. Curves of constant
radial coordinate r (in units of the Schwarzschild radius) are shown by dotted
lines; outside the event horizon these lines represent tracks of stationary
observers. The light cones show that, inside the event horizon, all matter and
radiation is condemned to move towards smaller r; outside the event horizon
the light cones show that it is still possible to escape to infinity.
(not shown), and
infinity has been artificially "compactified" by a coordinate transformation
as explained in the text. The Penrose map grossly distorts distances at the
"points" marked by circled crosses (where infinitely many points are crammed
together), and along the "lines" joining these points. Curves of constant
radial coordinate r (in units of the Schwarzschild radius) are shown by dotted
lines; outside the event horizon these lines represent tracks of stationary
observers. The light cones show that, inside the event horizon, all matter and
radiation is condemned to move towards smaller r; outside the event horizon
the light cones show that it is still possible to escape to infinity.
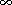 part of the
space-time onto a finite line (u'=
part of the
space-time onto a finite line (u'=
 /2) on the map.
/2) on the map.

 v),
v), in figure 3),
because of unpredictable influences originating from the singularity at r=O
where the field equations break down. This horizon is known as the "Cauchy
horizon" after the Cauchy initial value problem in mathematical physics.
However, there is no reason to assume that the core of a real black hole will be
anything like the Kerr-Newman or Reissner-Nordström lattices pictured in figure
3.
in figure 3),
because of unpredictable influences originating from the singularity at r=O
where the field equations break down. This horizon is known as the "Cauchy
horizon" after the Cauchy initial value problem in mathematical physics.
However, there is no reason to assume that the core of a real black hole will be
anything like the Kerr-Newman or Reissner-Nordström lattices pictured in figure
3.
 C v -p
exp(
C v -p
exp( [u+v]), Where C is
a constant and u is an internal retarded time that increases from -
[u+v]), Where C is
a constant and u is an internal retarded time that increases from -
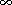 as we move
inwards from the event horizon. (Localized mass is not well defined in general
relativity and it would perhaps be better to speak of the blow-up of local
conformal curvature
as we move
inwards from the event horizon. (Localized mass is not well defined in general
relativity and it would perhaps be better to speak of the blow-up of local
conformal curvature
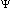 ~ m/r3.)
~ m/r3.)

