Teaching Philosophy
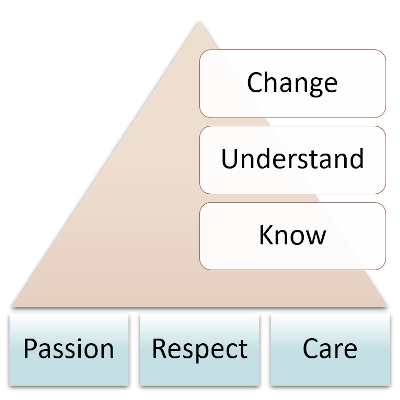
KNOW, UNDERSTAND, and CHANGE. These are the three building blocks that determine my teaching philosophy. The core concept of my teaching philosophy is based on the state of flow. Introduced by M. Csíkszentmihályi, this concept means that flow occurs when a person’s skills are fully involved in solving a challenge that is just about manageable. For me, the flow equals learning. My core goal for every lecture that I teach is to make sure that students learn. To do so, I need to make sure that I provide them challenges that push their capabilities to the limit when they get to the state of flow. To facilitate the state of flow, I put a lot of emphasis on creating a classroom environment of passion, respect, and care. In this case, students are willing to learn the material (know), understand it such that they can change their own thinking and world around them.
Courses
MEC E 539 – Applied Computational Fluid Dynamics
Course Objectives & General Content:Starting from the mathematical preliminaries and brief review of fluid mechanics, we learn fundamental principles of computational fluid dynamics (CFD). Strong emphases are put on understanding of the essential steps in simulations process. We learn how to state the physical problem, formulate mathematical description, discretize equations, generate grid, solve equations, and analyze the results. Strong theoretical foundation are combined with hands-on experience using MATLAB and commercial CFD package STAR-CCM+ to illustrate practical implementations and outline the connection between theory and practice. We do lots of active learning activities that foster the development of engineering skills essential for your future career as an engineer or for graduate program.
Learning Outcomes:By the end of this course, students should be able to:- Read and simplify the governing equations of fluid mechanics
- Select appropriate models for numerical flow analysis
- Carry out numerical simulations using commercial software
- Verify and validate numerical models
- Visualize and critically assess numerical results
MEC E 692 – Fundamentals of Engineering Numerical Analysis
Course Objectives & General Content:Various engineering problems cannot be solved by exact (analytical) methods. In this case, numerical methods can be applied to solve a mathematical problem efficiently. This course is aimed to provide graduate students with a fundamental understanding of the theory behind numerical methods and primarily the application of different numerical algorithms to solve practical engineering tasks. With the abundance of freely available software packages for numerical simulations that include numerous built-in functions, it is crucial to understand how these packages and functions work. The understanding and modification of a given numerical code, the ability to implement a new user-defined function into open-source or commercial software, the extension of capabilities of the existing built-in functions to improve their accuracy and stability are several essential skills that require a strong knowledge of the numerical methods.
Learning Outcomes:By the end of this course, students should be able to:- Apply numerical methods to obtain approximate solutions to mathematical problems (numerical differentiation, integration, interpolation and curve fitting)
- Numerically solve single nonlinear equations, systems of nonlinear equations, systems of linear algebraic equations
- Numerically solve ordinary and partial differential equations (ODEs and PDEs)
- Analyze and evaluate the accuracy of numerical methods
- Implement (program) numerical algorithms into a code
EN PH 131 – Engineering Physics
Course Objectives & General Content:This course covers kinematics and dynamics of particles and system of particles; work and energy principles; linear and angular momentum; energy and momentum conservation; introduction to dynamics of rigid bodies.
Learning Outcomes:By the end of this course, students should be able to:- Describe the kinematics of planar motion (rectilinear and curvilinear) of particles using rectangular and normal/tangential components;
- Draw free body diagrams, kinetic diagrams and apply them to the solution of the problems involving planar motion of particles;
- Apply equations of motion, Newton's Laws, the principles of work and energy, and principle of impulse and momentum to the solution of the problems involving planar motion of particles;
- Describe the kinematics of planar rigid bodies rotating about a fixed axis or rolling without slipping;
- Apply equations of motion for planar rigid bodies rotating about a fixed axis or rolling without slipping.