""" |
expression tree evaluator |
|
Evaluate an expression tree expr in the context of the symbols |
defined in the symtab dictionary. |
|
We define an expression with a grammar |
|
<EXPR> - an expression |
<OP> - an operator '+', '*' |
<NUMBER> - any valid python number |
|
<EXPR> := <CONST_EXPR> | <FORMULA_EXPR> |
<CONST_EXPR> := <NUMBER> |
|
<FORMULA_EXPR> := '(' <EXPR> <OP> <EXPR> ')' |
|
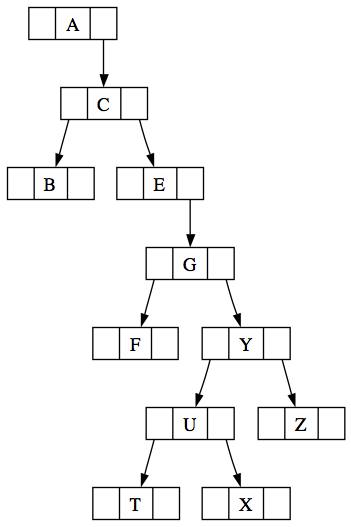
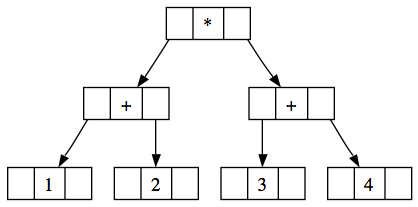
These expressions natually map onto trees |
|
Representing expressions as trees |
|
An expr tree can be a list of the form |
[ value ] |
representing a <CONST_EXPR> |
|
or a list of the form |
[ op, left, right ] |
representing a <FORMULA_EXPR> |
where |
op is '+' or '*' |
left, right are expr |
|
""" |
|
def exp_eval(expr): |
""" |
|
expr_eval(expr) <-- computes the value of expression tree expr |
|
>>> exp_eval( [ ] ) |
'Error: does not compute' |
|
>>> exp_eval( [ 42 ] ) |
42 |
|
>>> exp_eval( [ [ 42 ] ] ) |
|
>>> exp_eval( [ '+', [2], [3] ] ) |
5 |
|
>>> exp_eval( [ '*', [ '+', [1], [2]], ['+', [3], [4]] ] ) |
21 |
|
>>> exp_eval( [ "hello" ] ) |
'hello' |
|
>>> exp_eval( [ '+', [ "hello" ], [ "world"] ] ) |
'helloworld' |
|
>>> exp_eval( [ '*', [ "h" ], [ 3 ] ] ) |
'hhh' |
|
>>> exp_eval( [ '+', [2], ['-', [1], [2]] ] ) |
5 |
|
""" |
|
if len(expr) == 1: |
return expr[0] |
|
if len(expr) == 3: |
op = expr[0] |
lhs = expr[1] |
rhs = expr[2] |
if op == '+': |
return exp_eval(lhs) + exp_eval(rhs) |
if op == '*': |
return exp_eval(lhs) * exp_eval(rhs) |
|
return "Error: I cannot do " + op |
|
return "Error: does not compute" |
|
if __name__ == '__main__': |
import doctest |
doctest.testmod(verbose = 1) |
""" |
expression tree evaluator |
|
Evaluate an expression tree expr in the context of the symbols |
defined in the symtab dictionary. |
|
We define an expression with a grammar |
|
<EXPR> - an expression |
<OP> - an operator '+', '*' |
<NUMBER> - any valid python number |
|
<EXPR> := <CONST_EXPR> | <FORMULA_EXPR> |
<CONST_EXPR> := <NUMBER> |
|
<FORMULA_EXPR> := '(' <EXPR> <OP> <EXPR> ')' |
|
These expressions natually map onto trees |
|
Representing expressions as trees |
|
An expr tree can be a list of the form |
[ value ] |
representing a <CONST_EXPR> |
|
or a list of the form |
[ op, left, right ] |
representing a <FORMULA_EXPR> |
where |
op is '+' or '*' |
left, right are expr |
|
""" |
|
def exp_eval(expr): |
""" |
|
expr_eval(expr) <-- computes the value of expression tree expr |
|
>>> exp_eval( [ ] ) |
'Error: does not compute' |
|
>>> exp_eval( [ 42 ] ) |
42 |
|
>>> exp_eval( [ '+', [2], [3] ] ) |
5 |
|
>>> exp_eval( [ '*', [ '+', [1], [2]], ['+', [3], [4]] ] ) |
21 |
|
It works on things that are not numbers but understand +, * |
|
>>> exp_eval( [ "hello" ] ) |
'hello' |
|
>>> exp_eval( [ '+', [ "hello" ], [ "world"] ] ) |
'helloworld' |
|
>>> exp_eval( [ '*', [ "h" ], [ 3 ] ] ) |
'hhh' |
|
Even on lists! |
|
>>> exp_eval( [ [ 42 ] ] ) |
[42] |
|
>>> exp_eval( [ '+', [ [1] ], [ [2, 3] ] ] ) |
[1, 2, 3] |
|
>>> exp_eval( [ '*', [ [1] ], [ 3 ] ] ) |
[1, 1, 1] |
|
Being Pythonic (not Pythonesque?) |
If lists can be used to structure an expression, the tuples should |
also work. The singleton tuple (1,) is syntactically ugly |
|
>>> exp_eval( ( '*', ( '+', (1,), (2,)), ('+', (3,), (4,)) ) ) |
21 |
|
But we need some more operations |
>>> exp_eval( [ '+', [2], ['-', [1], [2]] ] ) |
5 |
|
""" |
|
val = None |
|
if len(expr) == 1: |
val = expr[0] |
|
elif len(expr) == 3: |
op = expr[0] |
lhs = expr[1] |
rhs = expr[2] |
if op == '+': |
val = exp_eval(lhs) + exp_eval(rhs) |
elif op == '*': |
val = exp_eval(lhs) * exp_eval(rhs) |
else: |
val = "Error: I cannot do " + op |
|
else: |
val = "Error: does not compute" |
|
return val |
|
if __name__ == '__main__': |
import doctest |
doctest.testmod(verbose = 1) |
""" |
expression tree evaluator |
|
Evaluate an expression tree expr in the context of the symbols |
defined in the symtab dictionary. |
|
We define an expression with a grammar |
|
<EXPR> - an expression |
<OP> - an operator '+', '*' |
<NUMBER> - any valid python number |
|
<EXPR> := <CONST_EXPR> | <FORMULA_EXPR> |
<CONST_EXPR> := <NUMBER> |
|
<FORMULA_EXPR> := '(' <EXPR> <OP> <EXPR> ')' |
|
These expressions natually map onto trees |
|
Representing expressions as trees |
|
An expr tree can be a list of the form |
[ value ] |
representing a <CONST_EXPR> |
|
or a list of the form |
[ op, left, right ] |
representing a <FORMULA_EXPR> |
where |
op is '+' or '*' |
left, right are expr |
|
""" |
|
def exp_eval(expr): |
""" |
|
expr_eval(expr) <-- computes the value of expression tree expr |
|
>>> exp_eval( [ ] ) |
Traceback (most recent call last): |
... |
TypeError: exp_eval: invoked with invalid expression formula tree |
|
>>> exp_eval( [ 42 ] ) |
42 |
|
>>> exp_eval( [ '+', [2], [3] ] ) |
5 |
|
>>> exp_eval( [ '*', [ '+', [1], [2]], ['+', [3], [4]] ] ) |
21 |
|
It works on things that are not numbers but understand +, * |
|
>>> exp_eval( [ "hello" ] ) |
'hello' |
|
>>> exp_eval( [ '+', [ "hello" ], [ "world"] ] ) |
'helloworld' |
|
>>> exp_eval( [ '*', [ "h" ], [ 3 ] ] ) |
'hhh' |
|
Even on lists! |
|
>>> exp_eval( [ [ 42 ] ] ) |
[42] |
|
>>> exp_eval( [ '+', [ [1] ], [ [2, 3] ] ] ) |
[1, 2, 3] |
|
>>> exp_eval( [ '*', [ [1] ], [ 3 ] ] ) |
[1, 1, 1] |
|
Being Pythonic: |
If lists can be used to structure an expression, the tuples should |
also work. The singleton tuple (1,) is syntactically ugly |
|
>>> exp_eval( ( '*', ( '+', (1,), (2,)), ('+', (3,), (4,)) ) ) |
21 |
|
Or mixed tuples and lists: |
|
>>> exp_eval( ( '*', [ '+', (1,), (2,)], ('+', [3,], (4,)) ) ) |
21 |
|
Or even hashes if we put them together to satify [ ] index syntax: |
>>> exp_eval( { 0: '*', 1: [ '+', (1,), { 0: 2}], 2: ('+', [3,], (4,)) } ) |
21 |
|
|
But we need some more operations |
>>> exp_eval( [ '+', [2], ['-', [1], [2]] ] ) |
Traceback (most recent call last): |
... |
SyntaxError: exp_eval: unknown operation '-' |
|
""" |
|
val = None |
|
if len(expr) == 1: |
val = expr[0] |
|
elif len(expr) == 3: |
op = expr[0] |
lhs = expr[1] |
rhs = expr[2] |
if op == '+': |
val = exp_eval(lhs) + exp_eval(rhs) |
elif op == '*': |
val = exp_eval(lhs) * exp_eval(rhs) |
else: |
raise SyntaxError("exp_eval: unknown operation '" + op + "'") |
|
else: |
raise TypeError( |
"exp_eval: invoked with invalid expression formula tree") |
|
return val |
|
if __name__ == '__main__': |
import doctest |
doctest.testmod(verbose = 1) |
""" |
expression tree evaluator |
|
Evaluate an expression tree expr in the context of the symbols |
defined in the symtab dictionary. |
|
We define an expression with a grammar |
|
<EXPR> - an expression |
<OP> - an operator '+', '*' |
<NUMBER> - any valid python number |
|
<EXPR> := <CONST_EXPR> | <FORMULA_EXPR> |
<CONST_EXPR> := <NUMBER> |
|
<FORMULA_EXPR> := '(' <EXPR> <OP> <EXPR> ')' |
|
These expressions natually map onto trees |
|
Representing expressions as trees |
|
An expr tree can be a list of the form |
[ value ] |
representing a <CONST_EXPR> |
|
or a list of the form |
[ op, left, right ] |
representing a <FORMULA_EXPR> |
where |
op is '+' or '*' |
left, right are expr |
|
""" |
|
def exp_eval(expr): |
""" |
|
expr_eval(expr) <-- computes the value of expression tree expr |
|
>>> exp_eval( [ ] ) |
Traceback (most recent call last): |
... |
TypeError: exp_eval: invoked with invalid expression formula tree |
|
>>> exp_eval( [ 42 ] ) |
42 |
|
>>> exp_eval( [ '+', [2], [3] ] ) |
5 |
|
>>> exp_eval( [ '*', [ '+', [1], [2]], ['+', [3], [4]] ] ) |
21 |
|
It works on things that are not numbers but understand +, * |
|
>>> exp_eval( [ "hello" ] ) |
'hello' |
|
>>> exp_eval( [ '+', [ "hello" ], [ "world"] ] ) |
'helloworld' |
|
>>> exp_eval( [ '*', [ "h" ], [ 3 ] ] ) |
'hhh' |
|
Even on lists! |
|
>>> exp_eval( [ [ 42 ] ] ) |
[42] |
|
>>> exp_eval( [ '+', [ [1] ], [ [2, 3] ] ] ) |
[1, 2, 3] |
|
>>> exp_eval( [ '*', [ [1] ], [ 3 ] ] ) |
[1, 1, 1] |
|
Being Pythonic (not Pythonesque?) |
If lists can be used to structure an expression, the tuples should |
also work. The singleton tuple (1,) is syntactically ugly |
|
>>> exp_eval( ( '*', ( '+', (1,), (2,)), ('+', (3,), (4,)) ) ) |
21 |
|
But we need some more operations |
>>> exp_eval( [ '+', [2], ['-', [1], [2]] ] ) |
Traceback (most recent call last): |
... |
SyntaxError: exp_eval: unknown operation '-' |
|
""" |
|
val = None |
|
if len(expr) == 1: |
val = expr[0] |
|
elif len(expr) == 3: |
op = expr[0] |
lhs = expr[1] |
rhs = expr[2] |
if op == '+': |
val = exp_eval(lhs) + exp_eval(rhs) |
elif op == '*': |
val = exp_eval(lhs) * exp_eval(rhs) |
else: |
raise SyntaxError("exp_eval: unknown operation '" + op + "'") |
|
else: |
raise TypeError( |
"exp_eval: invoked with invalid expression formula tree") |
|
return val |
|
def exp_str_inorder(expr): |
""" |
exp_str_inorder(expr) <-- display expression tree in in-order traversal |
|
>>> exp_str_inorder(['*', [ '+', [1], [2]], [ '*', [2], [ '+', [40], [42]]]]) |
'((1+2)*(2*(40+42)))' |
|
""" |
|
val = "" |
|
if len(expr) == 1: |
val = str(expr[0]) |
|
elif len(expr) == 3: |
op = expr[0] |
lhs = expr[1] |
rhs = expr[2] |
val = "(" + exp_str_inorder(lhs) + op + exp_str_inorder(rhs) + ")" |
|
else: |
raise TypeError( |
"exp_str_inorder: invoked with invalid expression formula tree") |
|
return val |
|
def exp_str_postorder(expr): |
""" |
exp_str_postorder(expr) <-- display expression tree in post-order traversal |
|
>>> exp_str_postorder(['*', [ '+', [1], [2]], [ '*', [2], [ '+', [40], [42]]]]) |
'1 2 + 2 40 42 + * *' |
|
""" |
|
val = "" |
|
if len(expr) == 1: |
val = str(expr[0]) |
|
elif len(expr) == 3: |
op = expr[0] |
lhs = expr[1] |
rhs = expr[2] |
val = exp_str_postorder(lhs) + " " + exp_str_postorder(rhs) + " " + op |
|
else: |
raise TypeError( |
"exp_str_postorder: invoked with invalid expression formula tree") |
|
return val |
|
if __name__ == '__main__': |
import doctest |
doctest.testmod(verbose = 1) |