import GHC.Exts |
{- |
A ManyTree over type a, is a tree that consists of leaves with values |
of type a, and internal vertices which consist of lists of 0 or more |
ManyTree subtrees. |
|
Note: by having Internal nodes that have a list of subtrees, we can |
exploit map on that list to recurse down the tree. |
-} |
|
data ManyTree a = Leaf a | Internal [ ManyTree a ] |
deriving (Eq, Show) |
|
-- deconstructors, sometimes easier than using a pattern match |
getLeaf (Leaf x) = x |
getSubtrees (Internal subtrees) = subtrees |
|
-- example trees |
t1 :: ManyTree Int |
t1 = Internal [ Leaf 1, Leaf 2, Leaf 3] |
|
l2 :: [Int] |
l2 = (map getLeaf (getSubtrees t1)) |
t2 = Internal (map (\x -> Leaf (x *10)) l2) |
|
-- since trees are functional, you can have the same sub tree appearing |
-- in multiple places |
t3 = Internal [t1, t2] |
t4 = Internal [t1, t2, Leaf 42, Internal [t1, t2]] |
t5 = Internal [Leaf 42, Internal [Leaf 1, Leaf 2, Internal [] ] ] |
t6 = Internal [Internal [Internal [], Internal [] ], Internal [] ] |
|
-- do a depth first left to right traversal of tree t |
dfslr :: ManyTree a -> [a] |
dfslr (Leaf x) = [x] |
dfslr (Internal subtrees) = foldl (++) [] (map dfslr subtrees) |
|
{- Examples: |
*Main> dfslr t1 |
[1,2,3] |
*Main> dfslr t2 |
[10,20,30] |
*Main> dfslr t3 |
[1,2,3,10,20,30] |
-} |
|
-- transforms on trees |
|
-- apply a transform f to each leaf returning a tree of a possibly a |
-- different type |
mapLeaf :: (a->b) -> (ManyTree a) -> (ManyTree b) |
mapLeaf f (Leaf x) = Leaf (f x) |
mapLeaf f (Internal subtrees) = Internal ( map (mapLeaf f) subtrees ) |
|
{- Examples: |
*Main> mapLeaf (\x -> x * 10 ) t2 |
Internal [Leaf 100,Leaf 200,Leaf 300] |
|
*Main> mapLeaf (* 10 ) t2 |
Internal [Leaf 100,Leaf 200,Leaf 300] |
|
*Main> mapLeaf (\x -> (show x)++"x" ) t2 |
Internal [Leaf "10x",Leaf "20x",Leaf "30x"] |
*Main> mapLeaf (\x -> (show x)++"x" ) t4 |
Internal [Internal [Leaf "1x",Leaf "2x",Leaf "3x"], |
Internal [Leaf "10x",Leaf "20x",Leaf "30x"], |
Leaf "42x",Internal [Internal [Leaf "1x",Leaf "2x",Leaf "3x"], |
Internal [Leaf "10x",Leaf "20x",Leaf "30x"]]] |
-} |
|
-- apply a transform to each internal vertex, preserve the tree type |
mapInternal :: ([ManyTree a] -> [ManyTree a]) -> ManyTree a -> ManyTree a |
mapInternal f (Leaf x) = Leaf x |
mapInternal f (Internal subtrees) = |
Internal (f (map (mapInternal f) subtrees)) |
|
{- Examples: |
|
*Main> mapInternal (\st -> drop 1 st) t3 |
Internal [Internal [Leaf 20,Leaf 30]] |
|
*Main> mapInternal (drop 1) t3 |
Internal [Internal [Leaf 20,Leaf 30]] |
|
*Main> mapInternal (drop 1) t4 |
Internal [Internal [Leaf 20,Leaf 30],Leaf 42, |
Internal [Internal [Leaf 20,Leaf 30]]] |
-} |
|
-- YOUR ANSWERS SHOULD GO BELOW THIS LINE -- |
|
{- |
Name: |
StudentID: |
-} |
|
|
{- QUESTION 2.1 write the function numLeaves where |
numLeaves tree |
returns the number of Leaf elements in the tree. |
|
-} |
|
numLeaves :: ManyTree a -> Int |
numLeaves (Leaf _) = 1 |
numLeaves (Internal subtrees) = foldl (+) 0 (map numLeaves subtrees) |
|
-- an even terser solution, probably not better since it constructs a list |
-- numLeaves = length dfslr |
|
{- QUESTION 2.2 write the function fringeSize where |
fringeSize tree |
returns a tuple (nleaves, nempty) where |
nleaves - is the number of leaves in tree |
nempty - is the number of empty sub trees in tree, i.e. Internal [] |
|
-} |
|
|
fringeSize :: ManyTree a -> (Int, Int) |
fringeSize (Leaf _) = (1, 0) |
fringeSize (Internal []) = (0, 1) |
fringeSize (Internal subtrees) = foldl pairAdd (0,0) (map fringeSize subtrees) |
where |
-- define a pair add function instead of using this lambda in the fold |
-- (\(nl1, ne1) (nl2, ne2) -> (nl1+nl2, ne1+ne2)) |
pairAdd (x0, y0) (x1, y1) = (x0+x1, y0+y1) |
|
{- QUESTION 2.3 write the function cutEmptySubtrees where |
cutEmptySubtrees tree |
returns tree but with all subtrees consisting of only empty sub trees |
removed. |
|
Hint: use mapInternal, filter with a isNotEmpty predicate |
|
-} |
|
isEmpty (Internal []) = True |
isEmpty _ = False |
isNotEmpty tree = not $ isEmpty tree |
|
cutEmptySubtrees :: ManyTree a -> ManyTree a |
|
{- the "natural" implementation |
cutEmptySubtrees (Leaf x) = Leaf x |
cutEmptySubtrees (Internal subtrees) = |
Internal (filter isNotEmpty (map cutEmptySubtrees subtrees)) |
-} |
|
-- which leads to this purer version |
cutEmptySubtrees = mapInternal (filter isNotEmpty) |
|
{- QUESTION 2.4 what does this expression on tree return? |
mapInternal (sortWith numLeaves) tree |
-} |
|
{- ANSWER - it produces a new tree which is the original tree but the |
the subtrees of each Internal node of the tree are reordered |
by increasing numbers of leaves. |
|
-} |
|
{- Expanded discussion ... |
reorderByNumLeaves :: ManyTree a -> ManyTree a |
|
could have one implementation: |
reorderByNumLeaves (Leaf x) = (Leaf x) |
reorderByNumLeaves (Internal subtrees) = |
Internal ( sortWith numLeaves (map reorderByNumLeaves subtrees)) |
|
but when you inspect this you see that it is doing exctly what the mapInternal |
combinator is designed for, i.e. apply a transformation to each Internal node |
of the tree. Thus you get this: |
|
reorderByNumLeaves = mapInternal (sortWith numLeaves) |
|
-} |
|
-- TESTS - add you own additional ones |
showTest expr = putStr $ (show expr) ++ "\n" |
showNL = putStr "\n" |
|
runTests = do |
putStr "** Test Trees\n" |
showTest t1 |
showTest t2 |
showTest t3 |
showTest t4 |
showTest t5 |
showTest (t6 :: ManyTree Int) |
showNL |
|
putStr "** Test numLeaves and fringeSize\n" |
showTest (numLeaves t4) |
showTest (fringeSize t4) |
showTest (numLeaves t5) |
showTest (fringeSize t5) |
showNL |
|
putStr "** Test cutEmptySubtrees\n" |
showTest (cutEmptySubtrees t1) |
showTest (cutEmptySubtrees t2) |
showTest (cutEmptySubtrees t3) |
showNL |
showTest (cutEmptySubtrees t4) |
showTest (cutEmptySubtrees t5) |
showTest (cutEmptySubtrees t6 :: ManyTree Int) |
showNL |
|
putStr "** Test mapInternal expression\n" |
showTest (mapInternal (sortWith numLeaves) t5) |
{- |
A way of chaining a sequence of actions such that if one fails, |
all the the remaining ones fail. |
|
The state of a computation action is either OK s, in which case the |
resulting next state s is passed on, or the action fails and Failure |
is passed on. States are over some type a, thus State a |
|
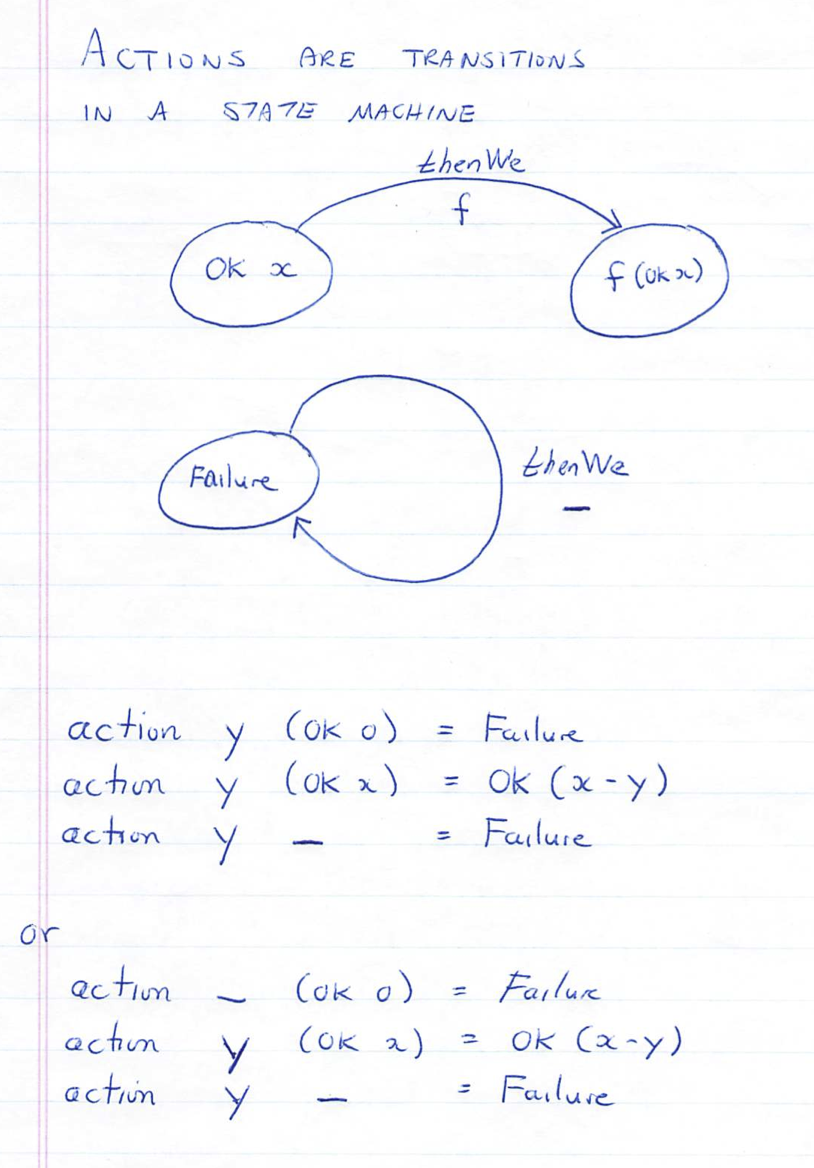
An action f is a function from state to state. The states can be |
of different types (see below). |
f :: State a -> State b |
|
Actions with compatible input and output states can be chained together |
using the thenWe function, normally in its infix form `thenWe` |
-} |
|
data State a = OK a | Failure |
deriving (Show, Eq) |
|
-- examples of actions that process an integer-like state |
myAction :: (Integral a, Eq a) => State a -> State a |
myAction (OK 0) = Failure |
myAction (OK x) = OK (x - 1) |
myAction _ = Failure |
|
myAction2 :: (Integral a, Eq a) => State a -> State (a, String) |
myAction2 (OK 0) = Failure |
myAction2 (OK x) = case x `mod` 2 of |
0 -> OK (x, "Even") |
1 -> OK (x, "Odd") |
myAction2 _ = Failure |
|
|
-- we chain actions together using thenWe, which has infix form `thenWe` |
|
thenWe :: State a -> (State a -> State b) -> State b |
thenWe (OK x) f = f (OK x) |
thenWe Failure _ = Failure |
|
{- Example: |
-- try testIt 3 and testIt 0 and testIt 1 |
-} |
|
testIt i = |
-- we need to start an action with an initial state |
OK i `thenWe` |
myAction `thenWe` |
myAction2 |
|
{- |
compose a function n >= 0 times with itself, where |
composeN n f |
is f . f . f . ... . f with f appearing n times. |
-} |
|
composeN :: Int -> (a -> a) -> (a -> a) |
composeN 0 f = id |
composeN n f = f . (composeN (n-1) f) |
|
|
actUntilFound :: (State a -> Bool) -> (State a -> State a) -> State a -> State a |
actUntilFound pred f curState = case curState of |
Failure -> Failure |
_ -> case pred curState of |
True -> curState |
False -> actUntilFound pred f (f curState) |
|
{- Example |
*Main> actUntilFound (\s -> (s == (OK 4) || s == (OK 0) )) myAction (OK 10) |
OK 4 |
*Main> actUntilFound (\s -> (s == (OK 4) || s == (OK 0) )) myAction (OK 3) |
OK 0 |
-} |
|
{- |
Given a predicate pred, action f , and initial state curState, perform |
the action over and over again until the predicate is False, then return |
the state just before the failure of the predicate, or Failure if any of |
the actions failed. |
|
Same idea as actUntilFound, but we want a state that we can resume on, so |
the second last state is more useful. |
-} |
|
actUntilFail :: (State a -> Bool) -> (State a -> State a) -> State a -> State a |
actUntilFail pred f curState = actUntilFail' pred f Failure curState |
|
{- Example |
*Main> actUntilFail (/= (OK 4)) myAction (OK 20) |
OK 5 |
*Main> actUntilFail (/= (OK 4)) myAction (OK 20) `thenWe` myAction |
OK 4 |
|
*Main> actUntilFail (/= (OK 4)) myAction (OK (2)) |
OK 0 |
*Main> actUntilFail (/= (OK 4)) myAction (OK (2)) `thenWe` myAction |
Failure |
-} |
|
-- recursor helper that has a previous state in addition to the current |
-- state so that the predicate can fail on the current state. |
|
actUntilFail' :: (State a -> Bool) -> (State a -> State a) -> |
State a -> State a -> State a |
|
actUntilFail' pred f prevState curState = case curState of |
Failure -> prevState |
_ -> case pred curState of |
-- move to next state and recurse |
True -> actUntilFail' pred f curState (f curState) |
-- we failed, return the previous successful state |
False -> prevState |
|
-- a version that has the helper defined inside, and thus does not need |
-- to propagate pred or f into the helper through paramaters |
|
actUntilFail2 pred f curState = actUntilFail2' Failure curState |
where |
actUntilFail2' prevState curState = case curState of |
Failure -> prevState |
_ -> case pred curState of |
-- move to next state and recurse |
True -> actUntilFail2' curState (f curState) |
-- we failed, return the previous successful state |
False -> prevState |
|
-- YOUR ANSWERS SHOULD GO BELOW THIS LINE -- |
|
{- |
Name: |
StudentID: |
-} |
|
{- QUESTION 1.1 extend the composeN function so that its value is id for n < 0 |
Call this new function composeN' |
-} |
composeN' :: Int -> (a -> a) -> (a -> a) |
composeN' n f = if n <= 0 |
then id |
else f . (composeN' (n-1) f) |
|
{- QUESTION 1.2 define the function actNTimes where |
actNTimes n f |
creates a new action consisting of performing action f |
n times in sequence. I.e chains n actions of f. |
|
NOTE: answer in the study questions! |
-} |
|
actNTimes :: Int -> (State a -> State a) -> (State a -> State a) |
actNTimes n f = composeN n (`thenWe` f) |
|
testIt' :: Integral a => a -> State (a, String) |
testIt' x = |
(OK x) `thenWe` |
(actNTimes 7 myAction) `thenWe` |
myAction2 |
|
{- QUESTION 1.3 define the function actUntilFailCount where |
actUntilFailCount pred f curState |
and given a predicate pred on states, an action f, and initial state |
curState, does exactly the same as actUntilFail, but also counts the |
number of actions performed, and returns a tuple |
(count, prevState) |
where count is the number of actions performed, and prevState is what |
actUntilFail would return. |
-} |
|
actUntilFailCount :: Num n => |
(State a -> Bool) -> (State a -> State a) -> State a -> (n, State a) |
|
actUntilFailCount pred f curState = actUntilFailCount' Failure 0 curState |
where |
actUntilFailCount' prevState count curState = case curState of |
-- failed, so stop |
Failure -> (count, prevState) |
|
-- is it safe to act? |
_ -> case pred curState of |
-- move to next state and continue |
True -> actUntilFailCount' curState (1+count) (f curState) |
-- we failed, return the previous successful state |
False -> (count, prevState) |
|
{- QUESTION 1.4 implment a variant of thenWe, called thenSeq, which remembers |
all the previous states that the actions generated. It is used like |
history `thenSeq` f |
where |
history is a stack of previous states (a list with most recent |
state at the beginning |
|
f is an action |
and the result depends on the history |
if the head of the history is Failure, then no further actions are taken |
otherwise the new state is added to the head of the lists of states |
|
See the tests below. |
|
-} |
-- solution 1, uses the @ operator to name the whole pattern |
thenSeq :: Eq(a) => [State a] -> (State a -> State a) -> [State a] |
-- no further actions, keep existing history |
thenSeq h@(Failure:history) f = h |
-- latest state is non-failure, so act and push onto history |
thenSeq h@(s:history) f = (s `thenWe` f) : h |
|
{- or |
-- solution 2 |
thenSeq :: Eq(a) => [State a] -> (State a -> State a) -> [State a] |
thenSeq (Failure:history) f = Failure : history |
thenSeq (s:history) f = (s `thenWe` f) : s : history |
|
or |
-- solution 3 |
thenSeq :: Eq(a) => [State a] -> (State a -> State a) -> [State a] |
thenSeq h case h of |
(Failure:history) = h |
(s:history) = (s `thenWe` f) : h |
|
-} |
|
|
-- testing thenSeq with the gcd algorithm, see tests below |
myAction3 :: Integral a => State (a,a) -> State (a, a) |
myAction3 ( OK (x, 0) ) = Failure |
myAction3 ( OK (x, 1) ) = OK (x, 1) |
myAction3 ( OK (x, y) ) = OK (y, x `mod` y) |
|
-- the initial state will be a list of the initial state |
myGcd ::Integral a => a -> a -> [ State (a, a) ] |
myGcd x y = [ OK (x, y) ] |
|
|
|
-- TESTS - add you own additional ones |
showTest expr = putStr $ (show expr) ++ "\n" |
showNL = putStr "\n" |
|
runTests = do |
putStr "** myAction `thenWe` myAction2\n" |
putStr "** testIt 3\n" |
showTest (testIt 3) |
putStr "** testIt 0\n" |
showTest (testIt 0) |
putStr "** testIt 1\n" |
showTest (testIt 1) |
showNL |
|
putStr "** actNTimes\n" |
showTest (testIt' 10) |
showTest (testIt' 9) |
showTest (testIt' 8) |
showTest (testIt' 7) |
showTest (testIt' 0) |
showNL |
|
putStr "** actUntilFound\n" |
showTest $ |
actUntilFound (\s -> (s == (OK 4) || s == (OK 0) )) myAction (OK 10) |
showTest $ |
actUntilFound (\s -> (s == (OK 4) || s == (OK 0) )) myAction (OK 3) |
showNL |
|
putStr "** actUntilFail\n" |
showTest $ actUntilFail (/= (OK 4)) myAction (OK 20) |
showTest $ actUntilFail (/= (OK 4)) myAction (OK 20) `thenWe` myAction |
showNL |
|
showTest $ actUntilFail (/= (OK 4)) myAction (OK (2)) |
showTest $ actUntilFail (/= (OK 4)) myAction (OK (2)) `thenWe` myAction |
showNL |
|
putStr "** actUntilFailCount\n" |
showTest $ actUntilFailCount (/= (OK 4)) myAction (OK 20) |
showNL |
|
showTest $ actUntilFailCount (/= (OK 4)) myAction (OK (2)) |
showNL |
|
putStr "** thenSeq\n" |
showTest $ [ (OK 10) ] `thenSeq` myAction `thenSeq` myAction |
-- 3 actions, but Failure occurs early |
showTest $ |
[ (OK 0) ] `thenSeq` myAction `thenSeq` myAction `thenSeq` myAction |
showTest $ composeN 5 (`thenSeq` myAction3) (myGcd 92 17) |
{- |
A way of chaining a sequence of actions such that if one fails, |
all the the remaining ones fail. |
|
The state of a computation action is either OK s, in which case the |
resulting next state s is passed on, or the action fails and Failure |
is passed on. States are over some type a, thus State a |
|
An action f is a function from state to state. The states can be |
of different types (see below). |
f :: State a -> State b |
|
Actions with compatible input and output states can be chained together |
using the thenWe function, normally in its infix form `thenWe` |
-} |
|
data State a = OK a | Failure |
deriving (Show, Eq) |
|
-- we chain actions together using thenWe, which has infix form `thenWe` |
|
thenWe :: State a -> (State a -> State b) -> State b |
thenWe (OK x) f = f (OK x) |
thenWe Failure _ = Failure |
|
-- TESTS - add you own additional ones |
showTest expr = putStr $ (show expr) ++ "\n" |
showNL = putStr "\n" |
|
-- now suppose our actions have parameters that affect the action |
|
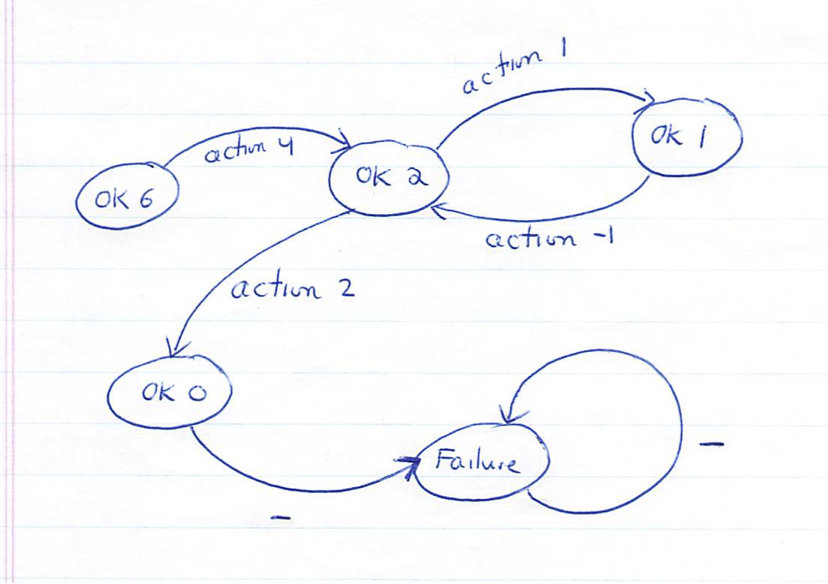
action :: (Num a, Eq a) => a -> State a -> State a |
action _ (OK 0) = Failure |
action y (OK x) = OK (x - y) |
action _ _ = Failure |
|
run1 = |
OK 10 `thenWe` (action 2) `thenWe` (action 4) |
|
run2 i = do |
OK i |
`thenWe` |
action 4 |
`thenWe` |
action 1 |
`thenWe` |
action (-1) |
`thenWe` |
action 2 |
`thenWe` |
action 1 |
|
|
-- what if we want to keep results from previous actions to inject into future |
-- actions? Then we need to pull the result, bind to a variable, then feed in later. |
-- while still chaining the actions. Let's do this in a number of stages. |
|
|
run3 i = |
-- we need to start an action with an initial state |
OK i `thenWe` |
|
-- but before we do the next action we want to save the value of i, so we need |
-- something that looks like an action, but also binds data to a variable. |
|
-- this is the identity action |
(\s_in -> |
-- grab the state but just pass it on, but it is exposed to us at this point. |
-- but not to the following actions. |
s_in ) |
|
`thenWe` |
action 3 |
|
|
run4 i = |
OK i `thenWe` |
-- we can move the chained actions inside, since chaining is associative |
-- and thus expose them to a previous state |
(\s_in -> |
-- grab the state and then pass it on to the future actions |
s_in |
`thenWe` |
action 3 |
) |
|
getState (OK x) = x |
run5 i = |
OK i `thenWe` |
(\s_in -> |
s_in |
`thenWe` |
-- now we can modify the actions |
action ((getState s_in)-1) |
) |
|
run6 i = |
OK i `thenWe` |
(\s_in -> |
-- grab the state and then pass it on to the future actions |
-- but instead of using getState to extract the state explicitly, we can |
-- introduce variable v, for later binding to the state |
(\v -> |
s_in |
`thenWe` |
action (v-1) |
) (getState s_in) -- the binding to v happens here |
) |
|
{- |
this passing on of current state, along with selective extraction of parts |
for future use is so common that it has been systematized in Haskell in a |
structure called a monad. |
-} |