Functional Programming
7. Mutable State



7.1 Capturing Mutable State In Closures

Having state around is very convenient, yet exposing it to arbitrary modification by other parts of a program is dangerous. Thus was invented object-oriented programming. In the functional world, state can be encapsulated in a closure, thus making it visible to the rest of the environment only though some kind of function interface.

The following example is yet another way to implement the counter object discussed previously.

code/State/Counters.rkt

    #lang racket
     
    ; using closures to capture and hide state
     
    ; (hide-state) returns a closure that when invoked increments the 
    ; previous stored value and then returns it.  The initial value is 0.
     
    (define hide-state
      (lambda  () 
        (let ( (internal 0) )  ; internal is not visible outside of hide-state
          (lambda () (set! internal (+ internal 1)) internal)
          )
        )
      )
     
    (display "hide-state")(newline)
    (define i (hide-state))
    (i)
    (i)
    (i)
     
    ; (make-counter init incr) returns a list of 3 closures.
    ; the first returns the current value of the counter
    ; the second adds incr and returns the current value
    ; the third subtracts incr and returns the current value
     
    (define make-counter
      (lambda (init incr)
        (let ( (counter init) )
          (list 
           (lambda () counter) ; return the current value
           (lambda () (set! counter (+ counter incr)) counter) ; increment and return the current value
           (lambda () (set! counter (- counter incr)) counter) ; decrement and return the current value
           ))))
     
    (newline)
    (display "make-counter")(newline)
    (define counter (make-counter 5 3))
    (define v (first counter))
    (define v+ (second counter))
    (define v- (third counter))
     
    (v)
    (v+)
    (v)
    (v+)
    (v-)
    (v)
    (v-)


7.2 Mutable Pairs and Non-list Structures

You should read Chapter 3 of Structure and Interpretation of Computer Programs. Follow this link http://mitpress.mit.edu/sicp/full-text/book/book.html for the full book, or warp directly to Chapter Three.

So far, every data structure we have created is acyclic. It is either a single atomic item, or a list. Lists can only give rise to tree-structured data. But you can construct your own data structures by using the basic building block of the dotted pair.
> (define P (cons 1 2))
> P
'(1 . 2)
> (displayln P)
(1 . 2)
> '(1 . 2)
'(1 . 2)

; cons creates a normal pair - note this is not a list!
; a list is a chain of pairs ending in the empty list
> (displayln (cons 1 '()))
(1)

> (displayln (cons 1 (cons 2 '())))
(1 2)

; you can build up your own data structures that are not lists

> (define Linear (cons 1 (cons 2 3)))
> Linear
'(1 2 . 3)

> (define Tree (cons (cons 1 2) (cons 3 4)))
; although the printing routine will try to print it as a list
> Tree
'((1 . 2) 3 . 4)


But if you want to implement a cyclic data structure, this will not work:
(define L (cons 42 L))
because L is not defined in the cons expression. Also, when you allow mutation of data structure, structrure sharing becomes more complicated.

Instead, you need to do much like one does procedurally, and create the data structure and then modify it to establish the circular link. To do this you need a mutable pair, one constructed by mcons. A mutable pair lets you modify the car and cdr of the pair later on.
; create a mutable pair - it is a list since the second element is a list
> (define C (mcons 42 '()))
> C
(mcons 42 '())

; now set the cdr of the list to point back to itself!
> (set-mcdr! C C)
> C
#0=(mcons 42 #0# )
; note how curly braces are used to indicate a mutable pair
> (displayln C)
#0= { 42 . #0# }

; thus getting an infinite list
; note, all the normal operations first, rest, car, cdr don't work on mutable lists
> (mcar (mcdr (mcdr (mcdr (mcdr (mcdr C))))))
42


Here is a direct translation of the queue data structure from that chapter. Note that Scheme r6rs introduced mutable pairs, and so this implementation uses the new operations: mcons, mcar, mcdr, set-mcar!, set-mcdr!.

code/State/queue.rkt

    #lang racket
     
    ; The queue motivated by chapter 3 of SICP
     
    ; a queue is a mutable pair, where the mcar is a pointer to the 
    ; front of the queue, and the mcdr is a pointer to the rear
    ; of the queue.  You insert at the rear (on the right) and remove
    ; from the front (on the left).
    ; The actual queue is a mutable-list formed by chaining mutable
    ; pairs.
     
    (define (q-front-ptr queue) (mcar queue))
    (define (q-rear-ptr queue)  (mcdr queue))
    (define (q-set-front-ptr! queue item) (set-mcar! queue item))
    (define (q-set-rear-ptr!  queue item) (set-mcdr! queue item))
    (define (q-empty? queue) (null? (q-front-ptr queue)))
    (define (q-make) (mcons '() '()) )
    (define (q-front queue)
      (if (q-empty? queue)
          (error "front-of-queue called with an empty queue" queue)
          (mcar (q-front-ptr queue))
          )
      )
     
    (define (q-insert! queue item)
      (let ( (new-pair (mcons item '() ) ) )
        (cond ( (q-empty? queue)
                (q-set-front-ptr! queue new-pair)
                (q-set-rear-ptr!  queue new-pair)
                queue)
              (else
               (set-mcdr! (q-rear-ptr queue) new-pair)
               (q-set-rear-ptr! queue new-pair)
               queue)
              )
        )
      )
     
    (define (q-remove! queue)
      (cond ( (q-empty? queue)
               (error "remove-queue! called with an empty queue" queue)
               )
              (else
               (let ( (front (mcar (q-front-ptr queue))) )
                (q-set-front-ptr! queue (mcdr (q-front-ptr queue)))
                front)
               )
              )
            )
     
    (define q (q-make))
    (q-insert! q 1)
    (q-front q)
    (q-insert! (q-insert! q 2) 3)
    (q-front q)
    (q-remove! q)
    (q-remove! q)
     
     
    ;(define (q-to-list q) )
    ;(define (q-from-list l) )


Here is a series of cell diagrams, where undef is the empty list.
The result of a create:



insert 1, then 2, then 3:



and two removes.



7.3 Promises and Delay/Force Revisited

We saw that key to lazy evaluation is to delay the evaluation of terms until they are needed. Scheme has delay/force primatives that do this.

To show that this is not magic, here is our own implementation. (pdelay expr) takes an expression and wraps it in a promise that delays its evaluation. (pforce p) takes the promise and evaluates it, thus fulfulling the promise. The fulfilled promise p will simply return the pre-computed value if it is forced again.

code/State/Promise.rkt

    #lang racket
     
    ; example of implementing your own delay/force
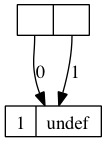
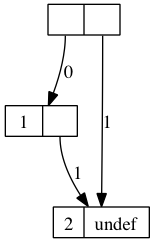
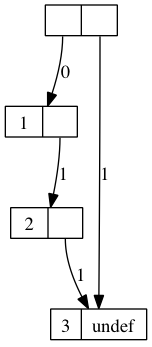
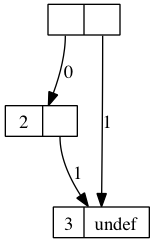
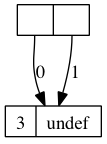
    ; a promise is a mutable pair
    ; if the first is 0, the second is a lambda () that when evaluated 
    ;   gives the value of the promise
    ; if the first is 1, the second is the actual value of the promise
    ;
    ; 
    (define (pdelay x) (mcons 0 (lambda () x)))
    (define (pforce promise) 
        (if (= 1 (mcar promise)) 
            ; already got value memoized
            (mcdr promise) 
            ; evaluate the promise and memoize it
            (begin (set-mcar! promise 1) 
                   (set-mcdr! promise ((mcdr promise))) 
                   (mcdr promise))
        )
    )
7. Mutable State
Notes on Functional Programming / Version 2.10 2014-02-24