Section 7: Inference Rules for Quantified Formulas and Equality
7.1: Bound Variable Renaming
We have already mentioned that the names of bound variables do not matter.
Everybody agrees that
for x being T holds P[x,y]
is equivalent to
for z being T holds P[z,y]
Sometimes we would like to rename some of the identifiers in a formula
in order to make it easier to read.
How do we ensure that our renaming does not change the meaning
of the original formula?
Given a formula 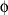 , we may change the name of a bound variable in
, we may change the name of a bound variable in 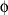 and
obtain a formula
and
obtain a formula 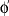 equivalent to
equivalent to 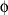 provided
no occurrence of an object identifier that was free in
provided
no occurrence of an object identifier that was free in 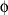 becomes bound in
becomes bound in 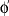 , and every occurrence of a bound object
identifier in
, and every occurrence of a bound object
identifier in 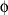 has the same binding in
has the same binding in 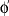 .
(Note, it is not enough that bound object identifiers remain bound, they
must remain bound to the same quantifier.)
.
(Note, it is not enough that bound object identifiers remain bound, they
must remain bound to the same quantifier.)
Whenever we rename bound variables we refer to the rule of inference
called Bound Variable Renaming.
Bound variable renaming does not require any justification in MIZAR texts.
Let us look at some examples.
-
for z being T holds P[z,y]
is equivalent to
for aaaa being T holds P[aaaa,y]
and is not equivalent to
for y being T holds P[y,y]
as a formerly free object identifier ( the y in P[z,y] )
has become bound.
-
ex z being T st for x being T holds P[x,y,z]
is not equivalent to
ex z being T st for z being T holds P[z,y,z]
as a free object identifier x in for x being T holds P[x,y,z]
has become bound in for z being T holds P[z,y,z].
-
ex z being T st for x being T holds P[x,y,z]
is not equivalent to
ex y being T st for x being T holds P[x,y,y]
as a free object identifier y has become bound.
7.2: Proper Free Substitution
Inference rules for quantifiers involve renaming of object identifiers
and a textual operation on formulas, called proper free substitution.
This is its definition:
We say the formula 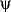 comes from formula
comes from formula 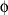 by
proper free substitution of object identifier
by
proper free substitution of object identifier  for
object identifier
for
object identifier  if
if
-
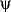 is exactly like
is exactly like 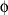 except that
wherever
except that
wherever 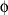 has free occurrences of
has free occurrences of  ,
,
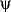 has free occurrences of
has free occurrences of  , and
, and
-
the sort of
 is the same as the sort of
is the same as the sort of  .
.
It is important to remember that proper free substitution is not an
inference rule.
It is a rule for editing formulas textually.
For example, the formula
Knave[Fred] & Knight[Wilma] implies (ex Fred being PERSON st Tells[Fred,s])
becomes, under proper free substitution of Wilma for
Fred, the formula
Knave[Wilma] & Knight[Wilma] implies (ex Fred being PERSON st Tells[Fred,s])
This in turn becomes, under proper free substitution of
Hello for s, the formula
Knave[Wilma] & Knight[Wilma] implies (ex Fred being PERSON st Tells[Fred,Hello])
We use the notation 
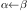 to stand for the formula resulting
from the proper free substitution of
to stand for the formula resulting
from the proper free substitution of  for
for  in formula
in formula  .
Another way to think of this notation is of replacing every
free occurrence of
.
Another way to think of this notation is of replacing every
free occurrence of  by
by  without introducing any
new bound occurrences of
without introducing any
new bound occurrences of  .
Note that there is no notation for proper free substitution that is
consistently used by all authors of logic texts,
so it is always important to determine the convention used for
each particular work.
.
Note that there is no notation for proper free substitution that is
consistently used by all authors of logic texts,
so it is always important to determine the convention used for
each particular work.
This notation lets us define three more inference rules.
7.3: Equality Elimination, =E
Equality elimination is the rule that we apply when making a reference to
a known equality between two objects.
 = =  , , 
 | provided  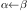 is identical to is identical to  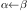
|
This requires some explanation. The intended meaning of this rule is that
we can exchange some or all free occurrences of  and
and  in a formula
provided
in a formula
provided  =
= .
The condition attached to the formula says just that.
It might be easier to understand the formula if you look at it this way.
Knowing that
.
The condition attached to the formula says just that.
It might be easier to understand the formula if you look at it this way.
Knowing that  =
= we may think that
we may think that  is just another name
of the same object named by
is just another name
of the same object named by  . So, let us choose
. So, let us choose  as the only name
that we use,
as the only name
that we use,  is just an alias.
is just an alias.
Examples.
- Equality is symmetric.
environ
given a, b being THING;
1: a = b;
begin
b = a by 1; == =E
This example may look cryptic. The two premises needed by the inference rule
are formed by the same formula a=b. And indeed,
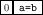
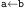 is identical to
is identical to
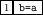
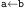 as both of them are b=b.
as both of them are b=b.
- Equality is transitive.
environ
given a, b, c being THING;
1: a = b;
2: b = c;
begin
a = c by 1, 2; == =E
Here we see that
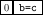
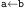 is identical to
is identical to
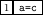
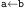 .
.
-
environ
given a, b being THING;
1: P[a];
2: not P[b];
begin
R: now
assume step1: a = b;
step2: not P[a] by step1, 2; == =E
thus step3: contradiction by 1, step2; == ContrI
end;
a <> b by R; == PbyC
- MIZAR automatically processes equality as a reflexive, symmetric
and transitive relation. (Reflexivity is expressed by the Equality Introduction (=I) rule introduced earlier.)
Therefore, the following argument requires only one step of inference.
environ
given a, b, c being THING;
1: P[a];
2: not P[c];
3: a = b;
begin
b <> c by 1, 2, 3; == No single inference rule suffices.
== Mizar can figure out which basic rules are involved.
It is a worthwhile exercise to write the above using only single inference
rules.
7.4: Universal Elimination, UE
Universal elimination is used to convert a general
statement about any object into a specific statement about a
particular object.
for  being
being  holds
holds 

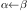
where  is any visible object identifier of sort
is any visible object identifier of sort  .
.
This rule is sometimes called universal instantiation, or universal
specialization, because it specializes a general statement
about any object into
a specific statement about a particular object.
It represents our intuition that what holds for everything must
hold for any specific thing.
Look at these inferences.
environ
given Fred being PERSON;
given Hello being STATEMENT;
KnightSpeak: for y being PERSON holds
for s being STATEMENT holds
Knight[y] & Tells[y,s] implies True[s];
begin
== Specialize the y to Fred.
1: for s being STATEMENT holds
Knight[Fred] & Tells[Fred,s] implies True[s]
by KnightSpeak; == UE
== Further Specialize the s in 1 to Hello.
2: Knight[Fred] & Tells[Fred,Hello] implies True[Hello] by 1; == UE
== You must instantiate in the order that the quantifiers occur
== thus attempting to specify s to Hello will not work.
3: for y being PERSON holds
Knight[y] & Tells[y,Hello] implies True[Hello] by KnightSpeak;
== That is, when you have a list of universal quantifiers, only the
== leading ones can be eliminated.
== In order to achieve the inner universal quantifier elimination you
== have to use Universal Introduction, see below.
7.5: Existential Introduction, ExI
This next rule corresponds to our intuition that if a formula holds
for a particular thing, then we can discard some information
and simply say that the formula holds for some thing.
Using this rule we obtain a weaker formula than the premise
and in the process we lose information.
Suppose that you have the formula A[x] & B[x] in some context,
where x is of sort THING.
This means that there is a precise object, named x, which satisfies
the formula.
We can then certainly write:
ex y being THING st A[y] & B[y]
This formula is read as ``There exists some object y satisfying
A[y] & B[y]''.
We know that this is true at least in the case that y denotes
the same object as x.
There may also be objects other than the one denoted by x
which also satisfy the formula.
But we also know that the following formula is true for exactly the
same reasons:
ex y being THING st A[y] & B[x]
Note how only the argument to predicate A was changed.
In general we can do the following kind of inference.

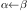
ex  being
being  st
st 
where  is a visible object identifier of sort
is a visible object identifier of sort  .
.
This rule is sometimes called Existential Generalization.
Note the particular form of this rule.
For example, here are different existential statements
that can be concluded from the same formula.
environ
given x,y being THING;
A: P[x,y,x];
begin
== Generalize with respect to y.
ex a being THING st P[x,a,x] by A; == ExI
== Generalize with respect to x.
ex b being THING st P[b,y,b] by A; == ExI
== Generalize with respect to the first x.
ex c being THING st P[c,y,x] by A; == ExI
== Generalize with respect to nothing.
ex d being THING st P[x,y,x] by A; == ExI
Here is an example of using universal elimination and
existential introduction in an argument.
environ
given Fred being PERSON;
given Hello being STATEMENT;
A1: for x being PERSON holds
ex s being STATEMENT st
(Tells[x,s] & Tells[x,Hello] & s <> Hello & True[s]);
begin
== Here we universally instantiate, substituting Fred for x
== and eliminating the universal quantifier.
1: ex s being STATEMENT st
(Tells[Fred,s] & Tells[Fred,Hello] & s <> Hello & True[s]) by A1; == UE
== Existential generalization, replace all occurrences
== of Hello by t, and add the existential quantifier
2: ex t being STATEMENT st
ex s being STATEMENT st
(Tells[Fred,s] & Tells[Fred,t] & s <> t & True[s]) by 1; == ExI
== Existentially generalize, replace only the first
== of Fred occurrences by y, and add the existential quantifier.
3: ex y being PERSON st
ex t being STATEMENT st
ex s being STATEMENT st
(Tells[y,s] & Tells[Fred,t] & s <> t & True[s]) by 2; == ExI
7.6: Examples of Universal Elimination, and Existential Introduction
environ
given Fred being PERSON;
given Hello being STATEMENT;
KnightSpeak: for y being PERSON for s being STATEMENT
holds Knight[y] & Tells[y,s] implies True[s];
A1: Knight[Fred];
A2: Tells[Fred, Hello];
begin
== Here is an example of Universal Instantiation.
1: for s being STATEMENT holds
Knight[Fred] & Tells[Fred,s] implies True[s] by KnightSpeak;
== And here is an example of Existential Generalization.
1a: ex s being STATEMENT st Tells[Fred,s] by A2;
1b: ex x being PERSON, s being STATEMENT st Tells[x,s] by A2;
1c: ex x being PERSON st Tells[x,Hello] by A2;
== This is also correct.
1d: ex x being KNIGHT, s being STATEMENT st Tells[Fred,Hello] by A2;
KnightSpeak1: for t being STATEMENT for x being PERSON
holds Knight[x] & Tells[x,t] implies True[t] proof
let t be STATEMENT;
== now we have to show the "for x ..." part
let x be PERSON;
thus Knight[x] & Tells[x,t] implies True[t] by KnightSpeak;
end;
2: for y being PERSON holds
Knight[y] & Tells[y,Hello] implies True[Hello] by KnightSpeak1;
2a: for y being PERSON holds
Knight[y] & Tells[y,Hello] implies True[Hello] proof
let y be PERSON;
1: for s being STATEMENT holds
Knight[y] & Tells[y,s] implies True[s] by KnightSpeak;
thus
Knight[y] & Tells[y,Hello] implies True[Hello] by 1;
end;
3: Knight[Fred] & Tells[Fred,Hello] implies True[Hello] by KnightSpeak;
4: True[Hello] by A1, A2, 3;
7.7: Universal Introduction, UI
To introduce a universal quantifier we do another kind of hypothetical
reasoning, called universal generalization or universal
introduction.
The intuition here is that to prove that some formula holds for all objects
we show that it holds for any arbitrarily selected but fixed object.
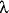 : now : now
| |
|
|
let  be be  ; ;
|
|
|
.
|
|
|
.
|
|
|
.
|
|
|
thus  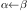 Justification Justification
|
|
end;
|
|
for  being
being  holds
holds  by
by 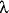
where  and
and  are permitted to be identical object identifiers.
The formula
are permitted to be identical object identifiers.
The formula 
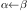 must not contain any
free occurrences of any object identifier introduced inside the now
other than
must not contain any
free occurrences of any object identifier introduced inside the now
other than  .
.
Remember that any formula visible at line 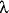 which has
which has
 free will not be properly
visible inside the reasoning. The `value' of the object identifier
free will not be properly
visible inside the reasoning. The `value' of the object identifier  defined outside of the reasoning
is not arbitrary (many things could have already been stated about it),
and so any formula with a free
defined outside of the reasoning
is not arbitrary (many things could have already been stated about it),
and so any formula with a free  from outside the proof
is actually referring to a different object than the
from outside the proof
is actually referring to a different object than the  inside the proof.
(Go back now and reread the definition of visibility).
inside the proof.
(Go back now and reread the definition of visibility).
So for example, the following inference is correct
environ
given Fred being PERSON;
A: Knight[Fred];
begin
== We prove that for all persons, Fred is a knight.
== (Do not worry that it does not make much sense.)
1: now
let p be PERSON;
thus Knight[Fred] by A; == RE
end;
for p being PERSON holds Knight[Fred] by 1 == UI
while this one is not:
environ
given Fred being PERSON;
A: Knight[Fred];
begin
== This says the same as in the previous example.
== But it tries to prove that all persons are knights!
1: now
let Fred be PERSON; == You can do it.
== The following does not work as Fred mentioned in axiom A
== is not the same Fred as inside this reasoning.
thus Knight[Fred] by A;
****************************99
**
** 99 Your inference is not accepted by the checker.
**
end;
for p being PERSON holds Knight[Fred] by 1; == UI
********************************************99
**
** 99 Your inference is not accepted by the checker.
**
== Note. The reasoning at 1 was incorrect, still we can make
== a reference to it.
== The above does not work, but the step below does.
for Fred being PERSON holds Knight[Fred] by 1; == UI
We can now complete the example where we wanted to instantiate
an inner quantifier.
Note how we do renaming of the quantified object from y in the now,
to yy in the concluded formula 2.
environ
given Fred being PERSON;
given Hello being STATEMENT;
KnightSpeak: for y being PERSON holds
for s being STATEMENT holds
Knight[y] & Tells[y,s] implies True[s];
begin
== We want to substitute Hello for s.
1: now
let y be PERSON;
1: for s being STATEMENT holds
Knight[y] & Tells[y,s] implies True[s] by KnightSpeak; == UE
thus Knight[y] & Tells[y,Hello] implies True[Hello] by 1; == UE
end;
2: for yy being PERSON holds
Knight[yy] & Tells[yy,Hello] implies True[Hello] by 1 == UI
7.8: Existential Elimination, ExE
Our last inference rule is used to convert an existential statement about
some object, into a statement about a specific object.
The idea is that if we have
ex  being
being  st
st 
then 
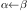 will hold for some specific object
will hold for some specific object  of sort
of sort  .
But since we do not know what that object actually is, the name
.
But since we do not know what that object actually is, the name
 that we give it should be different from any other visible name.
Otherwise, unexpectedly, we can give a new meaning to a name
that we have been using.
The inference rule looks like
that we give it should be different from any other visible name.
Otherwise, unexpectedly, we can give a new meaning to a name
that we have been using.
The inference rule looks like
ex  being
being  st
st 
consider  being
being  such that
such that 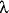 :
: 
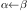
Where the formula  must not contain any free
must not contain any free  .
.
The consider statement introduces a new object with identifier  and sort
and sort  .
This will hide all prior instances of
.
This will hide all prior instances of  and any prior
formulas with a free
and any prior
formulas with a free  cannot be used in the current scope as they
contain the now hidden previous
cannot be used in the current scope as they
contain the now hidden previous  .
.
Here is a complicated example illustrating this inference rule.
environ
given Hello being STATEMENT;
given Fred being PERSON;
== Hello is a true statement.
Fact1: True[Hello];
== Fred always lies.
Fact2: for s being STATEMENT holds Tells[Fred,s] implies not True[s];
== Every person is either a Knight or a Knave, but not both.
Opp: for a being PERSON holds Knight[a] iff not Knave[a];
== A person is a knight if and only if every statement
== they say is true.
Veracity: for a being PERSON holds
Knight[a] iff
(for s being STATEMENT holds Tells[a,s] implies True[s]);
== If at least one of the things you say is false
== then everything you say is false.
Consistency: for a being PERSON holds
(ex s being STATEMENT st Tells[a,s] & not True[s]) implies
(for s being STATEMENT holds Tells[a,s] implies not True[s]);
== Every person says at least one thing.
Verbosity: for p being PERSON holds ex s being STATEMENT st Tells[p,s];
== Some person says everything.
BlabberMouth: ex p being PERSON st for s being STATEMENT holds Tells[p,s];
begin
== We demonstrate that there is some person who says Hello.
== Use the fact that blabber mouth exists.
consider blabber being PERSON such that
1: for s being STATEMENT holds Tells[blabber,s]
by BlabberMouth; == ExE
== Combine this with the fact that Hello is a statement.
2: Tells[blabber, Hello] by 1; == UE
== Now existentially generalize
ex p being PERSON st Tells[p,Hello] by 2; == ExI
== We prove that there exists some person p such that if they
== are a knight then all statements are true.
== This example should demonstrate to you that the scope of
== an existential quantifier better not be a conditional,
== if it is possible for the antecedent to be false for some
== object.
consider blabber being PERSON such that
1: for s being STATEMENT holds Tells[blabber,s]
by BlabberMouth; == ExE
2': now
assume A: Knight[blabber];
3: for s being STATEMENT holds
Tells[blabber,s] implies True[s]
by Veracity, A; == UE, EqE
4: now
let s be STATEMENT;
5: Tells[blabber,s] by 1; == UE
thus True[s] by 3, 5; == UE, IE
end;
thus for s being STATEMENT holds True[s] by 4; == UI
end;
2: Knight[blabber] implies
(for s being STATEMENT holds True[s]) by 2'; == II
ex p being PERSON st
(Knight[p] implies (for s being STATEMENT holds True[s]))
by 2; == ExI
== Note that we can reference 2' directly.
ex p being PERSON st
(Knight[p] implies (for s being STATEMENT holds True[s]))
by 2'; == ExI
In the example above we have indicated the lines where two basic rules
of inference have been used, in the indicated order.
Although, we need not doing it to satisfy the MIZAR checker, sometimes
it helps to clarify things for ourselves.
7.9: De Morgan's Laws for Quantifiers
As with derived inference rules for propositional calculus, there are
derived inference rules for quantifiers.
Here we mention only the so called De Morgan's Laws (See 6.3.11 for the De Morgan's laws in their quantifier-free version.)
and attach the corresponding argument using only the basic rules of inference.
-
not (for  being
being  holds
holds  )
)
ex  being
being  st not
st not 
environ
A1: not (for a being T holds PHI[a]);
begin
1: now
assume
step1: not (ex a being T st not PHI[a]);
step2: now
let x be T;
step3': now assume
step3: not PHI[x];
step4: ex a being T st not PHI[a] by step3; == ExI
thus contradiction by step1, step4; == ContrI
end;
thus PHI[x] by step3'; == PbyC
end; == We have just shown: for a being T holds PHI[a].
thus contradiction by A1, step2; == ContrI
end;
ex a being T st not PHI[a] by 1 == PbyC
-
not (ex  being
being  st
st  )
)
for  being
being  holds not
holds not 
environ
A1: not (ex a being T st PHI[a]);
begin
1: now
let x be T;
step0: now
assume step1: PHI[x];
step2: ex a being T st PHI[a] by step1; == ExI
thus contradiction by A1, step2; == ContrI
end;
thus not PHI[x] by step0 == NI
end;
for a being T holds not PHI[a] by 1; == UI
-
for  being
being  holds not
holds not 
not (ex  being
being  st
st  )
)
environ
A1: for a being T holds not PHI[a];
begin
1: now
assume step1: ex a being T st PHI[a];
consider x being T such that
step2: PHI[x] by step1; == ExE
step3: not PHI[x] by A1; == UE
thus contradiction by step2, step3; == ContrI
end;
not (ex a being T st PHI[a]) by 1 == PbyC
-
ex  being
being  st not
st not 
not (for  being
being  holds
holds  )
)
environ
A1: ex a being T st not PHI[a];
begin
1: now
assume step1: for a being T holds PHI[a];
consider x being T such that
step2: not PHI[x] by A1; == ExE
step3: PHI[x] by step1; == UE
thus contradiction by step2, step3; == ContrI
end;
not (for a being T holds PHI[a]) by 1 == PbyC
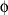 , we may change the name of a bound variable in
, we may change the name of a bound variable in 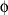 and
obtain a formula
and
obtain a formula 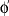 equivalent to
equivalent to 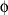 provided
no occurrence of an object identifier that was free in
provided
no occurrence of an object identifier that was free in 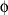 becomes bound in
becomes bound in 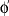 , and every occurrence of a bound object
identifier in
, and every occurrence of a bound object
identifier in 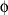 has the same binding in
has the same binding in 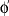 .
(Note, it is not enough that bound object identifiers remain bound, they
must remain bound to the same quantifier.)
.
(Note, it is not enough that bound object identifiers remain bound, they
must remain bound to the same quantifier.)
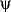 comes from formula
comes from formula  for
object identifier
for
object identifier  if
if

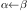 to stand for the formula resulting
from the proper free substitution of
to stand for the formula resulting
from the proper free substitution of 

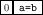
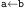 is identical to
is identical to
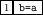
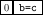
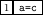
 holds
holds 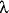 : now
: now