implies 
Hypothetical reasoning is a special form of proof in which we start by assuming the truth of a formula. The formula that we assume need not actually be true, thus the reasoning is termed hypothetical.
To justify a conditional of the form
implies we must be able show that can be derived from
(and possibly using also other formulae that are available for reference).
The demonstration of this fact takes the form of a reasoning that
starts with now.
The basic form of this rule is:
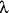 : | now |
|
assume A: ;
| |
| . | |
| . | |
| . | |
|
thus Justification
| |
| end | |
implies by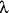
where, Justification is either simple, using by, or forms a proof (see below). The entire reasoning may have a label in front of now which is referenced when we apply the II rule. This rule is named Implication Introduction, as it lets us introduce a formula with implies as the main connective. Consider the following example:
environ
given x being PERSON;
Ax1: P[x] implies Q[x];
Ax2: Q[x] implies R[x];
begin
1: now
assume A: P[x];
a1: Q[x] by A, Ax1; == Rule: IE
thus R[x] by a1, Ax2; == Rule: IE
end;
P[x] implies R[x] by 1; == Rule: II
2: now
assume A: (P[x] implies Q[x]) & (Q[x] implies R[x]) & P[x];
a1: P[x] by A; == CE
a2: P[x] implies Q[x] by A; == CE
a3: Q[x] by a1, a2; == IE
a4: Q[x] implies R[x] by A; == CE
thus R[x] by a3, a4; == IE
end;
( (P[x] implies Q[x]) & (Q[x] implies R[x]) & P[x] ) implies R[x]
by 2; == II
Remember that we stated that only statements that are true in their contexts can appear in an argument. But what happens when both a statement and its negation are true in the same context? This is a contradiction, and indicates an internal inconsistency in the current context. We have a special formula, contradiction, that can be derived using the following inference rule:
, not The always false, constant formula contradiction and the ContrI rule of inference are introduced for convenience, we could work without them. Example:
. . .
14: Knight[John] . . .
. . .
25: not Knight[John] . . .
. . .
contradiction by 14, 25; == ContrI
. . .
It should be impossible to establish contradiction (in any consistent proof system) by correct reasoning from consistent premises. If you do, you are permitted to conclude that the assumptions you made which led to contradiction must be false.
This form of argument was illustrated by our knights and knaves example.
In this kind of argument we typically begin by assuming that
some statement is true, and then proceed to reason
on the basis of this assumption.
If we encounter some kind of contradiction or absurd situation we stop
reasoning and conclude that, since leads to nonsense, cannot be
true and so not must be true.
This kind of reasoning is called proof by contradiction and forms
the essence of the Negation Introduction rule.
|
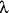: | now |
|
assume A: ;
| |
| . | |
| . | |
| . | |
| thus contradiction Justification | |
| end |
by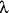
Now you see why this form of proof is named Negation Introduction; it provides us with the means to obtain a negated formula (if possible). For example:
environ
given glass being CONTAINER;
given juice being DRINK;
A1: Full[glass] implies Fresh[juice];
A2: not Fresh[juice];
begin == We show that: not Full[glass]
S: now
assume A: Full[glass];
1: Fresh[juice] by A, A1; == IE
thus contradiction by 1,A2; == ContrI
end;
not Full[glass] by S; == NI
The next example illustrates how to employ a proof by contradiction when proving a formula that does not have not as its main connective.
environ
given glass being CONTAINER;
begin == We will demonstrate that the following weird formula is always true:
== (not Full[glass] implies Full[glass]) implies Full[glass]
1: now
assume a: not Full[glass] implies Full[glass];
S: now == We prepare for Negation Introduction
assume b: not Full[glass];
c: Full[glass] by a, b; == MP
thus contradiction by c, b; == ContrI
end;
d: not not Full[glass] by S; == NI
thus Full[glass] by d == NE
end;
(not Full[glass] implies Full[glass]) implies Full[glass] by 1; == II
In the inner now we have showed that not Full[glass] leads to contradiction. From the reasoning we obtained not not Full[glass] using the NI rule. Then we stripped off the double negation using the NE rule. To simplify matters, we introduce an alternative form of proof by contradiction. This alternative form of the NI rule will be named proof by contradiction with the abbreviation PbyC.
|
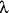: | now |
|
assume Contra: not ;
| |
| . | |
| . | |
| . | |
| thus contradiction Justification | |
| end |
by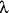
Do you see that this rule is superfluous? The same effect always can be
achieved by proving not not using NI and then
stripping off the double negation by NE.
We will conclude this section with an excursion into a non-existing world. It is the world where contradiction has been assumed as one of the axioms. This would make contradiction true. But since contradiction is false, it cannot be so; such a world does not exist, and we can expect a lot of surprising results. (Note that despite the fact that the world does not exist---false assumptions---we can talk about it. This should not be surprising at all, the politicians do it all the time, and we do it only in this place.)
We will prove that in such a world every formula can be proven.
environ
StrangeWorld: contradiction;
begin
1: now
assume not ArbitraryFormula[];
thus contradiction by StrangeWorld == RE
end;
ArbitraryFormula[] by 1; == PbyC
So, if you manage to get a contradiction in any reasoning then you can prove whatever you wish. This is the reason we try to avoid contradictory worlds at all cost. In using the NI rule, the obtained contradiction is usually blamed on the locally made assumption.
The basic rules of inference discussed in section 5.2 and the hypothetical reasoning rules (II and NI) are sufficient for conducting arguments. However, using only this small set of rules makes arguments quite lengthy. Therefore, we introduce the notion of a derived rule of inference which we will use instead of the lengthy sequence of basic rules. Look at an example.
environ
given x, cow being THING;
1: Wood[x] implies CanCook[x, cow];
2: CanCook[x, cow] implies Eat[cow];
3: Wood[x];
begin
step1: CanCook[x, cow] by 1, 3; == IE
step2: Eat[cow] by 2, step1; == IE
In any similar situation and using only the basic rules we will have to repeat the two steps of the Modus Ponens application. However, we will say that by virtue of the above example we are free to use the following derived rule of inference:
implies , implies 
,
One can certainly think about a number of similar rules, one for each number of repeated Modus Ponens. Now, do we have to remember all these derived rules? The answer is no. The MIZAR processor does not require us to specify any rule of inference in our arguments. It is the processor that checks whether any step we made in our reasoning can be obtained by a sequence of applications of basic inference steps.
Below, we list a number of the more popular derived inference rules. We will require you to annotate some of your derivations. Understanding the rules of inference is crucial to learning proof methods.
implies , not
The above rule corresponds to the following argument in which we use only basic inference rules.
environ
given 172 being COURSE;
1: Goodmarks[172] implies Pass[172];
2: not Pass[172];
begin
1: now
assume step1: Goodmarks[172];
step2: Pass[172] by step1, 1; == IE
thus step3: contradiction by 2, step2; == ContrI
end;
not Goodmarks[172] by 1; == PbyC
or not
The above rule corresponds to the following argument in which we use only basic rules of inference:
environ
given s being STATEMENT;
== No other premises.
begin
1: now
assume step1: not (True[s] or not True[s]);
step2: now
assume step3: not True[s];
step4: True[s] or not True[s] by step3; == DI
thus step5: contradiction by step1, step4; == ContrI
end;
step6: True[s] by step2; == PbyC
step7: True[s] or not True[s] by step6; == DI
thus contradiction by step1, step7 == ContrI
end;
True[s] or not True[s] by 1 == PbyC
implies , implies implies
The same effect as from applying the Chained Implication rule can be obtained using only basic rules:
environ
given x, cow being THING;
1: Wood[x] implies CanCook[x, cow];
2: CanCook[x, cow] implies Eat[cow];
begin
1: now
assume step1: Wood[x];
step2: CanCook[x, cow] by 1, step1; == MP
thus step3: Eat[cow] by 2, step2; == MP
end;
Wood[x] implies Eat[cow] by 1 == II
You are strongly encouraged to demonstrate that the following derived rules of inference correspond to a sequence of basic inferences. (We do not introduce standard acronyms for the names of derived rules.)
implies implies not implies not implies
implies , implies or implies or , implies , implies
iff implies , implies iff & ) or (not & not ) & ) or (not & not ) iff
iff , not
& or not ) or & not ) & ) or not or ) & not
or , or not , implies or or implies implies implies The construction DistributedStatement with syntax
provides us with an alternative way of recording formulas together with their justification. Distributed---because pieces of a formula are distributed along the reasoning. We will discuss the details of this distribution in section 8.4. Here, we would like to point out that distributed formulas can be referenced in a way similar to the regular ones. Consider a reasoning:
. . .
1': now
. . .
. . .
. . .
end;
We can always write a compact sentence
. . .
1'': . . . by 1';
. . .
which will be accepted as correct and in the text that follows, it does not matter whether we make a reference to 1'' or to 1'---both these labels refer to the same formula. For reference, a formula need not be recorded in a compact way; the distributed version of the formula suffices.
We can say that the II rule provides us with the distributed means of recording a conditional: the connective implies need not be mentioned at all. Analogous remarks apply for the NI rule.
A MIZAR text usually contains many statements and reasonings. At every step in a reasoning it is important to know what formulas and objects can or cannot be used to establish the next step. To this end we introduce the notion of visibility of identifiers, for both object identifiers and formula labels.
Recall that a MIZAR Article consists of two parts: the Environment and the TextProper. The environment contains two main kinds of statements: axioms, which are formulas with a label, and global constant declarations, which specify objects of a specific sort whose meaning is fixed throughout the proof. Global constant declarations are signaled by the keyword given, while axioms are simply stated without justification. Every free object identifier in an axiom must be a previously declared global constant.
In the text proper we also encounter two main kinds of statements: formulas together with their justifications and introductions of names for objects. (Introductions of object identifiers are signified by the keywords let and consider, to be introduced later.) Labels name formulas. Any identifier can be introduced more than once as a name of an object. As our creative capabilities when inventing identifiers are usually limited, we tend to repeat identifiers for different purposes in different places of the text. In MIZAR, unlike in many programming languages, the same identifier can be freely reused to denote two different things even in the same place. The following text is correct.
environ
given A being A;
A: A[A] implies not A[A];
begin
not A[A] by A == Mizar is skillful enough to see it.
The principle is simple: identifiers naming different kinds of objects are never in conflict. Therefore, in the same place you can use the same identifier, in our case A, to name: a constant (or a bound variable, but not both), a sort, a formula, and a predicate.
The text encompassed by now and end forms a new scope of identifiers. Any identifier (say a label) introduced in the reasoning overrides the same identifier introduced outside the reasoning and renders the original identifier inaccessible in the reasoning. (We hope that you are comfortable with scoping rules for some programming language.)
Suppose that you are at some line 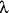in a text.
The general method for determining what formulas and object identifiers are
visible at line 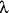is as follows:
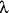are those
associated with syntactically complete statements that appear in
their entirety before line .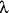
.
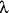Nothing appearing in the justification of a formula is visible outside
the justification.
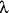introduces an
object identifier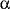 
, then only those formulas that do not have
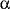free in them are properly visible.
We put the qualification---properly---as the formulas may be visible with the
confusion between the two 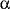s completely unclear to the human reader
(and the writer as well).
The following example illustrates visibility with respect to formulas:
environ
A1: P[] implies Q[];
A2: P[] or not R[];
A3: not R[] implies S[];
begin
== At this point A1, A2, A3 are all visible
1: now
== At this point A1, A2, A3 are all visible, but 1 is not,
== as the statement it labels is not completed yet.
== 2, 3 are not visible because they follow this point
assume 2: not P[];
3: not R[] by A2, 2;
== At this point, 2 and 3 are now visible.
thus S[] by 3,A3;
end;
not P[] implies S[] by 1;
== At this point A1, A2, A3, and 1 are all visible.
== 2, 3 are not because they are inside a justification.
4: now
assume 5: R[];
6: now
assume 7: P[];
thus R[] by 5;
end;
8: now
== A1, A2, A3, 1, 5, and 6 are visible.
== 7 is not because it is inside a justification.
== 4 is not because we are inside the `formula` it
== labels.
assume 9: not P[];
thus R[] by 5;
end;
thus (P[] implies R[]) & (not P[] implies R[]) by 6,8;
end;
R[] implies (P[] implies R[]) & (not P[] implies R[]) by 4;
== This next statement redefines A1, so the previous
== formula referred to by A1 is no longer visible.
A1: not R[] or R[];
environ == Note the empty environment.
begin
1: now
assume A: (P[] implies Q[]) & (not P[] implies Q[]);
1: P[] or not P[]; == Excluded Middle
2: P[] implies Q[] by A; == CE
3: not P[] implies Q[] by A; == CE
4: (P[] or not P[]) implies Q[] by 1, 2, 3; == Case Analysis
thus Q[] by 1, 4; == MP
end;
( (P[] implies Q[]) & (not P[] implies Q[]) ) implies Q[] by 1 == II
Here is an example that proves that
implies
always has the same logical value as
or
Thus, we prove that the two formulas are equivalent.
environ
given today being DAY;
begin
one_way: now
assume A: Raining[today] implies Cloudy[today];
1: Raining[today] or not Raining[today]; == Excluded Middle
2: now
assume A2: not Raining[today];
thus not Raining[today] or Cloudy[today] by A2; == DI
end;
3: now
assume A3: Raining[today];
3a: Cloudy[today] by A, A3; == MP
thus not Raining[today] or Cloudy[today] by 3a; == DI
end;
thus not Raining[today] or Cloudy[today] by 1,2,3; == Case Analysis
end;
other_way: now
assume B: not Raining[today] or Cloudy[today];
1': now
assume B1: Raining[today];
thus Cloudy[today] by B, B1; == More DE
end;
thus Raining[today] implies Cloudy[today] by 1' == II
end;
(Raining[today] implies Cloudy[today])
iff
not Raining[today] or Cloudy[today]
by one_way, other_way == EqI
Note how we have made references to distributed formulas above. We save space by not recording the compact versions of the formulas that will be obtained from the reasonings labelled one_way and other_way applying the II rule. The compact formula is needed in a conclusion, thus we have to apply the the II rule at one point.
Here is another example:
environ
given S being STUDENT;
given M being Money;
begin
1': now
assume A:( Need[M] implies Work[S] & Save[M] );
1: now
assume A1: Need[M];
1a: Work[S] & Save[M] by A, A1; == IE
thus Work[S] by 1a; == CE
end; == Do you see what we have demonstrated?
2: now
assume A1: not Save[M];
2a: now
assume A2: Need[M];
2b: Work[S] & Save[M] by A, A2; == IE
thus Save[M] by 2b; == CE
end; == Do you see what we have demonstrated?
thus not Need[M] by A1, 2a; == MT
end; == Do you see what we have demonstrated?
1': Need[M] implies Work[S] by 1; == II
2': not Save[M] implies not Need[M] by 2; == II
thus (Need[M] implies Work[S]) & (not Save[M] implies not Need[M])
by 1', 2'; == CI
end;
(Need[M] implies Work[S] & Save[M])
implies
(Need[M] implies Work[S]) & (not Save[M] implies not Need[M])
by 1' == II
Of course MIZAR's knowledge of propositional logic makes all of these example steps unnecessary, and that is why step 2a in the proof above could be abbreviated. We go into such detail with these simple proofs only to illustrate how the inference rules work, not to indicate that this is how you should do a complex proof---it is simply that the details of a complex proof get in the way of understanding the basic inferences.