It is said that this step function is Lorentz invariant because it only distinguishes between the past and the future, which is a Lorentz invariant concept. Show that this step function is Lorentz invariant.
Hint: I believe this is true only if ![]() is restricted to be
a time-like vector.
is restricted to be
a time-like vector.
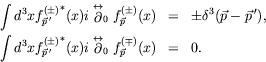
is satisfied for a solution to the Klein-Gordon equation,
![]() , that is a superposition of negative energy plane-wave
solutions.
, that is a superposition of negative energy plane-wave
solutions.
reduces to the proper nonrelativistic expression in the nonrelativistic limit.
Show that the
![]() are orthonormalized.
are orthonormalized.
The
![]() are defined as
are defined as
and the
![]() ,
where
,
where
![]() are general scalar functions of the
magnitude of
are general scalar functions of the
magnitude of ![]() .
Derive the normalization requirement for
.
Derive the normalization requirement for
![]() .
.
to obtain experessions for
![]() and
and
![]() .
.
where
![]() ,
,
![]() ,
,
![]() , and
, and
![]() .
.
Look for solutions that are finite at ![]() and
and ![]() and show that
and show that
where ![]() is
is ![]() or a positive integer and
or a positive integer and ![]() is the
non-negative solution of
is the
non-negative solution of
Show the energy can be expanded in powers of ![]() and to order
and to order
![]() is
is
where
![]() is the total quantum number and can take on
positive integer values.
Identify the rest energy, the energy in the nonrelativistic theory and
the fine-structure energy.
Calculate the spread of the fine-structure levels for a given
is the total quantum number and can take on
positive integer values.
Identify the rest energy, the energy in the nonrelativistic theory and
the fine-structure energy.
Calculate the spread of the fine-structure levels for a given ![]() .
(Note: they are much larger than obeserved experimentally in the
hydrogen spectrum.)
.
(Note: they are much larger than obeserved experimentally in the
hydrogen spectrum.)
Show that without loss of generality ![]() .
.
-
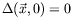 ,
,
-
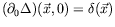 ,
,
-
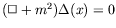 ,
,
-
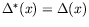 ,
,
-
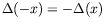 ,
,
-
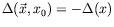 ,
,
-
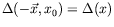 ,
,
-
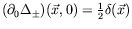 .
.
and thus show that
![\begin{displaymath}
E = m\left[ 1 +
\frac{Z^2\alpha^2}{(n-l-\frac{1}{2}+\sqrt{(l+\frac{1}{2})^2 -
Z^2\alpha^2})^2} \right]^{-\frac{1}{2}}
\end{displaymath}](img960.png)
- Show that the ground state energy for any mesonic atom heavier than
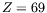 is complex.
Explain what this complex energy means.
is complex.
Explain what this complex energy means.
- Mesonic atoms have been well studied at places like Los Alamos and it
has been found that the ground states of atoms as heavy as lead
(
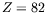 ) or uranium (
) or uranium (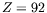 ) are quite stable.
How do you reconcile this fact with the result obtained above?
Be as quantitative as you can.
) are quite stable.
How do you reconcile this fact with the result obtained above?
Be as quantitative as you can.
and show that
Suggestion: Use as an interaction potential the usual form
where
Utilize normalized plane waves solutions of the Klein-Gordon equation
and simple first order perturbation theory
and show that you get positive- and negative-energy solutions.
Show that the Schrödinger equation is not Lorentz invariant.