Coulomb Interaction

Consider the Coulomb interaction

$$A_0 = -\frac{Ze}{r}\quad \textrm{and}\quad \vec{A} = 0$$ (4.156)

and the substitution

$$\hat{p}_\mu \rightarrow \hat{p}_\mu - \frac{e}{c} A_\mu .$$ (4.157)

The Klein-Gordon equation with a Coulomb potential is

$$\left[(i\hbar\partial^\mu - \frac{e}{c}A^\mu)^2 - m^2c^2\right]\Phi = 0 ,$$

$$\left[(i\hbar\partial_0 - \frac{e}{c}A_0)^2 - (-i\hbar\vec{\nabla} - \frac{e}{c}\vec{A})^2 - m^2c^2\right]\Phi = 0 ,$$

$$\left[(i\hbar\partial_t -eA_0)^2 + \hbar^2c^2\nabla^2 - m^2c^4\right]\Phi = 0 .$$ (4.158)

For stationary states $\Phi = e^{-iEt/\hbar}\phi(\vec{x})$ we can write

$$\left( E + \frac{Ze^2}{r} \right)^2\phi + (\hbar^2c^2\nabla^2 - m^2c^4)\phi = 0 .$$ (4.159)

For spherical coordinates

$$\nabla^2 = \frac{1}{r^2} \frac{\partial}{\partial r} \left( ... ... \frac{1}{r^2\sin^2\theta} \frac{\partial^2}{\partial\phi^2} ,$$ (4.160)

$$\phi(r,\theta,\phi) = R(r) Y_l^m(\theta,\phi) .$$ (4.161)

$$\Rightarrow \nabla^2 = \frac{1}{r^2} \frac{d}{dr} \left( r^2 \frac{d}{dr} \right) - \frac{l(l+1)}{r^2} ,$$ (4.162)

where $l = 0,1,2,...$. The Klein-Gordon equation in spherical coordinates is

$$\left[ \frac{(E+Ze^2/r)^2 - m^2c^4}{\hbar^2c^2} \right]R = \... ...left( r^2\frac{d}{dr} \right) + \frac{l(l+1)}{r^2} \right] R .$$ (4.163)

$$\frac{1}{r^2} \frac{d}{dr} \left( r^2\frac{dR}{dr} \right) +... ...ac{Z^2e^4}{\hbar^2c^2r^2} - \frac{l(l+1)}{r^2} \right] R = 0 .$$ (4.164)

Defining $\frac{E^2-m^2c^4}{\hbar^2c^2} \equiv -\frac{\alpha^2}{4}$ we can write

$$\frac{1}{r^2} \frac{d}{dr} \left( r^2\frac{dR}{dr} \right) ... ...c^2\alpha^2r^2} + \frac{4l(l+1)}{\alpha^2r^2} \right] R = 0 .$$ (4.165)

Defining $\gamma \equiv \frac{Ze^2}{\hbar c}$ we can write

$$\frac{1}{r^2} \frac{d}{dr} \left( r^2\frac{dR}{dr} \right) ... ...ha^2r} - 4\frac{\gamma^2-l(l+1)}{\alpha^2r^2} \right] R = 0 .$$ (4.166)

Defining $\lambda \equiv \frac{2E\gamma}{\hbar c\alpha}$ we can write

$$\frac{1}{r^2} \frac{d}{dr} \left( r^2\frac{dR}{dr} \right) - \frac{\alpha^2}{4} \left[ 1 - \frac{4\lambda}{\alpha r} - 4\frac{\gamma^2-l(l+1)}{(\alpha r)^2} \right] R = 0 ,$$

$$\frac{1}{r^2} \frac{d}{dr} \left( r^2\frac{dR}{dr} \right) + \alpha^2 \left[ \frac{\lambda}{\alpha r} - \frac{1}{4} - \frac{l(l+1)-\gamma^2}{(\alpha r)^2} \right] R = 0 .$$ (4.167)

Defining $\rho \equiv \alpha r$ and $\frac{d}{dr} = \frac{d\rho}{dr}\frac{d}{d\rho} = \alpha\frac{d}{d\rho}$

$$\frac{\alpha^2}{\rho^2} \alpha \frac{d}{d\rho} \left( \frac{\rho^... ...[ \frac{\lambda}{\rho} - \frac{1}{4} - \frac{l(l+1)-\gamma^2}{\rho^2} \right] R = 0 ,$$

$$\frac{1}{\rho^2} \frac{d}{d\rho} \left( \rho^2\frac{dR}{d\rho} \r... ...[ \frac{\lambda}{\rho} - \frac{1}{4} - \frac{l(l+1)-\gamma^2}{\rho^2} \right] R = 0 .$$ (4.168)

This radial equation is the same as in the nonrelativistic case if $l(l+1)\rightarrow l(l+1) - \gamma^2$. Solving for $E$ we have

$$\frac{E^2-m^2c^4}{\hbar^2c^2} = -\frac{1}{4} \left( \frac{2E\gamma}{\hbar c\lambda} \right)^2$$

$$E^2 - m^2c^4 = -\frac{E^2\gamma^2}{\lambda^2}$$

$$E^2\left(1+\frac{\gamma^2}{\lambda^2}\right) = m^2c^4$$

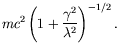$$E = mc^2\left( 1 + \frac{\gamma^2}{\lambda^2} \right)^{-1/2} .$$ (4.169)

The parameter $\lambda$ is determined by the boundary condition on $R$ when $\rho = \infty$.

The remainder of this problem is left as an exersize for the student.