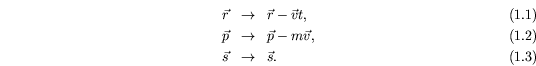
The Schrödinger equation can be derived using the correspondence principle from the Hamiltonian formalism of nonrelativistic classical mechanics. The equation will have all the invariance principles of the Hamiltonian from which it is derived. For an isolated system, the Schorödinger equation will be invariant under spatial rotations and translations. It will also be invariant under a Galilean transformation:
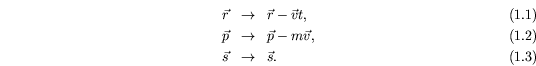
In other words, the Schrödinger equation is invariant under a
change of reference system if the relative velocity, ![]() ,
between the reference systems is small.
It is however not invariant under a general Lorentz transformation.
,
between the reference systems is small.
It is however not invariant under a general Lorentz transformation.
Nonrelativistic quantum mechanics can thus only describe phenomena
for ![]() .
It can not describe phenomena concerning the interaction between light
and matter, for example, the emission, absorption, or scattering of
photons.
.
It can not describe phenomena concerning the interaction between light
and matter, for example, the emission, absorption, or scattering of
photons.
This course thus embarks on the journey of relativistic quantum mechanics. Surprisingly this will not be the end of the journey, since there is a difficulty with relativistic quantum mechanics in that the ``law of the conservation of the number of particles'' ceases, in general, to be true. Because of the equivalence of mass and energy, particles can be created or absorbed whenever the interaction gives rise to energy transfers above the rest mass of the particles. To describe these dynamical states and number, requires us to journey into the concepts of quantized fields, otherwise known as quantum field theory.