Charge of a Klein-Gordon Particle

If two real wave functions $\phi_1(x)$ and $\phi_2(x)$ separately satisfy a Klein-Gordon equation with the same mass $m=m_1=m_2$, then the separate Klein-Gordon equations can be replaced by one Klein-Gordon equation for a complex wave function:

$$\phi(x) = \frac{1}{\sqrt{2}} \left[\phi_1(x) \pm i\phi_2(x)\right] .$$ (4.50)

Using the definition of charge in equation 4.49, we see that $\phi$ and $\phi*$ have opposite charge and that a real wave function has zero charge. In general we have

complex scalar fields are charged,

real scalar fields are uncharged.

We now examine the charge for a superposition of positive-energy and superposition of negative-energy solutions to the Klein-Gordon equation. If $f_p^{(+)}(x)$ is a positive-energy solution to the Klein-Gordon equation with momentum $p$, the superposition of all such positive-energy solutions is

$$\phi^{(+)}(x) = \int d^3p a_+(p)f_p^{(+)}(x) ,$$ (4.51)

where $a_+(p)$ is a weighting function of three-momentum only and $f_p^{(+)}(x)$ is given by equation 4.19. The charge for this general positive-energy solution is

$$Q = i\int d^3x{\phi^{(+)}}^*(x) \stackrel{\leftrightarrow} {\partial}_0\phi^{(+)}(x)$$

$$= i \int d^3xd^3pd^3p^\prime a_+^*(p)a_+(p^\prime) {f_p^{(+)}}^*(x) \stackrel{\leftrightarrow}{\partial}_0 f_{p\prime}^{(+)}(x)$$

$$= \int \frac{d^3xd^3pd^3p^\prime}{(2\pi)^3} \frac{E+E^\prime}{2\sqr... ...*(p)a_+(p^\prime) e^{it(E-E^\prime)} e^{-i\vec{x}\cdot(\vec{p}-\vec{p}^\prime)}$$

$$= \int d^3pd^3p^\prime \frac{E+E^\prime}{2\sqrt{EE^\prime}} a_+^*(p)a_+(p^\prime) \delta^3 (\vec{p}-\vec{p}^{\:\prime}) e^{it(E-E^\prime)}$$

$$= \int d^3p\vert a_+(p)\vert^2 > 0 ,$$ (4.52)

where the last step follows because $\vec{p}=\vec{p}^{\:\prime}$ implies $E=E^\prime$.

For a superposition of negative-energy solutions, $Q = -\int d^3p\vert a_-(p)\vert^2 < 0$. Thus $\phi^{(+)}(x)$ specifies a particle with positive charge and $\phi^{(-)}(x)$ a particle with the same mass but negative charge.

For zero charge spin-0 particles, the wave function $\phi(x)$ must be real: $\phi^*(x)=\phi(x)$. For a single momentum we can write

$$\phi^{(0)}(x) = \frac{1}{\sqrt{2}} [f^{(+)}_{\vec{p}}(x) + f^{(-)}_{-\vec{p}}(x)] ,$$

$$= \frac{1}{\sqrt{2}} \left[ \frac{1}{(2\pi)^{3/2}} \frac{1}{\sqrt{2... ...rac{1}{(2\pi)^{3/2}} \frac{1}{\sqrt{2E}}e^{i(Et-\vec{p}\cdot\vec{x})} \right] ,$$

$$= \frac{1}{(2\pi)^{3/2}} \frac{1}{\sqrt{2E}} \frac{2}{\sqrt{2}}\frac{[e^{-i(Et-\vec{p}\cdot\vec{x})} + e^{i(Et-\vec{p}\cdot\vec{x})}]}{2} ,$$

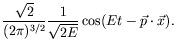$$= \frac{\sqrt{2}}{(2\pi)^{3/2}}\frac{1}{\sqrt{2E}} \cos(Et-\vec{p}\cdot\vec{x}) .$$ (4.53)

From the relativistic wave equation for spin-0 particles and the interpretation of its wave functions, we are lead to three solutions which correspond to the electric charges $+$, $-$ and $0$ for every momentum $\vec{p}$. The relativistic quantum theory thus reveals the charge degree of freedom of particles.

According to our current understanding, there are no fundamental spin-0 particles. However, if we do not probe the internal structure of mesons they can be considered as Klein-Gordon particles. For the pion system $(\pi^+,\pi^0,\pi^-)$ with the approximation that each state has the same mass, we write (by convention)

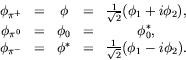$$\begin{array}{ccccc} \phi_{\pi^+} & = & \phi & = & \frac{1}{... ...phi^* & = & \frac{1}{\sqrt{2}} (\phi_1 - i\phi_2) . \end{array}$$ (4.54)

By convention it is the positive-charged boson which is the particle and the negative-charge fermion which is the particle.