J Pharm Pharmaceut Sci (www.ualberta.ca/~csps) 2(3):92-98, 1999
Application of Direct Search Optimization for Pharmacokinetic Parameter Estimation
Received manuscript October 5th, 1999; Revised November 29th, 1999; Accepted November 30th, 1999.
Farhad
Khorasheh1,
Amir Mahbod Ahmadi, and Abbas Gerayeli
Department
of Chemical Engineering, Sharif University of Technology, Tehran, Iran
Department of Pharmacy and Pharmaceutical Sciences, University of Alberta, Canada
PDF Version for printing
Abstract
Purpose. For simple pharmacokinetic compartmental models, analytical solution to the governing differential equations along with common graphical methods provide a mean to evaluate the associated rate constants. These graphical methods, however, can not be used for the more complex multi-compartment models. Furthermore, parameter estimation using slope and intercept values from the graphical methods is often accompanied with error. In this study a numerical solution is applied for the solution of the governing differential equations and a simple direct search optimization procedure utilizing random numbers is used for pharmacokinetic parameter estimation. Method. The methodology is demonstrated with reference to experimental literature data for ciprofloxacin and ofloxacin whose pharmacokinetic behavior has been reported in terms of a two-compartment model. Results. Examination of the predicted drug concentrations from the graphical method and the optimization methodology indicate that both methods have comparable accuracy in predicting the drug concentrations. The graphical method, however, only shows good accuracy in the early stages both after i.v. and oral drug administration whereas the optimization procedure, due to the nature of the objective function formulation, provides good accuracy over the entire range of times after drug administration. Conclusions. The methodology is simple, provides optimized parameters which accurately predict drug concentrations, and is flexible to include more weight on the early-time data or be extended to multi-compartment models.
Introduction
Pharmacokinetic models are used to describe drug absorption, distribution, and elimination in human and animal body. In these models, the body is described in terms of one or more compartments to and from which drugs could be absorbed, transferred, and eliminated according to simple kinetic rate expressions. These expressions result in one or more ordinary differential equations with time as the independent variable. The solution to these equations would give the drug concentration in each compartment as a function of time. For the simple single-compartment and two-compartment models, analytical solutions for the governing differential equations are readily available and simple graphical techniques can be used for pharmacokinetic parameter estimation. These graphical methods, however, are only applicable for simple models and can not be used for the more complex multi-compartment models. Furthermore, parameter estimation using slope and intercept values from the graphical methods is often accompanied with error. In this study a numerical solution is applied for the solution of the governing differential equations and a simple direct search optimization procedure utilizing random numbers is used for pharmacokinetic parameter estimation. This methodology is demonstrated with reference to experimental literature data for ciprofloxacin and ofloxacin. The pharmacokinetic behavior of these antibacterial drugs which belong to the flouroquinolones family has been reported in terms of two-compartment models.
Single Compartment Models
Compartmental models have been used extensively to describe the time course of drugs in the body. The simplest of such models is the single compartment model. Drug elimination from this compartment is represented by a first order elimination rate constant,
kE. In the case of an i.v. dose, the drug concentration in the compartment (plasma concentration) is given by the following expression:
where C0 is the initial drug concentration and C is the drug concentration in the plasma which could be measured experimentally from blood samples taken at different times. In the case where administration of drug into the central compartment is via infusion with a zero order rate constant, the following expression is obtained:
For an oral dose, absorption of drug into the central compartment is usually represented by a first order absorption rate constant, ka, and analytical solution to the governing differential equations results in the following expression for the drug concentration:
where VC is the volume of the central compartment and XD is the drug dose. Pharmacokinetic parameters for the single compartment models can be estimated from the experimental drug concentration as a function of time, C, using common graphical procedures outlined elsewhere (1).
Multi-Compartment Models
In multi-compartment pharmacokinetic models, the body is considered in terms of two or more compartments including a central compartment. Distribution of drug can occur in all compartments whereas absorption and elimination is usually considered for the central compartment only. Although various multi-compartment models have been proposed (1), the pharmacokinetic behavior of most drugs can be represented by single or two compartment models. For the two compartment model with an i.v. bolus dose, the governing differential equations and associated initial conditions are as follows:
where C1,max is the initial drug concentration in the central compartment after i.v. bolus dose and C1 and C2 are the drug concentration in the central and second compartment, respectively. The equations for a two compartment model with an oral dose are similar except that an additional term involving drug absorption in to the central compartment is considered with a first order absorption constant ka. The governing differential equations and associated initial conditions are as follows:
where Vd is the drug volume of distribution. Analytical solution results in the following expressions for the drug concentration in the central compartment:
Equation (11) is for an i.v. bolus dose and equation (12) is for an oral dose. The parameters, for example L, M, N, a, b, and ka in the case of an oral dose, are combinations of various pharmacokinetic rate constants (kE, ka, k12, and k21) and can be obtained from the slope and intercept values of semilog plots of drug concentration versus time using the Residual Method as outlined elsewhere (1). A shortcoming of this method is the error that can be associated with the estimated parameter values specially when there is some scatter in the experimental data. Here a methodology is developed to obtain optimized model parameters which minimizes an objective function defined as the sum of squares of deviations between predicted and experimental drug concentrations in the central compartment. Predicted values are obtained by numerical solution of the governing differential equations using the fourth order classical Runge-Kutta method (2). The optimization method is based on a direct search algorithm with systematic reduction of the search region (3).
Pharmacokinetic Parameter Estimation using Direct Search Optimization
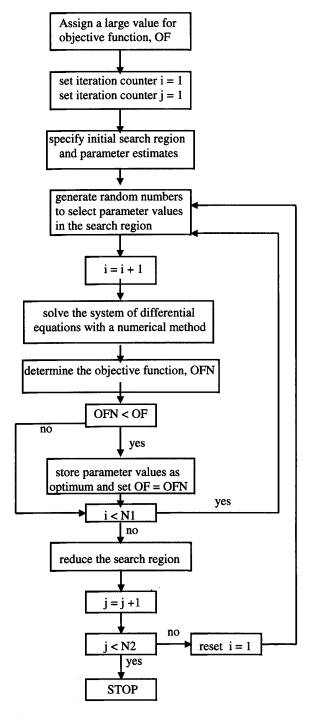
The flowchart of the direct search optimization algorithm for pharmacokinetic parameter estimation is presented in Figure 1. Initially, an upper and lower bound for each parameter is specified. The lower bound for non-negative rate constants is taken as zero. The upper bound can be specified by an arbitrary high value that covers the range of values typically reported in the literature. The mid point for each parameter range is taken as the initial estimate of the optimum parameter values. Determination of the optimum parameters within the specified search region proceeds by selecting a parameter value from each range using random numbers. The governing differential equations are then solved numerically using the randomly selected parameters to obtain the drug concentration in the central compartment at different times.
Figure 1. Flowchart of the optimization algorithm for parameter estimation
For this purpose, the fourth order classical Runge-Kutta method (2) with a step size of 0.01 hour is used. The predicted drug concentrations are used to evaluate an objective function for optimization which is formulated as follows:
where Ci,exp and Ci,calc are the experimental and predicted drug concentration in the central compartment, respectively, and P is the number of experimental measurements. The optimum parameter values are those which minimize the above objective function. The algorithm proceeds by another random selection of parameters from the search regions and subsequent evaluation of the objective function. The procedure is repeated N1 times and the set of parameters which results in the least value for the objective function is stored as the optimum set for the search region. The proposed value for N1 is between 100 and 500 (3) and in this study 100 is used. The above procedure is repeated after a reduction of the search region; the range for each parameter is reduced by a factor of (1-e). The proposed value for e is between 0.005 and 0.05 (3) and in this study a value of 0.05 is used. The number of reductions of the search region, N2, used in this study was 200.
Results
The above algorithm was applied for analysis of available clinical data for ciprofloxacin and ofloxacin whose pharmacokinetic behavior have been reported in terms of a two compartment model (4-10). The available data which are reported in Figures 2 and 3 for ciprofloxacin and ofloxacin, respectively, represent i.v. and oral doses for healthy adults and children as well as adults with respiratory problems. The pharmacokinetic parameters obtained from both the graphical method and the methodology described in this work are summarized in Table I.
Figure 2. Ciprofloxacin concentration in the central compartment for healthy adults after a) 400 mg i.v. bolus dose, b) 500 mg oral dose, and c) 250 mg oral dose. In all the figures, filled triangles represent experimental data obtained from clinical studies reported in the literature. Hollow squares with solid lines represent the predicted values of drug concentration in the central compartment using pharmacokinetic parameters that are obtained by common graphical methods (1). Hollow circles and dotted lines represent predicted values of drug concentration in the central compartment using pharmacokinetic parameters that are obtained by the methodology described in this study.
Figure 3. Ofloxacin concentration in the the central compartment after a) 200 mg i.v. bolus dose for patients with respiratory problems, b) 185 mg i.v. bolus dose for children, c) 185 mg oral dose for children, and d) 200 mg oral dose for healthy adults.
Discussion
Examination of Figures 2 and
3
indicate that both the graphical method and the procedure outlined in
this paper have comparable accuracy in predicting the drug concentration
in the central compartment. In most cases, the graphical method only
shows good accuracy in predicting the drug concentration in the early
stages both after i.v. and oral administration of drug whereas the
procedure described in the paper provides good agreement between
predicted and experimental drug concentration over the entire range of
times after drug administration as indicated by significantly lower
values of the objective function (Table I) for this method as compared
with those for the graphical method. The value of the objective function
provides a measure of deviations between predicted and experimental drug
concentrations. The lower the value of the objective function, the more
accurate are the predicted drug concentrations. In the methodology
described in this paper, the optimized pharmacokinetic parameters are
those which minimize the objective function. Since in the formulation of
the objective function experimental points are included in both the
early and late stages after drug administration, the optimized model
parameters provide accurate predictions over the entire range of times
after drug administration.
Table
I. Summary of the pharmacokinetic parameters estimated from experimental
data.
a) i.v. bolus doses
|
Figure # |
kE
(h-1 ) |
k12
(h-1 ) |
k21
(h-1 ) |
OF1 |
|
2(a) |
0.464 [0.398] |
0.843 [1.011] |
0.907 [1.037] |
0.080 [0.110]2 |
|
3(a) |
0.174 [0.192] |
0.320 [0.256] |
0.546 [0.304] |
0.075 [2.510] |
|
3(b) |
0.277 [0.254] |
0.347 [0.286] |
0.431 [0.494] |
0.017 [0.129] |
b) oral doses
|
Figure # |
kE
(h-1 ) |
k12
(h-1 ) |
k21
(h-1 ) |
ka
(h-1 ) |
OF |
|
2(c) |
0.628 [0.857] |
0.844 [0.781] |
0.301 [0.442] |
0.984 [2.128] |
0.073 [0.187] |
|
2(b) |
0.290 [0.241] |
0.233 [0.357] |
0.320 [0.747] |
1.489 [1.721] |
0.047 [0.163] |
|
3(c) |
0.039 [0.262] |
0.316 [0.124] |
0.027 [0.217] |
0.841 [1.161] |
0.355 [0.880] |
|
3(d) |
0.208 [0.242] |
1.010 [0.204] |
2.550 [0.261] |
1.117 [1.276] |
0.019 [0.760] |
1
OF is the calculated value of the objective function.
2 Values inside brackets are obtained from the graphical method (1) and those outside brackets are obtained from the optimization algorithm in this work.
where Wiís are the weighting factors specified for each data point. The results presented in Table I and Figures 2 and 3 represent an objective function with Wi = 1 for all data points. If one wishes to place more weight on the early time data, the corresponding Wi for early time experimental points could be set at a higher value (for example 5). In such a case the optimized parameters would result in very accurate prediction in the early stages at the expense of a loss in accuracy of the predicted concentrations in the late stages. This flexibility is a major advantage of the methodology described in this paper over common graphical methods. Furthermore, the present methodology can be very simply extended to the more complex multi-compartment models.
In the case of oral administration, an important parameter is the drug volume of distribution, Vd. As can be seen from equation (10), an important parameter which has to be specified in the optimization procedure is the initial condition C0 = XD F/Vd at t = 0. The reported literature value for bioavalability, F, for ofloxacin and ciprofloxacin was 0.6 and 0.95, respectively. Since the drug dose in oral administration is specified for each experiment, the value of the optimized parameters and the corresponding objective function value would depend on the specified value of Vd. In the case of i.v. doses, the initial condition that has to be specified (equation 6) is C1 = C1,max at t = 0 where C1,max is the initial drug concentration in the central compartment after an i.v. dose which is taken as the first plasma concentration immediately after an i.v. dose. Figure 4 indicates that in the case of ofloxacin, the optimum value for Vd which provides the least value for the objective function, the best estimation, is about 39 liter for adults and 21 liter for children.
Figure 4. Objective function value versus volume of distribution for a) 200 mg dose of ofloxacin for healthy adults, and b) 185 mg oral dose of ofloxacin for children.
The implementation of the above methodology in a computer program is
quite straight forward. Two subroutines would be required; a subroutine
for random number generation which is available for most programming
languages, and a subroutine as a differential equation solver using a
numerical method. If such a differential equation solver is not available
as a package, a simple explicit Runge Kutta method (2) for solving the
governing initial value problem can be employed. Runge Kutta methods (2)
are quite simple and an algorithm along with a computer program is readily
available in many numerical methods texts. As indicated above, the
parameter optimization is performed by a random search in specified
parameter ranges with a reduction in the size of the search region at
subsequent steps. To implement this strategy two loops are necessary; an
outer loop which specifies the size of the search region, and an inner
loop in which parameter selection is made at random. The above
optimization algorithm is quite simple to implement but requires a large
computation effort; 20000 combinations of parameters are tested.
Conclusions
In this paper an optimization procedure was applied for estimation of pharmacokinetic parameters for compartmental models. The methodology is quite simple and provides optimized parameters which accurately predict drug concentrations in the central compartment over the entire range of time after both i.v. and oral drug administration.
Acknowledgments
The financial support for this work was provided by the research administration of Sharif University of Technology.
References
-
G. Gibaldi. Pharmacokinetics, Marcel Decker, New York, 1984.
-
G. F. Gerald and P. O. Wheatley. Applied Numerical Analysis, Addison-Wesley, New York, 1994.
-
R. Luus and T. H. I. Jaackola. Optimization by direct search and systematic reduction of the search region. AIChE J. 19: 760-766 (1973).
-
M. Neuman. Clinical pharmacokinetics of the newer antibacterial 4-quinolones. Clin. Pharmacokin. 14: 96-121 (1988).
-
D. C. Brittain, B. E. Scully, M. J. McElrath, R. Steinman, P. Labthavikul, and H. C. Neu. The pharmacokinetics and serum and urine bactericidal activity of ciprofloxacin. J. Clin. Pharmacol. 25: 82-88 (1985).
-
D. E. Nix, M. Spivey, A. Norman, and G. G. Schentag. Dose-ranging pharmacokinetic study of ciprofloxacin after 200-, 300-, and 400-mg intraveneous doses. The Annals of Pharmacotherapy. 26: 8-10 (1992).
-
J. T. Lettieri, M. C. Rogge, L. Kaiser, R. M. Echols, and A. T. Heller. Pharmacokinetic profiles of ciprofloxacin after single intravenous and oral doses. Antimicrobial Agents and Chemotherapy. 36: 993-996 (1992).
-
K. Vance-Bryan, D. R. P. Guay, and J. C. Rotschafer. Clinical pharmacokinetics of ciprofloxacin. Clin. Pharmacokinet. 19: 434-461 (1990).
-
D. B. Bethell, N. P. J. Day., N. M. Dung, H. T. N. Minh, C. McMulli, N. T. M. Linh, N. Q. Dong, H. Vinh, A. P. MacGowan, L. O. White, and N. J. White. Pharmacokinetics of oral and intravenous ofloxacin in children with multidrug-resistant typhoid fever. J. Antimicrobial Agents and Chemotherapy. 40: 2167-2172 (1996).
-
R. Farinotti, J. H. Trouvin, V. Bocquet, N. Vermerie, and C. Carbon. Pharmacokinetics of ofloxacin after single and multiple intravenous infusions in healthy subjects. J. Antimicrobial Agents and Chemotherapy. 32: 1590-1592 (1988).
Corresponding Author: Farhad Khorasheh, Department of Chemical Engineering, Sharif University of Technology, Tehran, Iran, khorashe@che.sharif.ac.ir
Keywords: pharmacokinetics; compartmental models; parameter optimization; direct search.
Published by the Canadian Society for Pharmaceutical Sciences.
Copyright © 1998 by the Canadian Society for Pharmaceutical Sciences.
http://www.ualberta.ca/~csps
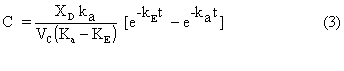
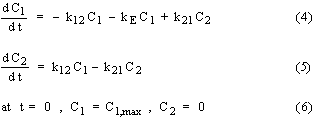
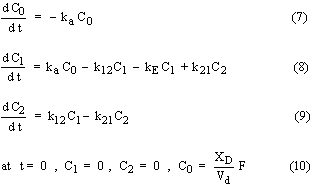
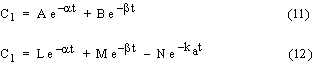
/F.Khorasheh/Figure4.jpg)