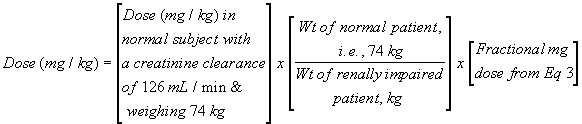Pharmacokinetics Tricks and Traps: Drug Dosage Adjustment in Renal Failure Received manuscript January 2nd, 1999; Accepted February 13th, 1999. Harold Boxenbaum1, Stacey Tannenbaum, Michael Mayersohn Frederick Oleson Consider a drug that is not bound to blood components, completely eliminated by the kidneys, and for which drug clearance is directly proportional to creatinine clearance. Inasmuch as there are no metabolites, pharmacodynamic activity and toxicity, either directly or indirectly, will be related to plasma concentrations. Assume a representative 80 kg patient with a creatinine clearance of 140 mL/min receives a maintenance dose of 400 mg Q 12 h. Assuming one wishes to keep the dosing interval constant, and simultaneously maintain the same average steady-state plasma concentration, what will be the appropriate maintenance dose for a 50 kg renally impaired patient having a creatinine clearance of 70 mL/min? Based on the ratio of raw creatinine clearances (70 mL/min vs. 140 mL/min), the dose would be 200 mg Q 12 h. However, based on comparative mg/kg doses, the renally impaired subject would receive 80% the mg/kg dose of the patient with normal renal function (4.0 vs. 5.0 mg/kg Q 12 h, respectively). Although somewhat counter-intuitive, this latter calculation is correct, primarily because the "renally impaired" subject is not renally impaired at all. Although common to define mild renal impairment in terms of a creatinine clearance between 50-80 mL/min, this categorization fails to consider body weight as a necessary co-variable. Dosage adjustment in renally impaired subjects need therefore be discussed in terms of both absolute (mg) and weight-adjusted (mg/kg) doses. An additional aspect of data analysis in renal failure studies that unfortunately has received little attention pertains to adjustment of creatinine clearance for body surface area, usually through normalization to 1.73 m2 body surface area. Although intuitively appealing, this practice is superfluous. The simplest and most commonly employed equation relating drug clearance to creatinine clearance is:
where CL is drug clearance, a is a proportionality constant, CLCr is creatinine clearance and CLNR is non-renal drug clearance. A plot, such as illustrated in Figure 1, is often used to estimate drug clearance as a function of renal status, where creatinine clearance is either measured or calculated from serum creatinine (see Cockcroft and Gault (1) for widely used equations for estimating creatinine clearance from serum creatinine). As illustrated in Figure 1, two independent variables commonly utilized are:
However, there is no a priori reason to adjust units of creatinine clearance for body surface area or any other normalization factor, since factors correlating with or impacting on creatinine clearance are just as likely to affect drug clearance in an analogous fashion. Hence, abscissa and ordinate volume/time units simultaneously and tacitly adjust for clearance correlates such as body surface area, and there is no need to adjust creatinine clearance any further, e.g., by normalizing to a 1.73 m2 body surface area. In a linear system (assumed throughout), average steady-state drug plasma concentration is given by Wagner et al (2): where Cav is average steady-state drug plasma concentration, F is absolute bioavailability, t is dosage interval, and CL is clearance. It is apparent that Cav is directly proportional to rate of dosing (FD/t ) and inversely related to CL. Assuming rate of dosing remains unaltered, Cav will change if CL changes, as in renal impairment for a drug eliminated by the kidneys. One primary principle utilized for dosage adjustment (reduction) in renal failure, therefore, is to reduce rate of dosing in such a manner that the ratio of rate of dosing to CL is the same as in normal patients. This will then result in Cav values remaining unchanged in normal vs. renally impaired subjects. As suggested above, to maintain a fixed Cav, rate of dosing in renally impaired patients need only be reduced by the same percentage as the reduction in drug CL. Consequently, the adjusted dose in a renally impaired subject is calculated as the ratio of drug CL in that subject to that of a normal, non-renally impaired subject, viz.: where the subscript RI refers to a renally impaired subject, and the subscript N refers to a normal subject. For example, assume the following values in a normal subject: a = 0.1, CLCr = 126 mL/min, and CLNR = 1.5 mL/min; for the renally impaired subject, assume CLCr drops to 30 mL/min, and, since they are fixed parameters, a and CLNR remain the same. Consequently the renally impaired subject would receive 31.9% of the normal dose (expressed in terms of amount, e.g., mg). Assuming the normal population has a mean weight of 74 kg, the appropriate equation for calculation of mg/kg doses in renally impaired subjects is:
Assume the dose for a normal patient (without renal impairment) is 8 mg/kg, and the weight of the renally impaired patient is 55 kg. The fractional mg dose calculated above is 31.9%. Substitution into Eq. 4 gives a dose of 3.43 mg/kg (where the dosing interval remains unchanged). Four quick notes:
References
Corresponding author: Harold Boxenbaum, Arishel Inc., 14621 Settlers Landing Way, North Potomac, Maryland, 20878-4305, USA, email:shelbyb@ix.netcom.com Published by the Canadian Society for Pharmaceutical Sciences. Copyright © 1998 by the Canadian Society for Pharmaceutical Sciences. |