Graphing correlations is quite useful for quickly visualizing which climate variables are significant for a tree ring series. From our correlations of precipitation and temperature it seemed apparent that summer temperatures had the highest influence on ring width. This is expected as growing season temperature is likely the primary growth limiting variable at high latitudes (Chapin et al 2000, Körner and Paulsen 2004). Unlike temperature variables, precipitation did not seem to follow a coherent pattern. Running the PCA with the temperature variables did not reveal any new trends and only acted to complicate the interpretation of this simple example.
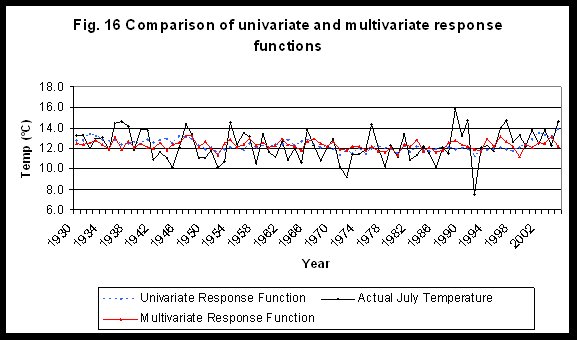
As useful as simple correlations are, they cannot be used to include many variables into our model simultaneously. By simply retaining July temperatures and ignoring the rest of the data, we lose a great deal of interannual variation in our model. This is especially apparent when we compare our univariate response function (Fig. 9) to the plot of ring width variation and July temperatures (Fig. 10). Although we are comparing July temperatures to a dimensionless ring width index, it is apparent the rind width index has better agreement to the actual July temperatures than does our univariate response function.
By deriving a response function using even one principle component, which is still an optimized combination of our original variables, I hoped to better explain and predict the trend in the data. This appears to be the case when I compare the principle component multivariate function with the univariate function (Fig. 16). July temperatures are in slightly better agreement with the multivariate function and the multivariate function appears to have greater interannual variation.
Interestingly, the principle component which is retained from the MR is the second principle component. The original temperature variables which load highly on this component (Fig. 13) are the growing season months with the greatest standard deviation, namely April and May (Fig. 12). September and October temperature are also important for this component and possibly therefore this component can be interpreted as relating to growing season length. As an aside it can be noted that temperatures during the fall and spring are determined to some extent by the degree of cloud cover and precipitation. Even though we separated out our precipitation variables in the beginning, by no means should it suggest that precipitation is not relevant to tree growth, however its influence may largely be captured in the temperature signal.
Likely the multivariate model would have shown better improvement over the univariate model if the variables that had the highest original correlations also had the highest standard deviation (or interannual variation). This would have made fewer of the original variables significant for the first principle component, and this component would have accounted for a greater proportion of the total variance. Presumably the regression model would be far more accurate and its interpretation in terms of the measured variables would be more straightforward. Ideally, this set of hypothetical variables would also be those relevant to the study. In terms of climate change, this may be winter temperatures as opposed to growing season length. In reality, though, it is likely we cannot count on these best case scenarios. Paying close attention to all the available univariate and multivariate statistics may make judging the validity of the derived model easier.
In many ways multivariate statistics are an absolutely necessity in tree ring studies. They help identify patterns in the data, and provide a means of reducing the complexity of many variables. Similarily important, however often over-looked, are the univariate statistics. If from comparison it is revealed both univariate and multivariate techniques provide similar results, it is likely that a clear climate growth relationship cannot be easily modeled using a single combination of the available variables.
In order for me to understand what is normal for climate and tree ring relationships, far more chronologies will have to be studied. However, this preliminary exercise with tree rings was an instructive first step in preparing me to assess whether or not ring width variation found in shrubs can also be related to climate with some degree of certainty.