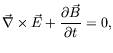 |
(7.88) | ||
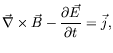 |
Maxwell's equations of classical electrodynamics in vacuum are
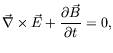 |
(7.88) | ||
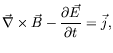 |
where we are using Heaviside-Lorentz (rationalized Gaussian) units.
Defining
![]() and
and
![]() , the
four-vector potential is related to the electric and magnetic fields
by
, the
four-vector potential is related to the electric and magnetic fields
by
| (7.89) |
Further, we can show that in terms of the antisymmetric field strength tensor
| (7.90) |
that Maxwell's equations now take the compact form
| (7.91) |
and current conservation,
![]() , follows as a natural
compatibility condition.
, follows as a natural
compatibility condition.
These equations are equivalent to the following covariant equation for
![]() .
.
| (7.92) |
which is general and ![]() is in the presence of charge and currents.
is in the presence of charge and currents.
![]() and
and ![]() are unchanged by the gauge transformation
are unchanged by the gauge transformation
| (7.93) |
where ![]() is any scaler function of
is any scaler function of ![]() .
We use this freedom to pick
.
We use this freedom to pick ![]() so that we can write Maxwell's
equations in the form
so that we can write Maxwell's
equations in the form
| (7.94) |
The requirement
![]() is known as the Lorentz
condition.
The process of choosing a particular condition on
is known as the Lorentz
condition.
The process of choosing a particular condition on ![]() so as to
define it uniquely is called ``choosing a gauge''.
Potentials satisfying
so as to
define it uniquely is called ``choosing a gauge''.
Potentials satisfying
![]() are said to be ``in the
Lorentz gauge''.
However, even after choosing a gauge, there is still some residual
freedom in the choice of the potential
are said to be ``in the
Lorentz gauge''.
However, even after choosing a gauge, there is still some residual
freedom in the choice of the potential ![]() .
We can still make another gauge transformation
.
We can still make another gauge transformation
| (7.95) |
where ![]() is any function that satisfies
is any function that satisfies
| (7.96) |
This last equation ensures that the Lorentz condition is still satisfied.