http://dcwww.fys.dtu.dk/~tbohr/
Joint work with Tomas Bohr (Danish Technical University, Denmark) and Shinya Watanabe (Ibaraki University, Japan).
We derive reduced models of fluid motion when the Reynolds number is relatively large (10-1000), and the fluid moves in a layer of water that is relatively thin, but not so thin that a simple lubrication for the friction approximation will suffice. We are particularly interested in appearance of separation in the boundary layer flow. Our work addresses the region of parameters where the established asymptotic methods (like triple deck theory) is not applicable.
This work was motivated by experiments on a circular hydraulic jump and have resulted in several papers - see my vita. Here I present a picture of a polygonal hydraulic jump which appears when a jet of water impacts a surface. See Eric Marten’s web page for more cool pictures and links.

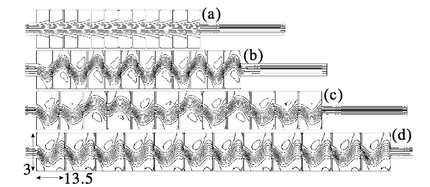
More recent work with Shinya Watanabe treats reduced models in channels with sudden expansions and/or contraction. In particular, we have discovered a new state in a channel with periodically spaced expansions and contractions, that is stationary and yet chaotic: separations go randomly from right to left. For more details, seePhys. Lett A (2007), longer paper is submitted to Fluid Dyn. Research (2007).