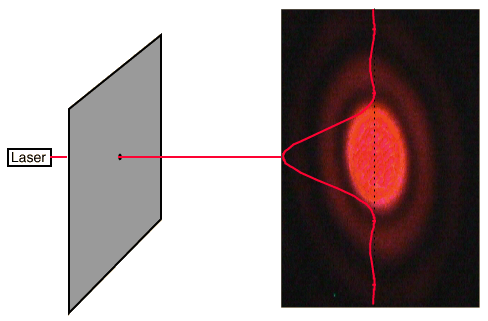
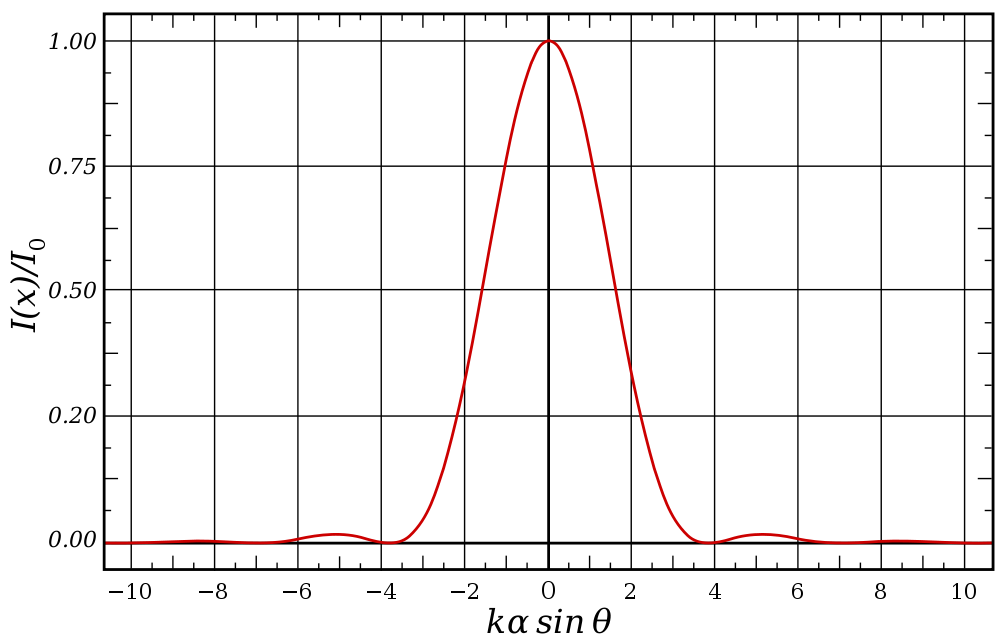
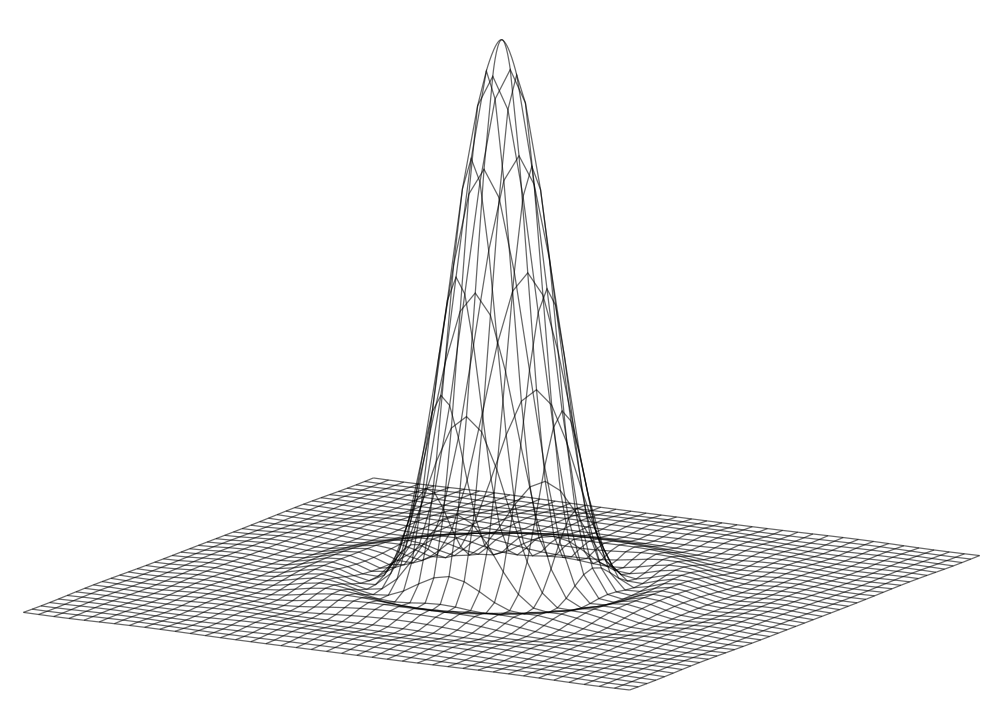
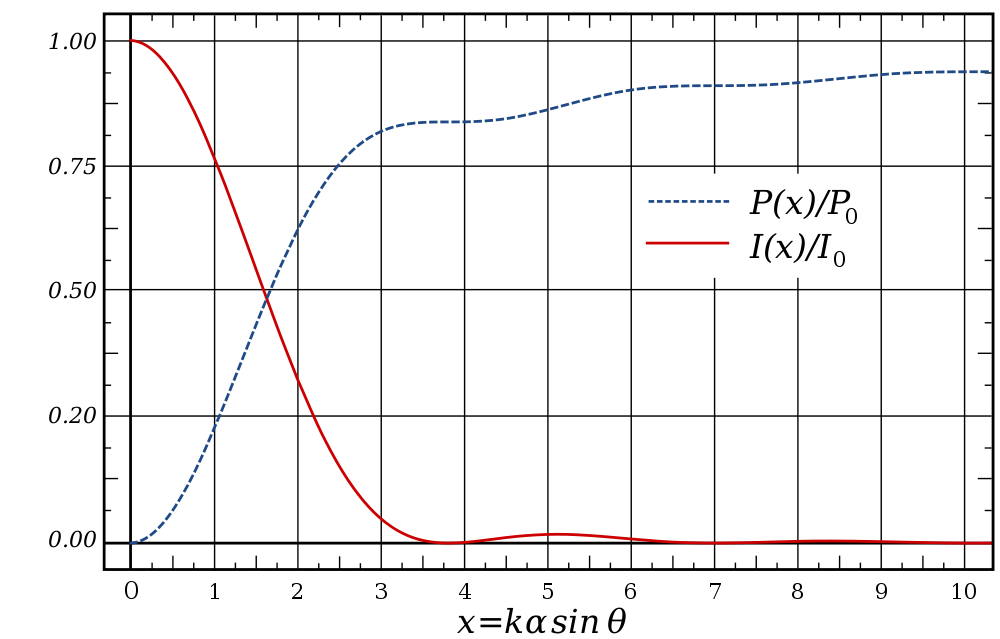
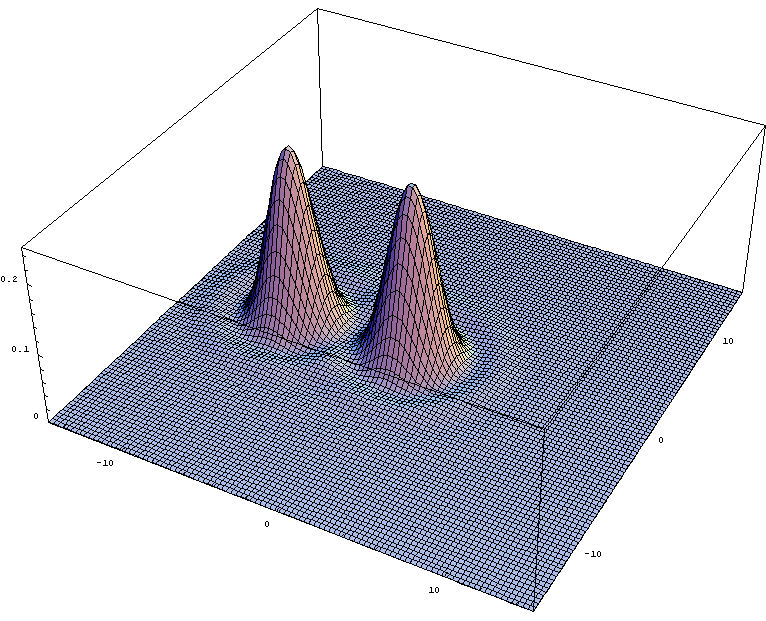
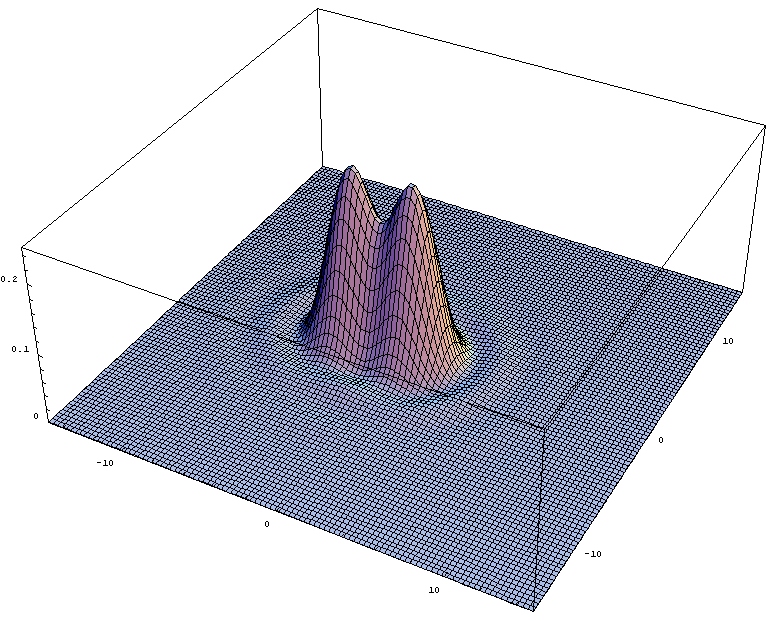
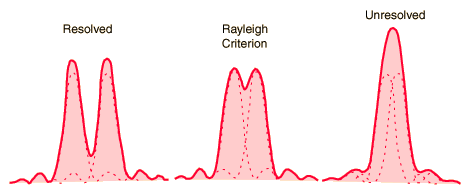
- The case of circular aperture is very important in optical devices. Microscopes, telescopes, cameras, anything utilizes spherical lenses or mirrors are subject to diffraction due to finite size of the aperture through which the light passes.
- Diffraction place fundamental limit on angular resolution of such devices