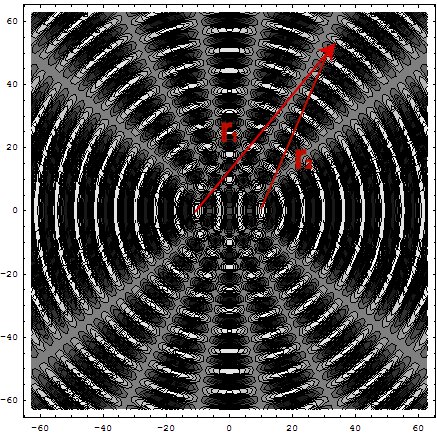
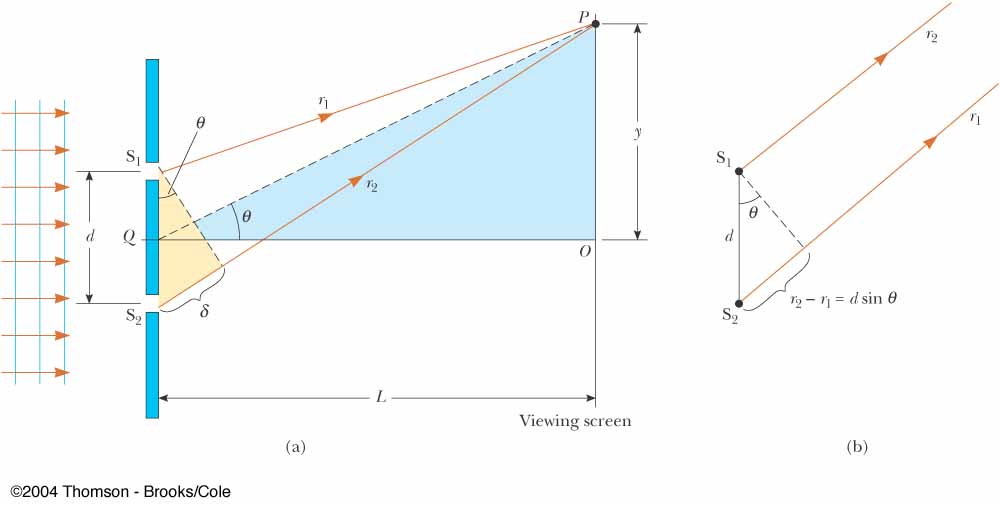
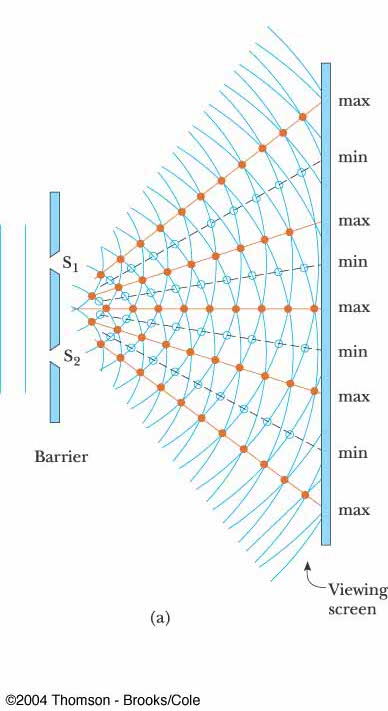
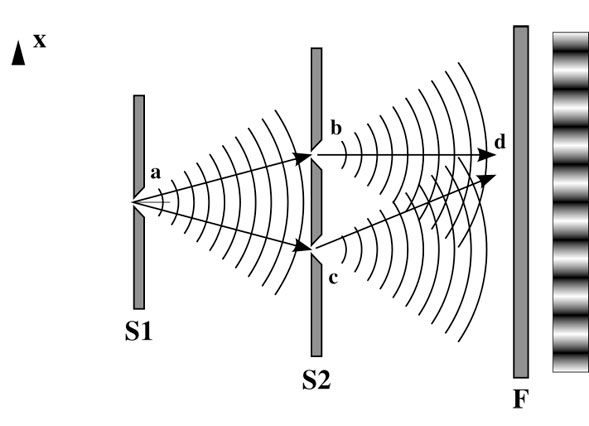
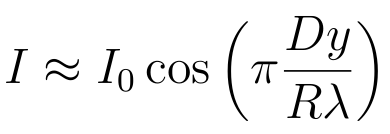- How many antinodal lines this pattern creates ? This
depends on the wavelength of the wave λ
and the distance between the sources D
- It is easy to find out: The maximum paths separation
possible is along the line that connects the sources, and
is equal
( r2 - r1 )max = D
Hence, the maximum possible m that can be
at antinodes is
mmax = int(D/λ)
(int() means take the integer part of the result). So we will
have nodes at
m = 0,± 1, ..., ± mmax
|
|