Lecture 2: Simple Harmonic Motion


Readings: Textbook pages 419-427

Periodic Motion

We call a motion periodic if the state of a system repeats itself after regular time intervals.

  • Periodic (or near periodic) motion is one of the fundamental ways how bodies can move.
  • Indeed, if one has a bound system (e.g - molecule, pendulum) some kind of repetition of the motion is expected with time.
  • The laws of mechanics ensure that if the positions and velocities of a system exactly repeat themselve after some time, subsequent motion will reproduce what was happening before.

There are two main types of periodic motions

Rotation Oscillations (vibrations)
  • Harddrive in this computer
  • Orbiting of planets around stars
  • Electrons in atoms
  • Rotation of the Earth
  • Motion of guitar string
  • Sound (oscillations of air pressure)
  • Vibration of a molecule
  • Ocean waves

Next

Description of the Periodic Motion

  • The time length of one cycle is the period T
  • Reciprocal to the period is the frequency
    f = 1/T
    Frequency tells how many cycles per unit time (seconds) the system undergoes
  • maximum displacement is given by the amplitude A

Flash Player 6 or above is required to view this animation. Please visit http://www.macromedia.com/go/getflashplayer to download Flash


Back Next

Simplest Periodic Motion

The simplest rotational periodic motion (you agree, right ?) is the rotation in circular orbit with velocity of constant magnitude.
  • |V|=const so T = 2 π A/|V|
  • angular velocity ω = d θ / d t where θ is the angle swiped by the radius vector from initial position. ω = |V|/A = const so period T = 2 π / ω
  • ω = 2 π f and is also called angular frequency
  • change of the angle with time is given by integration

More details are in UCalgary app1 and app2

Back Next

Rotation on reference circle and Simple Harmonic Motion

As particles follows uniform rotational motion, its coordinates follow Simple Harmonic Motion (SHM)
x = A cos(θ)     y = A sin(θ)
  • x = A cos(ω t + φ0)
  • Vx = dx/dt
    = -A ω sin(ω t + φ0)
  • ax = dVx/dt
    = -A ω2 cos(ω t + φ0)

in SHM       ax = - ω2 x

Back Next

Harmonic Oscillator

  • Oscillation appear when there is a restoring force that acts on the system when it is out of equilibrium trying to bring it back to equilibrium
  • Consider spring with mass attached, which motion is governed by the Hooke's law m a = F = - k x
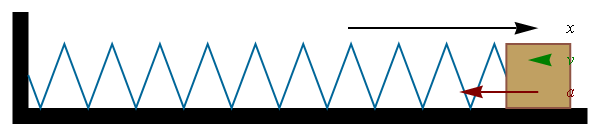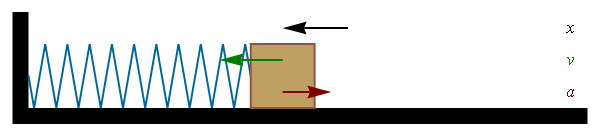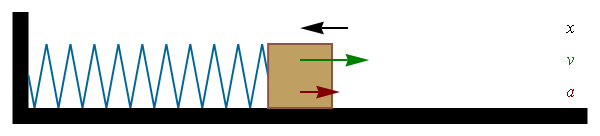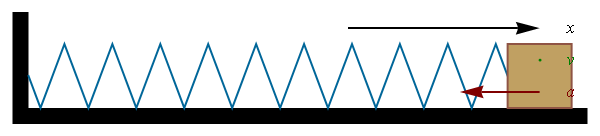
  • How does the mass on the spring moves under Hooke's law ?
  • One can solve differential equation d2 x / d t2 = -(k/m) x , but one can just notice that acceleration is proprtional and opposite to displacement
    a = -(k/m) x

    exactly as it was for SHM !
  • Thus, the mass on the spring experiences SHM
    x = A cos(ω t + φ0) with ω = (k/m)1/2
  • "Initial phase" φ0 depends on what we chose as zero time

Oscillator that follows SHM is called Harmonic Oscillator

Back Next

Properties of a Harmonic Oscillator

  • Displacement, velocity and acceleration - all mechanical properties of the harmonic oscillator are described by simple trigonometric functions with the same one frequency ω
    x = A cos(ω t + φ0)
    v = - A ω sin(ω t + φ0)
    a = -A ω2 cos(ω t + φ0)
  • (angular) frequency of oscillations ω = (k/m)1/2 does not depend how we perturb the oscillator from equilibrium - i.e amplitude. It is determined solely by the internal properties of the system - mass and stiffness of the string. The system has its own frequency ! This is very important concept in physics.
  • Restoring force is proprtional and opposite to displacement F = - α x is a signature of any Harmonic Oscillator .
  • One can play with this applet for another case of Harmonic Oscillator - the mass hanged on a vertical spring in the presense of gravity. Check that such system is harmonic oscillator, and think why
Back