
|


| Example | Animation | Wavefronts shape |
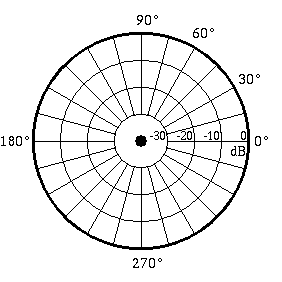
| Monopole, boxed loudspeaker |

|
|
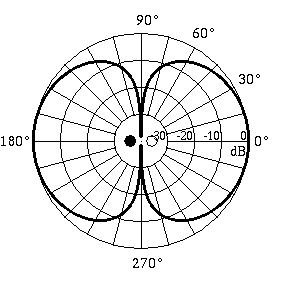
| Dipole, unboxed loudspeaker |

|
|
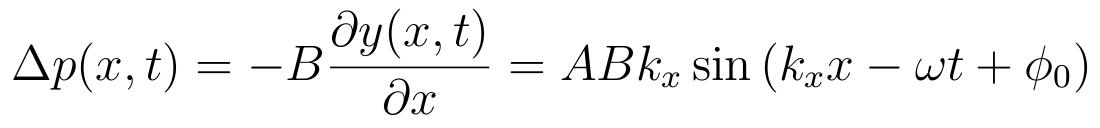
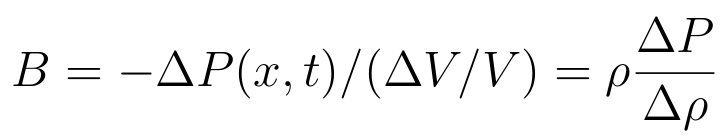 is bulk modulus .
It plays the role of spring constant in Hooke's Law but for
volumetric deformations (strains). Units of bulk modulus are Pascales, as
that for pressure.
is bulk modulus .
It plays the role of spring constant in Hooke's Law but for
volumetric deformations (strains). Units of bulk modulus are Pascales, as
that for pressure.