Lecture 13: Standing Waves; Normal Modes

Standing Waves

• Equation for a standing wave with fixed end at x = 0 y ( x,t ) = 2 A sin( k x ) sin ( ω t)
• Nodes are positioned at x = ½ n λ ,     n=1,2,3,...
• Antinodes are positioned at x = ½ n λ + ¼ λ

What happens if we fix the other end as well ? Like a string in a guitar ?

• From dimensional analysis we suspect that having final length L may interfere with the wavelength of the string. Interplay between L and λ is possible.

• If we do it at the node, where the string does not move, it is not disturbed and continue to oscillate as before with wavelength λ. This happens at L = λ/2, λ, 3λ/2 .... n λ/2

• If we do it at some other place, where the string moves, it can not continue to maintain a standing wave with the wavelength λ - the wavelength does not fit !

Properties of the Normal Modes of a string with fixed ends

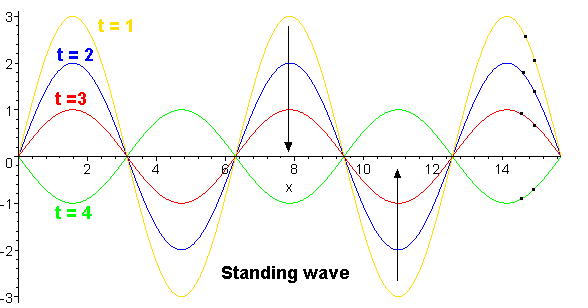
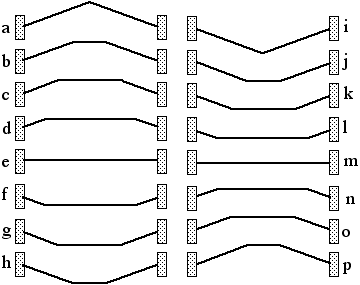
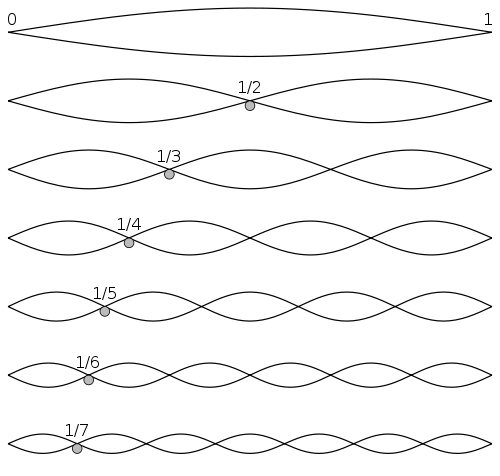
The wavelengths of the normal modes are λn = 2 L, L, 2 L/3, 2L/4 ... 2L/n,    n=1,2,3 ... The general relation between frequency and wavelength λ f = v remains valid Hence, there are normal frequencies as well fn = v/λn = n v /(2L) =              = v/(2L), V/L, 3 v /(2L)... n is the number of antinodes n-1 is the number of nodes besides the end points

• The mode with the longest supported wavelength λ₁ (twice the length of the string ) has the lowest possible frequency f = v/(2L) . It is called the fundamental mode
• Subsequent normal modes have shorter wavelengths (integer fraction of 2L ) and higher frequencies (integer of v/(2L) ). They are called harmonics or, in music, overtones of fundamental mode.

• To confuse things, harmonics and overtones are counted differently. We call fundamental model the first harmonic (i.e just n value), but the first overtone is the second harmonic, fundamental mode in not counted as overtone. I.e harmonic number counts antinodes while overtone number counts nodes in the middle of a string.

• Equation for standing wave with both ends fixed at x = 0 and at x=L y ( x,t ) = 2 A sin( k_n x ) sin ( ω_n t)

Exciting standing waves

Which harmonics are present depends on initial conditions - how the string was excited (say, plucked ? At what place ? Bowed ?) In general, it takes special care to make a pure wave that is just one given harmonics Typically, all harmonics are excited, but with different amplitudes Harmonic analysis of the wave (i.e sound) is the analysis of the distribution of amplitudes between normal modes. Very closely related to Fourier analysis ( expanding waves in Fourier series of normal modes )

More complicated standing waves

• 2D waves of drum vibration can be looked at in detail in drum applet