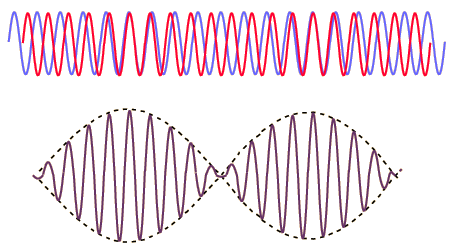
| When waves interfere to add up to a wave of higher amplitude, we speak about constructive interference |
When waves interfere to cancel each other we speak about
destructive interference |
|
|
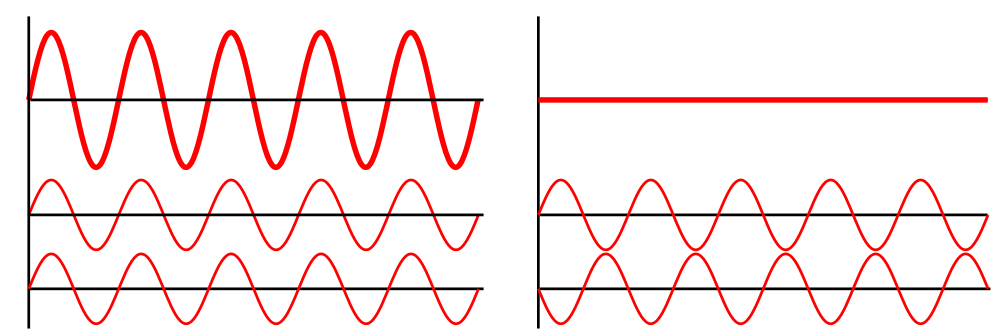
| When waves interfere to add up to a wave of higher amplitude, we speak about constructive interference |
When waves interfere to cancel each other we speak about
destructive interference |

|
|
| One source | Two sources at the same position |
 |
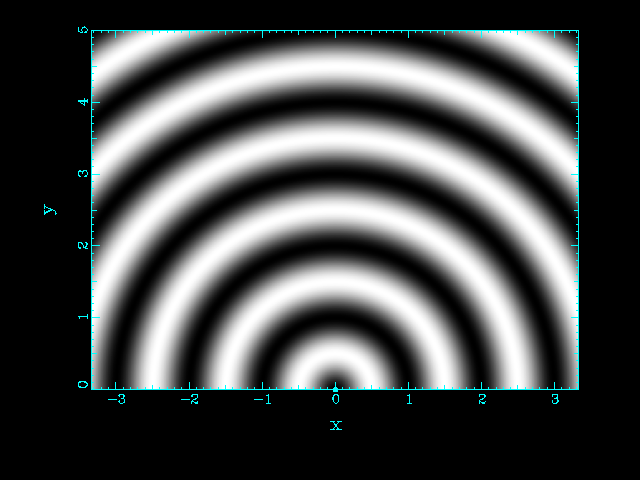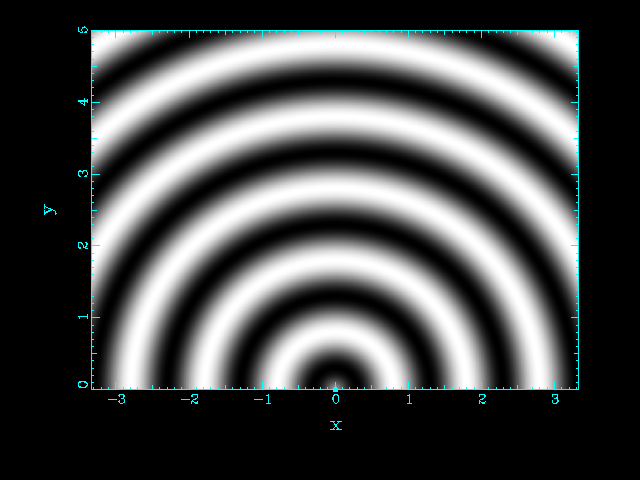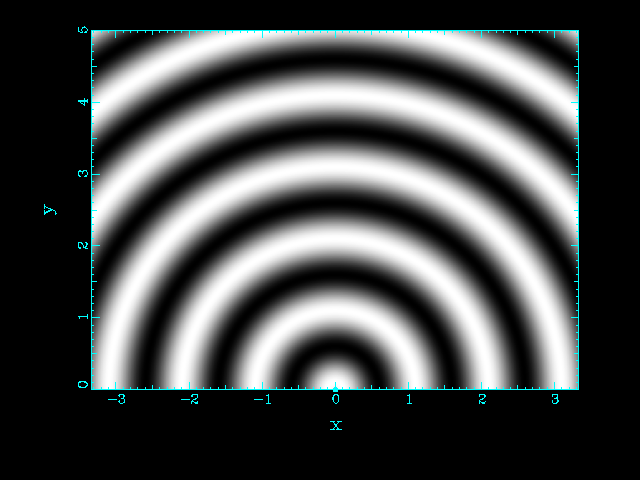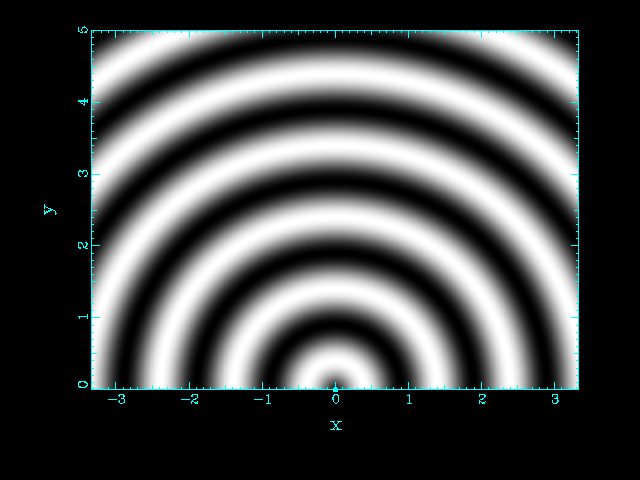 |
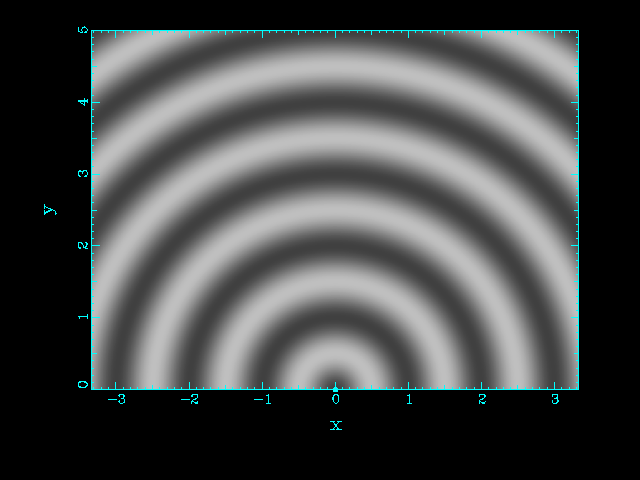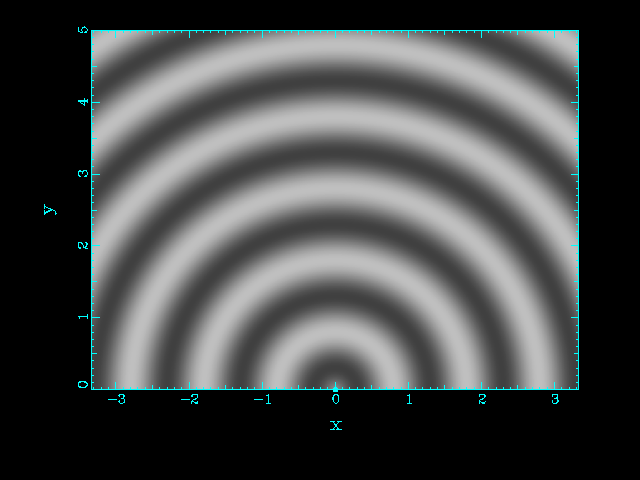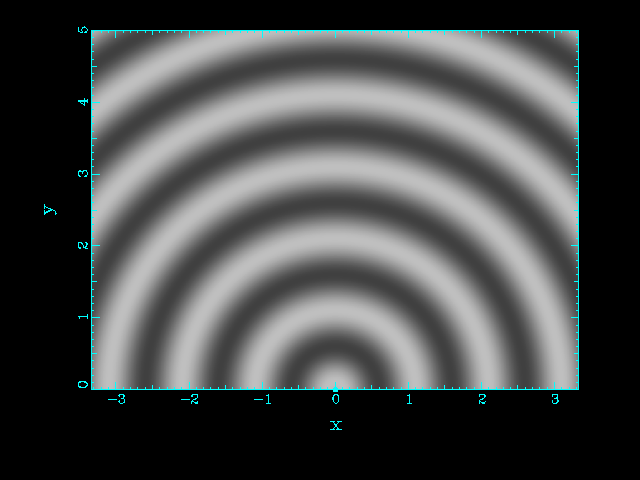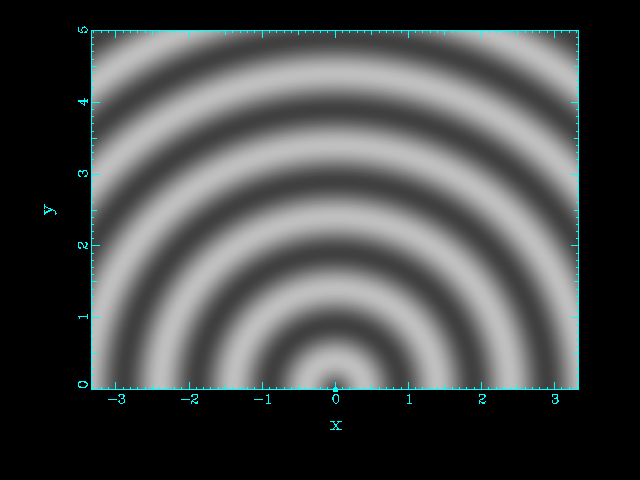
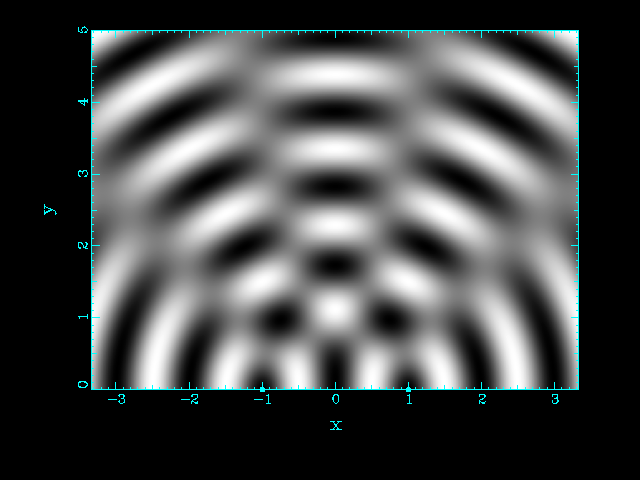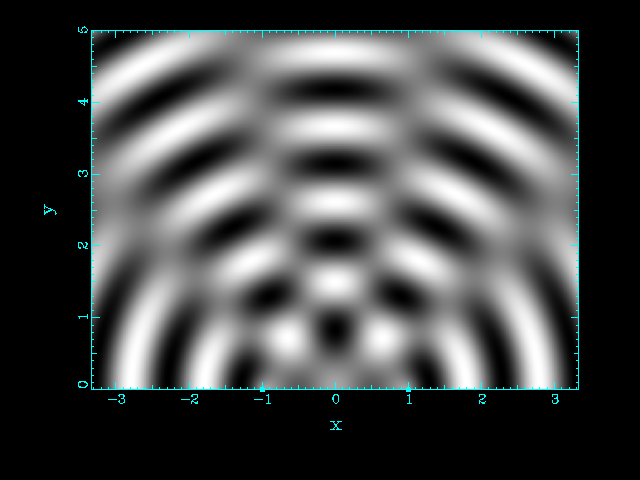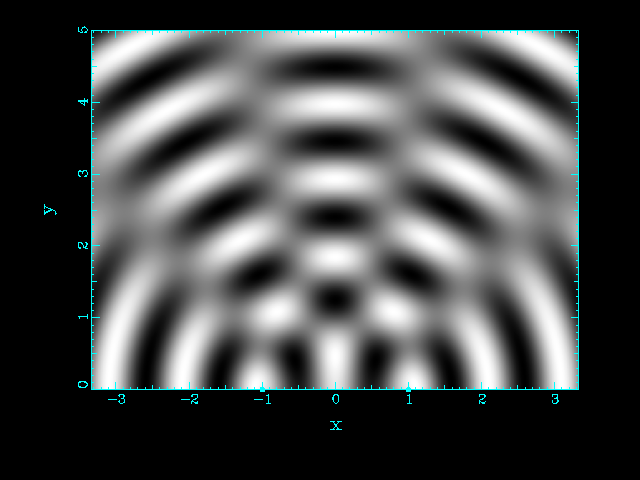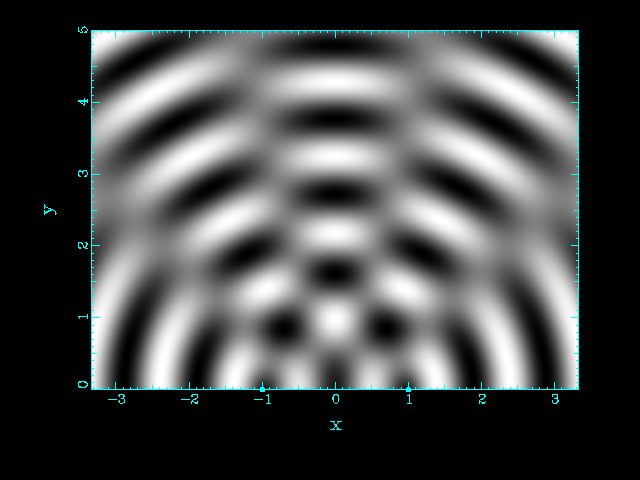
| Two source separated by d = λ | Two source separated by d = 2 λ |
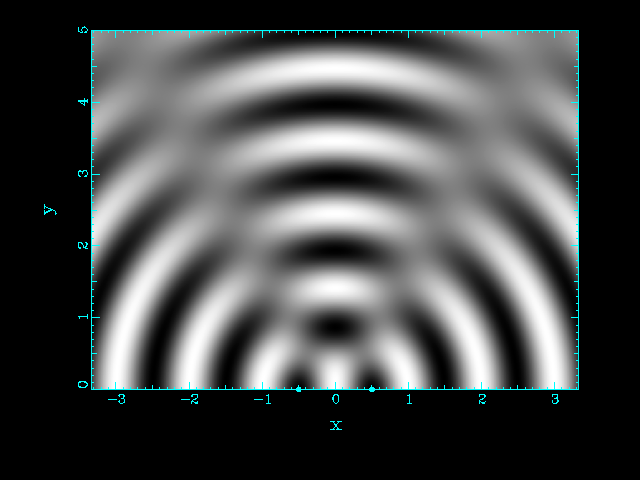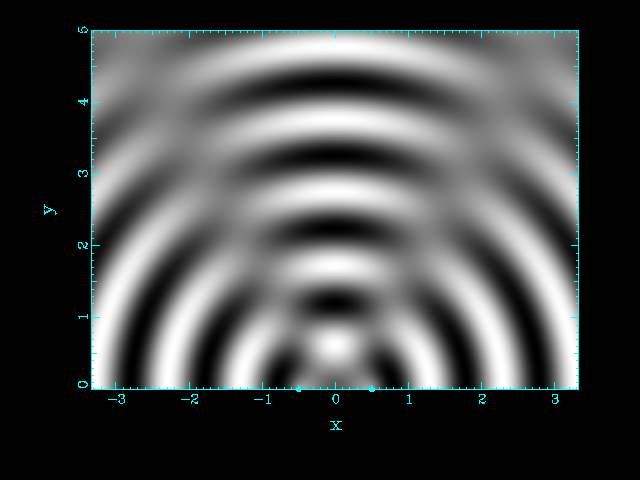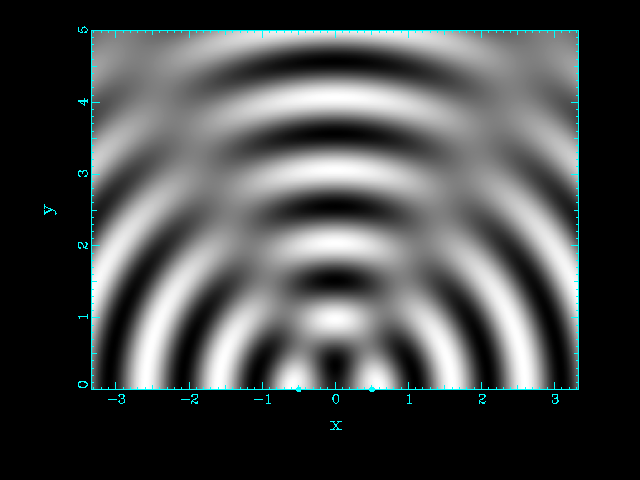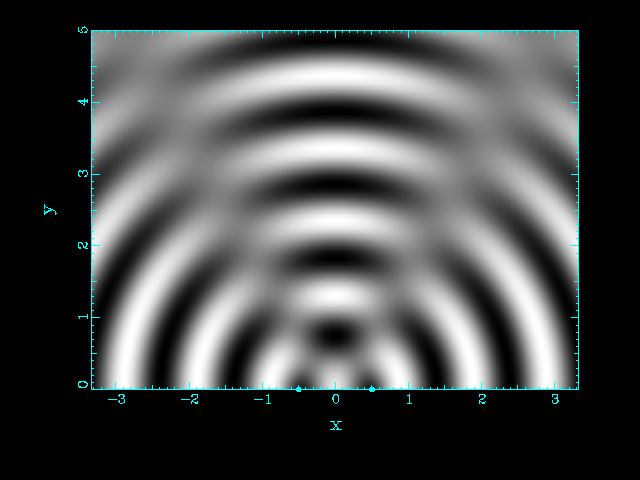 |
 |