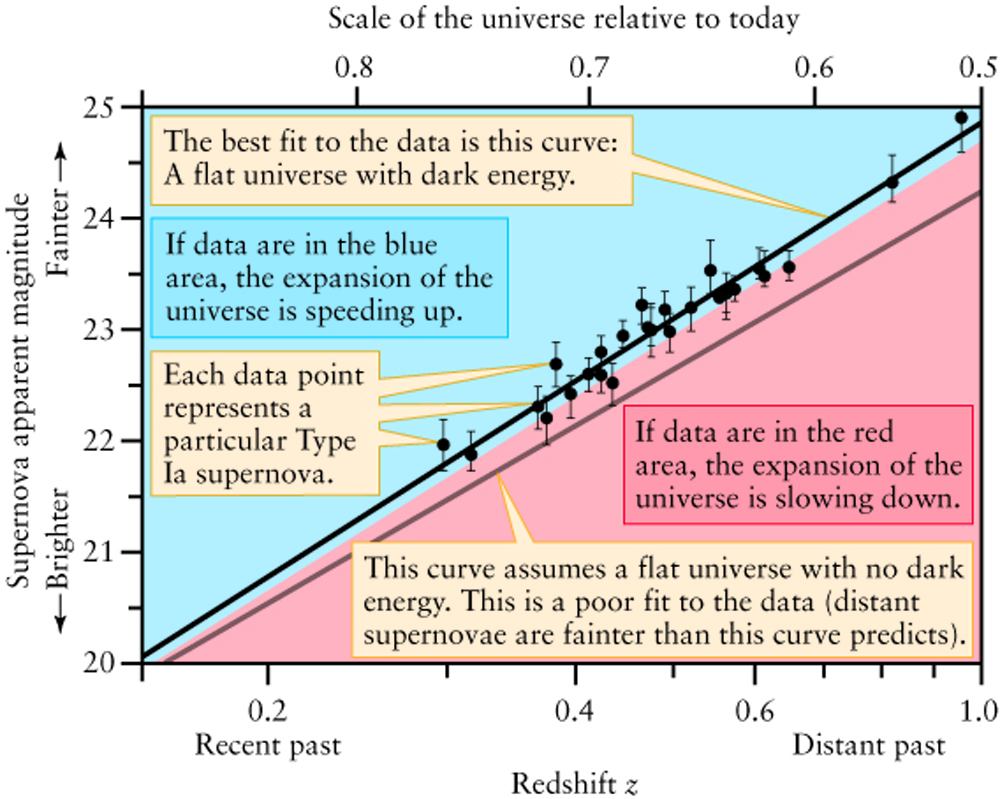
Evidence for Acceleration from Type Ia Supernovae
- The astronomers plotted (M-m) versus redshift (z),
which is equivalent to plotting distance versus velocity.
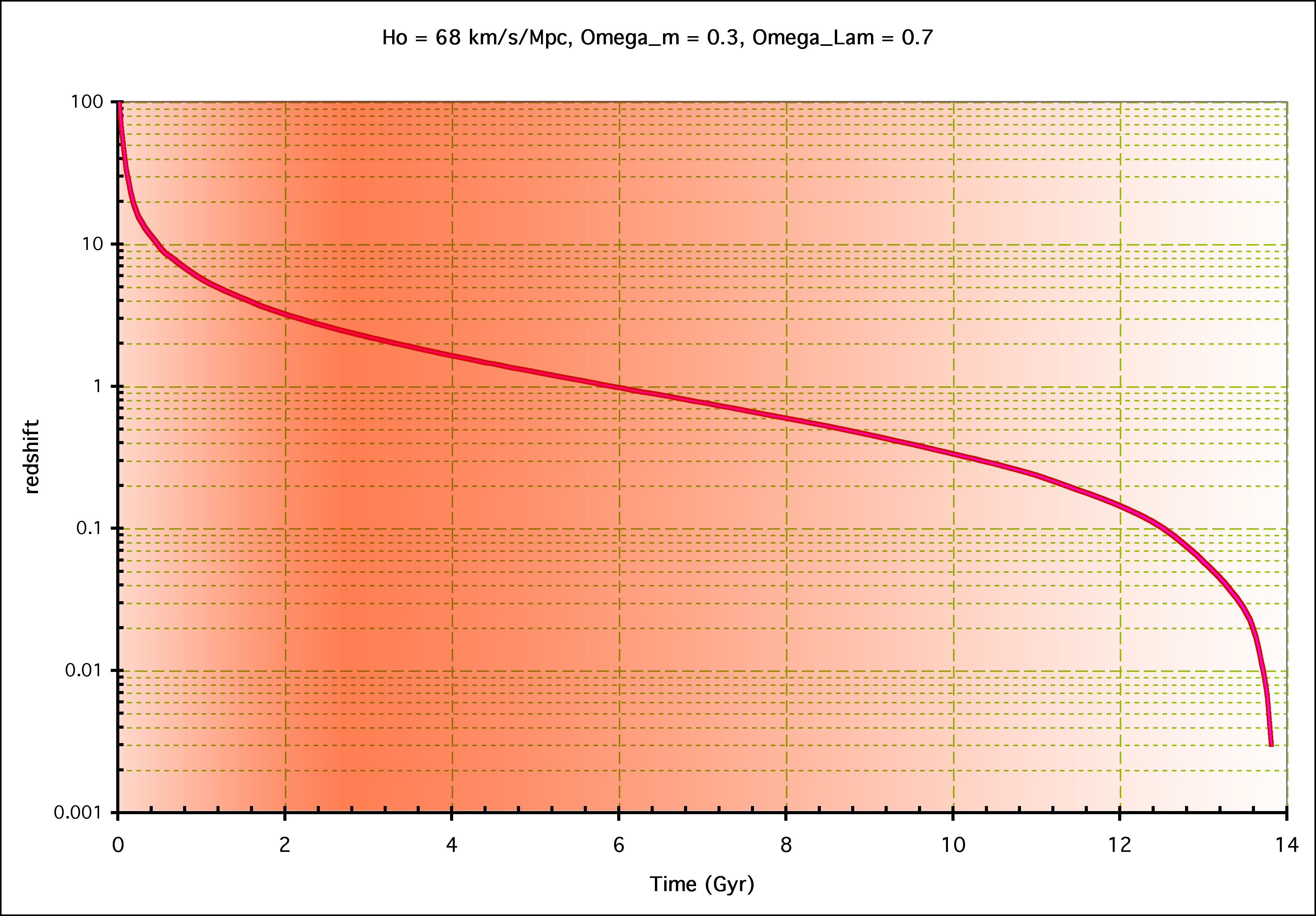
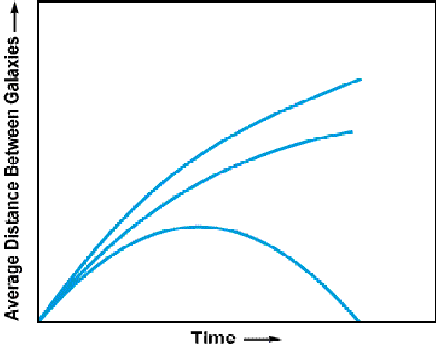
- The data favours a universe whose expansion is
accelerating so that the expansion speed increases with time!
- This is opposite to what was expected!
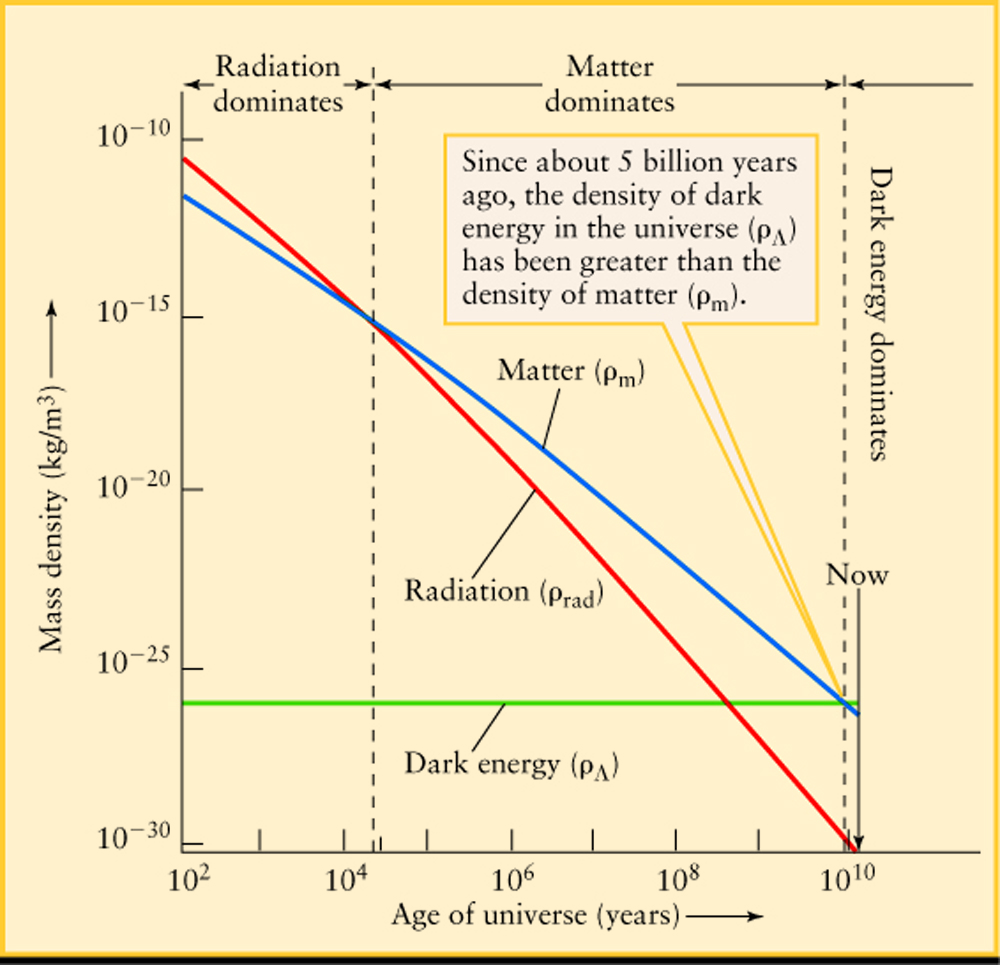
- How the expansion changes depends on the matter content of the
Universe, and what type of matter dominates. Einstein equations give us
the deceleration parameter
q = &Omegarad + 1/2 &Omegam - &Omega&Lambda
when q > 0 expansion decelerates, while it accelerates if q < 0
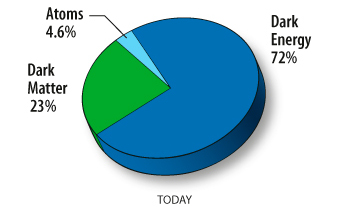
- Neglecting &Omegarad, we conclude that
Universe was decelerating while &Omegam > 2 &Omega&Lambda and accelerating afterwards.
Note, in this formula we consider all &Omega's as functions of time, not just
the values at the present moment. For example
&Omegam=&rhom(t)/&rhocrit(t), etc.
You can see that to find whether Universe accelerates or not at a particular
redshift, one does not need to know how critical density changes with time.
- Note that ordinary matter always causes deceleration. One need an
unusual type of energy which density does not decrease with expansion
to have acceleration ! This is very strong argument for existenceof
"dark energy"
|
|