Lecture 30: The Expanding Universe

Balloon example

• Surface of the baloon represents two-dimensional (2D) space (balloon itself is three-dimensional (3D) object)
• Our Universe may have been 3D surface of 4D baloon
• Say, in this 2D space live flat 2D galaxies
• Expansion of the Universe is similar to the stretching of the balloon surface
• Its area increases (volume for us), the distances between every pairs of galaxies increases.
• We speak about "space expansion" but object that kept together by forces, are not stretched. Galaxies are not stretched, they kept to the same size by gravity. So do groups and clusters of galaxies, but larger structures are being stretched.

Cosmological redshift

• Proper interpretation of the redshift of light from distant galaxies is not Doppler effect, but stretching of the photons as they propagate through the space.
• As Universe expands, local velocity of photons is always c
• Local velocity of galaxies never exceeds c either. Even for distant ones, distance to which is increasing faster than c ! Actually, if only expansion is present, galaxies are at rest relative to the local space.
• This is because the position of distance galaxy at exactly the same moment as observation is unobservable in any experiments.

Galaxy c

• Define d_c distance between galaxies c and d at t₂.
• Define v_c relative velocity between galaxies c and d.
• At time t₂, d_c = 2 m (to the left of d)
• The relative velocity of galaxy c with respect to galaxy d is:
  
  v_c = (change in distance)/(change in time)
  = (2m - 1m)/1s
  = (1m)/(1s) (moving to the left)
  
  
• (At time t₁ the galaxies are separated by 1m and at t₂ they are separated by 2m, so the change in distance is 1m over a time period of 1s.)

Galaxy e

• A similar calculation shows that galaxy e (to the right of d) has:
• d_e = 2 m
• v_e = + 1m/s

Galaxy b

• At t₂, the displacement and velocity relative to d for galaxy b are:
• d_b = 4 m (to the left)
• v_b = (4m - 2m)/1s = 2 m/s (to the left)

Galaxy f

• At t₂, the displacement and velocity relative to d for galaxy f are:
• d_f = 4 m (to the right)
• v_f = (4m - 2m)/1s = 2 m/s (to the right)

Galaxy a

• At t₂, the displacement and velocity relative to d for galaxy a are:
• d_a = 6 m (to the left)
• v_a = (6m - 3m)/1s = 3 m/s (to the left)

Galaxy g

• At t₂, the displacement and velocity relative to d for galaxy g are:
• d_g = 6 m (to the right)
• v_g = (6m - 3m)/1s = 3 m/s (to the right)

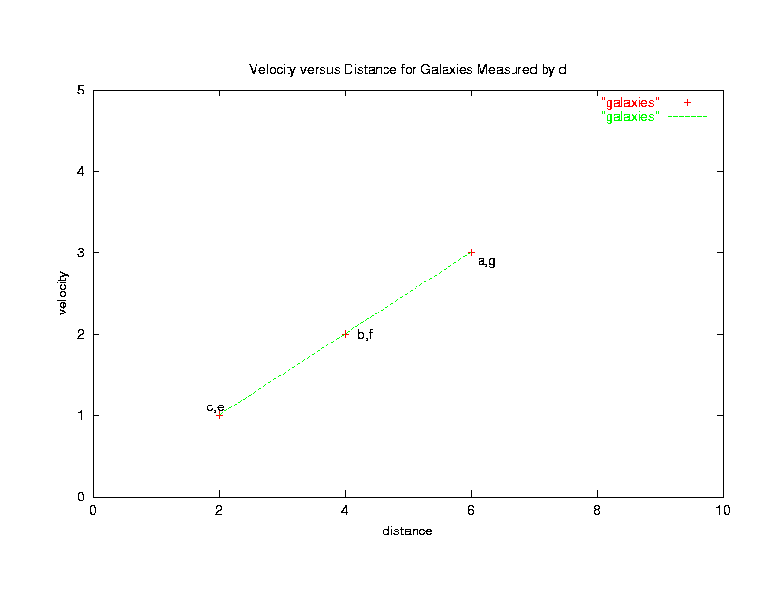
• The astronomer in galaxy d observes that all galaxies are moving away from galaxy d and that the velocity increases linearly with distance.

• Another astronomer in another galaxy (say galaxy c ) can also make similar measurements.

• The astronomer at galaxy c will also find that all galaxies are moving away from galaxy c and that the slope of the graph of velocity versus distance is 0.5/s, exactly the same as for the astronomer in galaxy d .

• However, one important difference: This model has two galaxies to the left of galaxy c and four galaxies to the right of galaxy c.

• The astronomer in galaxy c will see that more galaxies are in one direction, and thus can tell that galaxy d is at a special location.

• If we wish to adopt the Copernican principle, that we are not in a special location in the universe, we should add another complication to this simple one-dimensional model. Two ways to change the model are:

1. The universe should be infinite in size, so that an infinite number of galaxies exist. This means that there is no edge to the universe and that every astronomer in every galaxy sees that there are an infinite number of galaxies to the right and to the left. This type of model is called open.
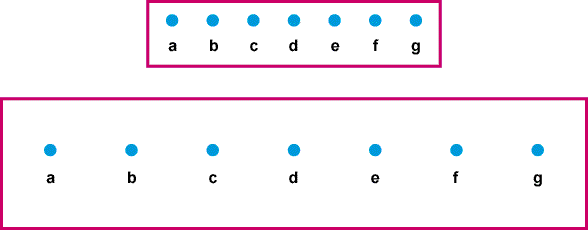
2. The universe has a finite number of galaxies, but they exist on a closed loop, so that galaxy a is next to galaxy g. In this universe it is possible to travel in one direction for and end up at the starting point. This type of model is called closed.

• Both open and closed models have the property that there is no special galaxy. All astronomers making cosmological measurements from different galaxies agree on the properties of the universe.
• Balloon example (in 3D) is exactly the closed model of the Universe.
• An infinite 3D plane is an example of an open model of the Universe (but there are others).

• We understood that cosmological redshift
  z = (&lambda₀-&lambda)/&lambda is the result of stretching the space during the lifetime of the photon.
• Thus, the redshift can be immediately related to how much the Universe has expanded between the photon emission and observation.
  
  Let us describe the expansion of the Universe with the help of scale factor a(t) which gives and average distance between galaxies. Then a(t₀)/a(t) gives the amount of expansion between time t and t_o.
  
  Then, this is the amount by which the wavelength of the photon was stretched, thus
  
  z = &lambda₀/&lambda -1 = a(t₀)/a(t) - 1
• We usually write
  
  1 + z = a(t₀)/a(t)
• Redshift is convenient way to measure time. Saying something happened at redshift z means when the Universe was compressed 1+z times, independently on how exactly the expansion was proceeding.
• At the present moment z=0, and z increases for more and more earlier times.