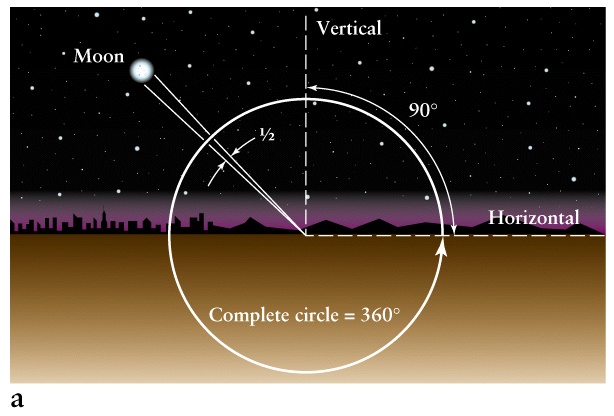
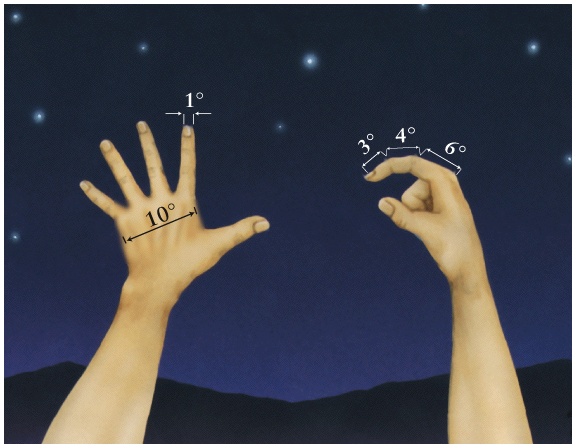
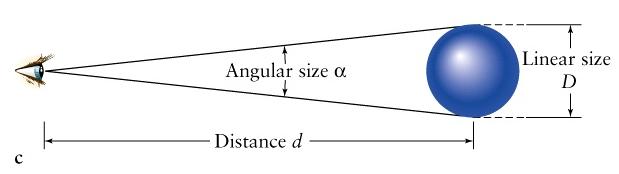
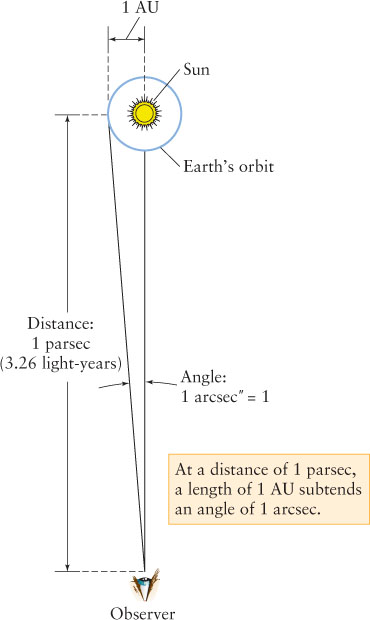
- Viewed from a distance of 1 parsec the radius of Earth orbit
, which is by definition 1AU, subtends the angle of 1 '',
- 1 parsec = 1 pc = 3.26 ly
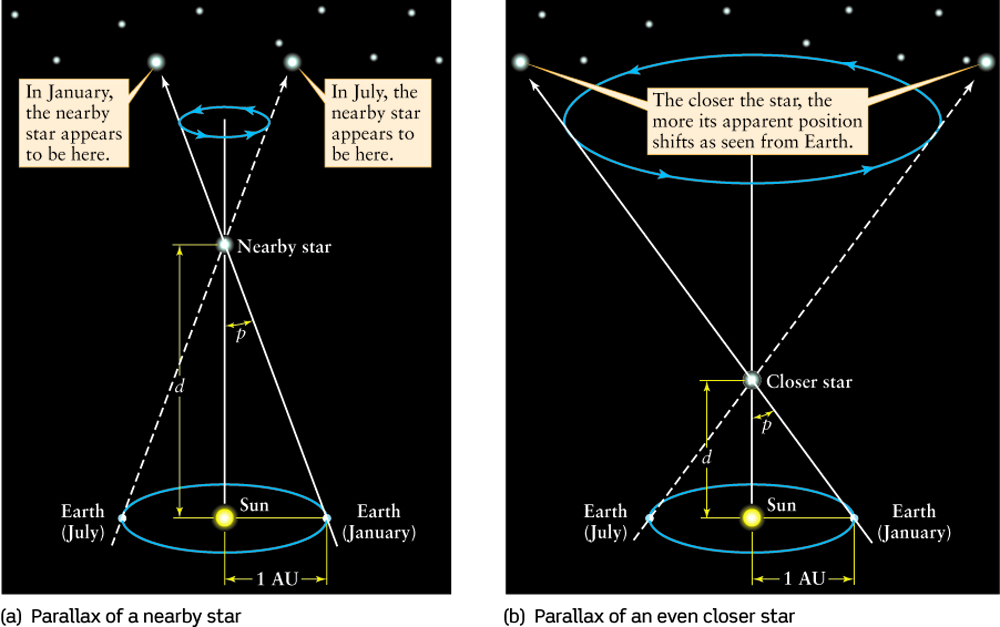
- But why ??? Really parsec appears a natural unit when one
considers effect of parallax as an observer
on the Earth moves around the Sun
- When is it convenient to measure distances in parsecs ?
Parallaxes of nearby stars are typically fraction of arcseconds, that's why
a parsec is a natural unit to measure distances to them. The nearest star
(Alpha Centauri) has a parallax of 0.746 '' and the distance 1.34 pc
|
 |