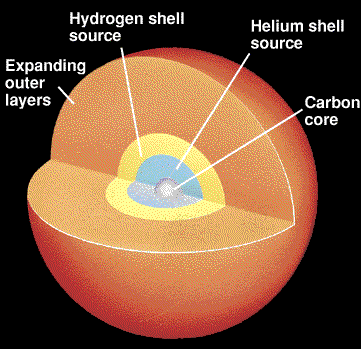
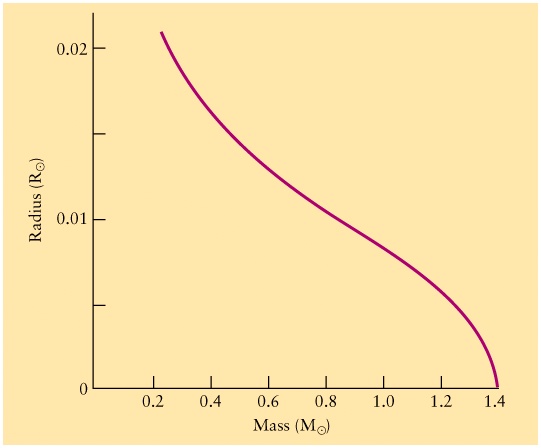
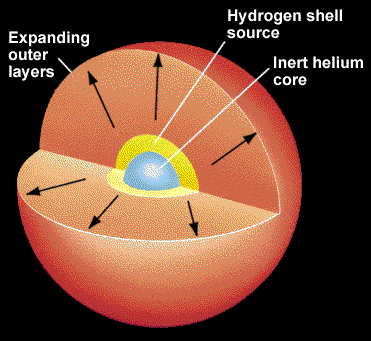
- As the contracting core heats up,
a shell of hydrogen around the inert Helium
core will heat up to 15 million K and begin to fuse.
- This begins the phase of shell-Hydrogen burning.
- The burning of Hydrogen in the shell actually produces more
energy than in the main sequence phase (due to the higher T).
- However, the inert Hydrogen outside of the shell hinders
the movement of the photons.
- When photons have trouble moving through a medium, they
end up pushing outwards on the matter. This is called
radiation pressure.
- The extra photons produced in the shell of hydrogen
push outwards on the outer layers of the star.
- The expansion of the outer layers causes them to cool
down.
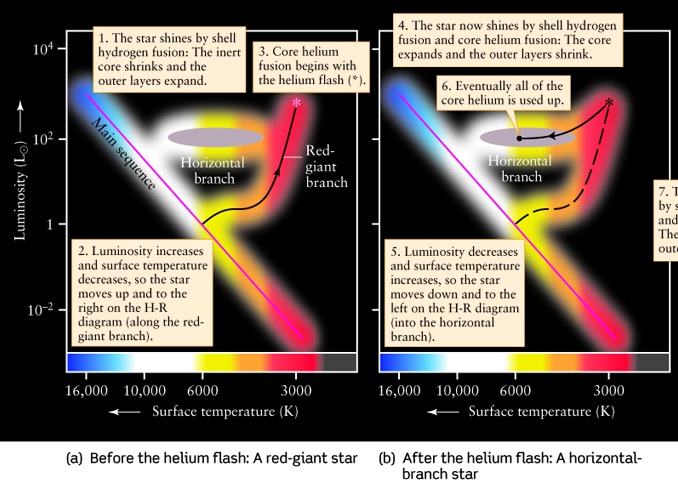
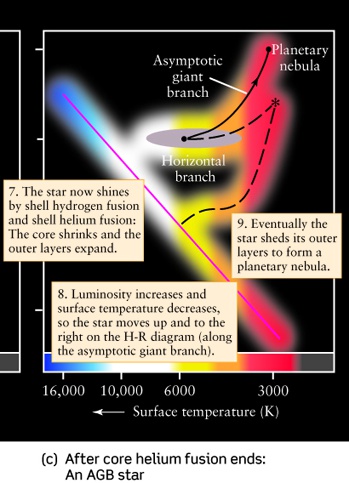
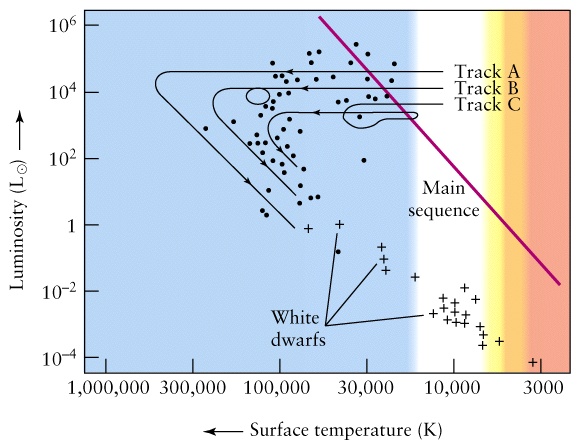
- General Picture in this phase:
- Helium core contracts and heats up.
- Hydrogen shell around the core contracts, heats up and ignites.
- Outer Hydrogen expands and cools off.
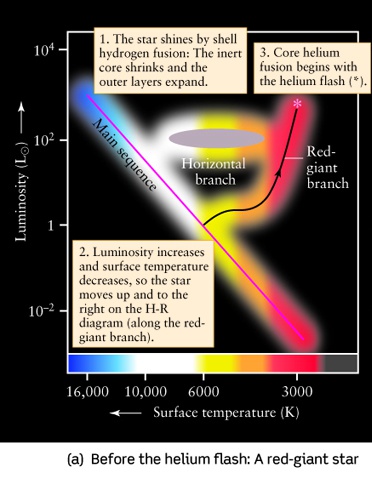
- Since the star's surface temperature is lower, it
will look redder than during the main sequence phase.
- The radius of the star increases by a large factor
and becomes a giant.
- Final radius is 10 to 100 times the original size of the star.
- Final surface temperature is about 1/2 the original surface temperature.
- Luminosity given by blackbody equation increases.
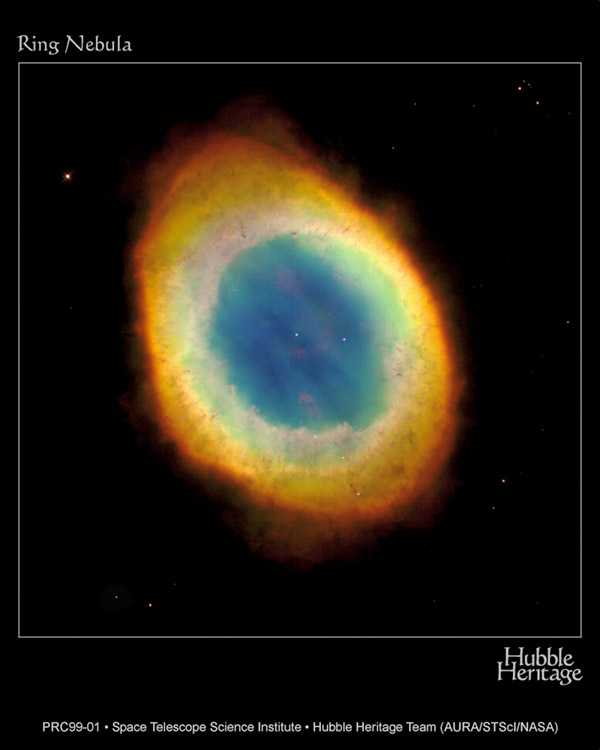
- This stage is called the Red Giant Stage of a star's life.
- This stage lasts for about 2 billion years for a Sun-like star.
|
 |