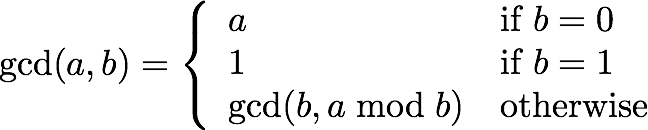
N = { 0, 1, 2, 3, 4, ... }and we will only ever see a small bit of them in our lifetime.
Z = { ... -3, -2, -1, 0, 1, 2, 3, ... }but won't tell you how to get them.
a, and for any positive natural number b (that is 0 < b), then there exist unique natural numbers q called the quotient and r called the remainder such that a = b * q + r and 0 <= r < bThe Division Algorithm is usually stated for integers as follows:
for all integers a
for all integers b such that b > 0
there exist unique integers q, r such that
a = b * q + r and 0 <= r < b div and mod that let you perform the division algorithm. They have the property that for all integers a
for all integers b such that b > 0
a = b * (a div b) + (a mod b) and 0 <= (a mod b) < b r is the remainder you would get from mod and the d is the result from div. For example: Let a = 25, b = 12
(a div b) = 25 div 12 = 2
(a mod b) = 25 mod 2 = 1
Therefore we can re-write 25 as:
a = b * (a div b) + (a mod b)
25 = 12 * (2) + (1)
Note: It gets a bit tricky to define the division algorithm when b < 0, and there a a few equally acceptable ways. If you write your program assuming one way, and the programmin language uses another way, you can be in for very unpleasant surprises that are very difficult to diagnose. a and b are integers, with at least one non-zero, then their greatest common divisor is the largest number that divides both a and b. It can be computed with the following recursive equation. and with Arduino program:
int32_t gcd(int32_t a, int32_t b) { |
if (b == 0) { |
return a; |
} |
if (b == 1) { |
return 1; |
} |
return gcd(b, a % b); |
} |
|
void setup() { |
Serial.begin(9600); |
Serial.println( gcd(36, 24) ); |
} |
|
void loop() { |
} |
n is a positive integer. Then arithmetic mod n is just normal integer arithmetic except that you are only allowed the operations of +, -, and * (multiplication), AND after every operation you take the result {mod n }. That is,a = b mod nif((a-b) mod n) = 0
a and b differ by a multiple of n. b is an inverse of a mod n if (a * b) mod n = 0. (a + (b * c) ) mod m = (a + ((b * c) mod m)) mod m
(a ** 3) mod m = ( (((a * a) mod m) * a) mod m)
((2 * 4) mod 3) = ( (2 mod 3) * (4 mod 3) ) mod 3
(8 mod 3) = ( (2) * (1) ) mod 3
2 = (2 mod 3) = 2
In general, for any op of the operations {+, -, * } we have that (a op b) mod n = ((a mod m) op (b mod m) ) mod m
(4 * 10) + 2where each of the decimal digits is from the set { 0, 1, 2, ..., 9 }. In base 10, each position goes up by a factor of 10 as you move from right to left. Numbering positions from right to left, starting with 0, the value of position
i is 2 ** i. For example 4096 = (4 * 10**3) + (0 * 10**2) + (9 * 10**1) + (6 * 10**0) n digits of our decimal number are d[n-1] d[n-2] d[n-3] ... d[2] d[1] d[0]
then the number they represent in decimal (base 10) is (d[n-1] * 10**(n-1)) + (d[n-2] * 10**(n-2)) + (d[n-3] * 10**(n-3)) +
... + (d[2] * 10**2) + (d[1] * 10**1) + (d[0] * 10**0)
But there is nothing special about our choice of digits. We could choose any base we like (provided it is bigger than 1). In binary, the base is 2, so we have the digits { 0, 1 }, and positions are powers of 2. These digits are commonly called bits (1 * 2**3) + (1 * 2**2) + (0 * 2**1) + (1 * 2**0)
= (8) + (4) + (0) + (1)
= 13
01101
+
00101
=
10010 00101
-
00011
=
00010
So this example is1101
+
0101
=
0010(without the final carry. Otherwise it would be10010.)
13 + 5 = 2. This may seem strange, but in fact it is just modular arithmetic, where the modulus is (2**n), which is the maximum number of bits we can use to represent our numbers, 4. (2 ** 4) = 16
That is, (13 + 5) mod 16 = 2 n=4 in the example above, 1101 + 0101 = 0010
x + 5 = 2
where 1101, x, must be -3. We can interpret n-bit binary numbers either as modular, or as signed. The underlying arithmetic does not change. Since the mod-n negative of a number x is (n-x), we can think of the numbers in the range 0, 1, ..., (2**(n-1) - 1)(2**n)-1, ...., 2**n-1, -2, -3, ..., -(2**n)-(2**n), -(2**n) + 1, ..., -1, 0, 1, ,..., 2**(n-1)-1| binary | decimal equivalent unsigned |
decimal equivalent signed |
| 0000 | 0 | 0 |
| 0001 | 1 | 1 |
| 0010 | 2 | 2 |
| 0011 | 3 | 3 |
| 0100 | 4 | 4 |
| 0101 | 5 | 5 |
| 0110 | 6 | 6 |
| 0111 | 7 | 7 |
| 1000 | 8 | -8 |
| 1001 | 9 | -7 |
| 1010 | 10 | -6 |
| 1011 | 11 | -5 |
| 1100 | 12 | -4 |
| 1101 | 13 | -3 |
| 1110 | 14 | -2 |
| 1111 | 15 | -1 |
Converting back follows the same steps:
0011, 3 in binary.
1100, bits flipped.
1101, added 1.
1101, -3.
0010, bits flipped.
0011, added 1.
| binary | hex digit |
equivalent decimal number |
| 0000 | 0 | 0 |
| 0001 | 1 | 1 |
| 0010 | 2 | 2 |
| 0011 | 3 | 3 |
| 0100 | 4 | 4 |
| 0101 | 5 | 5 |
| 0110 | 6 | 6 |
| 0111 | 7 | 7 |
| 1000 | 8 | 8 |
| 1001 | 9 | 9 |
| 1010 | a | 10 |
| 1011 | b | 11 |
| 1100 | c | 12 |
| 1101 | d | 13 |
| 1110 | e | 14 |
| 1111 | f | 15 |
1101 0101 is
| 1101 | 0101 |
| d | 5 |
d5 in hex. To make it clear that a number is in hex, it is usually writen with a prefix of 0x just like 0xd5. B you want, so long as B > 1. The digits in the representation have to come from { 0, 1, 2, ..., B-1 }Note for the digits bigger than 9 you need to introduce some symbols like we did for hex.
i is B ** i. And in general, if the n digits of our base-B number are d[n-1] d[n-2] d[n-3] ... d[2] d[1] d[0]
then the number they represent in base-B is (d[n-1] * B**(n-1)) + (d[n-2] * B**(n-2)) + (d[n-3] * B**(n-3)) +
... + (d[2] * B**2) + (d[1] * B**1) + (d[0] * B**0)
Note that a base-B representation looks very much like a polynomial. To convert a base-B number you can use a shortcut for evaluating polynomials called Horner's rule. For example, in base 3, the number 1201 is ((( (1 * 3) + 2 ) * 3 + 0 ) * 3 + 1) = 46So when we mod with the base B, all higher powers of B vanish, and we are left with the rightmost digit. So for any non-negative integer(B ** n) mod B = 0ifn > 0
x, the rightmost digit in Base-B is x mod B. 217 mod 10 is 7. In binary (Base 2), 217 mod 2 is 1, which is consistent with the binary representation 1101 1001 for 217. Note in hex, 217 is 0xd9. 217 mod 16 = 9 ((x * B**n) div B) = (x * B**(n-1))
That is, dividing by the Base B shifts the entire number over one position. (217 div 10) is 21. In binary (Base 2), (217 div 2) is 108, which is consistent with shifting the binary representation 1101 1001 over one position, to get 0110 1100 for 108. Note in hex, 217 is 0xd9 217 div 16 = 13 = 0xd void setup() |
{ |
Serial.begin(9600); |
|
// prints title with ending line break |
Serial.println("Base Conversion Example"); |
} |
|
uint16_t x = 217; |
uint16_t base = 2; |
|
void loop() |
{ |
uint16_t y; |
uint16_t digit; |
|
Serial.print("Converting "); |
Serial.print(x, DEC); |
Serial.print(" into base "); |
Serial.print(base, DEC); |
Serial.println(" with reversed digits!"); |
|
y = x; |
while (y > 0) { |
// extract out rightmost base digit |
digit = y % base; |
y = y / base; |
Serial.print(digit); |
} |
Serial.println(""); |
|
delay(1000); |
|
|
} |
|
void setup() |
{ |
Serial.begin(9600); |
|
// prints title with ending line break |
Serial.println("Base Conversion Example"); |
} |
|
uint16_t x; |
uint8_t base = 2; |
|
// where we will place the digits of x |
int16_t Digits[32]; |
int16_t num_digits; |
|
void loop() |
{ |
uint16_t y; |
uint16_t digit; |
uint16_t dig_pos; |
|
x = -1; |
|
Serial.print("Converting "); |
Serial.print(x, DEC); |
Serial.print(" into base "); |
Serial.print(base, DEC); |
Serial.println(""); |
|
y = x; |
dig_pos = 0; |
num_digits = 0; |
while (y > 0) { |
// extract out rightmost base B digit |
digit = y % base; |
y = y / base; |
// and put it into digit position dig_pos |
Digits[dig_pos] = digit; |
dig_pos++; // next position |
num_digits++; // count this digit |
} |
|
// now print out the digits left to right |
for (dig_pos = num_digits-1; dig_pos--; dig_pos >=0) { |
Serial.print(Digits[dig_pos], DEC); |
Serial.print(" "); |
} |
Serial.println(""); |
|
delay(1000); |
} |
|
| 3. Bits, Bytes, and Modular Artithmetic Tangible Computing / Version 3.20 2013-03-25 |