Functional Programming - 13. Haskell Examples

Functional Programming

13. Haskell Examples - Simple Parsing

13.1 Building up a simple parser for numbers

code/Haskell/Parse/parse-number-0.hs

import Data.Char

-- A simple parse of a list of tokens, each token a digit char,

-- to produce an integer.

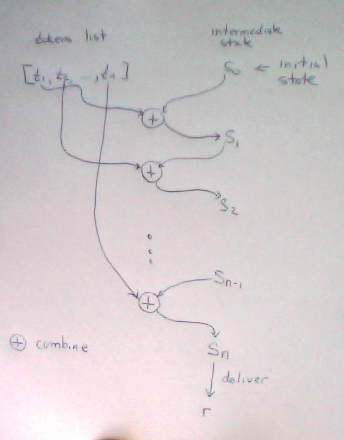
-- a typical parse scans the tokens and accumulates the intermediate

-- results of the parse. So the recursive form takes a pair

-- ( tokens, results ) -> ( tokens', results')

-- where the parse step consumes some tokens and computes new results.

-- In general, the idea is to take the current state of the parse

-- in (tokens, results), remove the first token to get tokens', and then

-- process that token in the context of the current results and product a

-- new set results'

tokenToDigit :: Char -> Int

tokenToDigit c

| c == '0' = 0

| c == '1' = 1

| c == '2' = 2

| c == '3' = 3

| c == '4' = 4

| c == '5' = 5

| c == '6' = 6

| c == '7' = 7

| c == '8' = 8

| c == '9' = 9

parseNumber1_r :: ( [ Char ], Int ) -> ( [ Char ], Int)

parseNumber1_r ( [], result ) = ( [], result )

parseNumber1_r ( (token:tokens), result ) =

parseNumber1_r ( tokens, result * 10 + (tokenToDigit token) )

parseNumber1 :: [ Char ] -> Int

parseNumber1 s = snd ( parseNumber1_r ( s, 0) )

-- Now let's generalize the parser to take a function combine that is

-- used to combine the current token with the previous result to produce

-- the new result. We handle the fetching of the next token etc. in the

-- recursor.

parseNumber2_r :: (Char -> Int -> Int) -> ( [ Char ], Int ) -> ([ Char ], Int)

parseNumber2_r combine ( [], result ) = ( [], result )

parseNumber2_r combine ( (token:tokens), result ) =

(parseNumber2_r combine ( tokens, ( combine token result) ) )

parseNumber2 :: [ Char ] -> Int

parseNumber2 s = snd ( parseNumber2_r

-- the combin function does the same as above

(\ token result -> result * 10 + (tokenToDigit token))

( s, 0) )

-- Let's express this same code, but using type synonyms to make the

-- function signatures clearer

type Token = Char

type Result = Int

-- Also, instead of doing the parse immediately, return a parser function

-- that takes a list of tokens and returns a result

parseLang1 :: (Token -> Result -> Result) -> Result ->

( [ Token ] -> Result )

parseLang1 combine init_result = \ tokens ->

snd ( parseLang1_r combine ( tokens, init_result ) )

parseLang1_r :: (Token -> Result -> Result) ->

( [ Token ], Result ) -> ([ Token ], Result)

parseLang1_r combine ( [], result ) = ( [], result )

parseLang1_r combine ( (token:tokens), result ) =

(parseLang1_r combine ( tokens, ( combine token result) ) )

parseNumber3 = parseLang1

(\ token result -> result * 10 + (tokenToDigit token)) 0

-- In general, Result is not going to be sufficient for keeping track

-- of the intermediate parse information. So we introduce

-- an Intermediate type which used during the parse, and a function

-- deliver :: Intermediate -> Result

-- that extracts the final result from the intermediate data of the parse

-- Our parse state is now of type ( [ Tokens ] , Intermediate )

type Intermediate = Int

-- again, return a parser

parseLang2 :: (Token -> Intermediate -> Intermediate) -> Intermediate ->

(Intermediate -> Result ) ->

( [ Token ] -> Result )

parseLang2 combine init_intermediate deliver = \ tokens ->

deliver (snd ( parseLang2_r combine ( tokens, init_intermediate ) ) )

parseLang2_r :: (Token -> Intermediate -> Intermediate) ->

( [ Token ], Intermediate ) -> ([ Token ], Intermediate)

parseLang2_r combine ( [], intermediate ) = ( [], intermediate )

parseLang2_r combine ( (token:tokens), intermediate ) =

(parseLang2_r combine ( tokens, ( combine token intermediate ) ) )

-- and our final act is to generate a parser for numbers. Note how the

-- deliver function is just the identitiy in this case.

parseNumber4 = parseLang2

(\ token intermediate -> intermediate * 10 + (tokenToDigit token))

0

(\ intermediate -> intermediate )

-- Next, we want to allow negative numbers.

13.2 Making the parsing process abstract

code/Haskell/Parse/parse-number-1.hs

import Data.Char

-- A generic look-ahead-1 token parser

parseGen :: (Token -> Intermediate -> Intermediate) -> Intermediate ->

(Intermediate -> Result ) -> ( [ Token ] -> Result )

parseGen combine init_intermediate deliver = \ tokens ->

deliver (snd ( parseGen_r combine ( tokens, init_intermediate ) ) )

parseGen_r :: (Token -> Intermediate -> Intermediate) ->

( [ Token ], Intermediate ) -> ([ Token ], Intermediate)

parseGen_r combine ( [], intermediate ) = ( [], intermediate )

parseGen_r combine ( (token:tokens), intermediate ) =

(parseGen_r combine ( tokens, ( combine token intermediate ) ) )

-- now build a parser that understands negative numbers

type Token = Char

type Result = Int

type Intermediate = (Char, Int)

-- The intermediate state of the parse is represented by a pair. The first

-- element is a Char:

-- ' ' meaning that no digit has been seen yet

-- '-' meaning that a - sign was encountered before the first digit

-- '+' meaning that a + sign was encountered before the first digit, or

-- that no sign at all was encountered.

-- Note, we can use Char.isDigit c to test is c is a digit

tokenToDigit :: Token -> Int

tokenToDigit c

| c == '0' = 0

| c == '1' = 1

| c == '2' = 2

| c == '3' = 3

| c == '4' = 4

| c == '5' = 5

| c == '6' = 6

| c == '7' = 7

| c == '8' = 8

| c == '9' = 9

combine' :: (Token -> Intermediate -> Intermediate)

combine' token (sign, value )

-- handle the leading sign, if any

| sign == ' ' && token == '-' = ('-', value)

| sign == ' ' && token == '+' = ('+', value)

| sign == ' ' = ('+', tokenToDigit token)

| otherwise = (sign , value * 10 + (tokenToDigit token))

deliver' :: (Intermediate -> Result )

deliver' (sign, value )

| sign == '-' = (0 - value)

| otherwise = value

parseNumber = parseGen combine' (' ', 0) deliver'

13.3 Evaluation as parsing

code/Haskell/Parse/eval-arith-expr.hs

import Data.Char

-- A generic look-ahead-1 parser

parseGen :: (Token -> Intermediate -> Intermediate) -> Intermediate ->

(Intermediate -> Result ) -> ( [ Token ] -> Result )

parseGen combine init_intermediate deliver = \ tokens ->

deliver (snd ( parseGen_r combine ( tokens, init_intermediate ) ) )

parseGen_r :: (Token -> Intermediate -> Intermediate) ->

( [ Token ], Intermediate ) -> ([ Token ], Intermediate)

parseGen_r combine ( [], intermediate ) = ( [], intermediate )

parseGen_r combine ( (token:tokens), intermediate ) =

(parseGen_r combine ( tokens, ( combine token intermediate ) ) )

-- now build a parser that evaluates postfix + * arithmetic expressions

type Token = String

type Result = Int

type Intermediate = [ Int ]

combine' :: (Token -> Intermediate -> Intermediate)

combine' "+" (x:y:stack) = (y+x) : stack

combine' "*" (x:y:stack) = (y*x) : stack

combine' token stack = (read token::Int) : stack

deliver' :: (Intermediate -> Result )

deliver' (top:rest) = top

-- if you wanted to return the string representation, you could do this

-- type Result = String

-- deliver' (top:rest) = show top

evalArith = parseGen combine' [] deliver'

code/Haskell/Parse/eval-bool-expr.hs

import Data.Char

parseGen :: (Token -> Intermediate -> Intermediate) -> Intermediate ->

(Intermediate -> Result ) -> ( [ Token ] -> Result )

parseGen combine init_intermediate deliver = \ tokens ->

deliver (snd ( parseGen_r combine ( tokens, init_intermediate ) ) )

parseGen_r :: (Token -> Intermediate -> Intermediate) ->

( [ Token ], Intermediate ) -> ([ Token ], Intermediate)

parseGen_r combine ( [], intermediate ) = ( [], intermediate )

parseGen_r combine ( (token:tokens), intermediate ) =

(parseGen_r combine ( tokens, ( combine token intermediate ) ) )

-- now build a Boolean formula evaluator

type Token = Char

type Result = String

type Intermediate = [ Bool ]

combine' :: (Token -> Intermediate -> Intermediate)

combine' ' ' stack = stack

combine' '0' stack = False:stack

combine' '1' stack = True:stack

combine' '+' (x:y:stack) = (x || y):stack

combine' '*' (x:y:stack) = (x && y):stack

deliver' :: (Intermediate -> Result )

deliver' (top:stack)

| top = "1"

| otherwise = "0"

evalBool = parseGen combine' [] deliver'

-- evalBool ( (evalBool "1 0 +") ++ (evalBool "1 1 *") ++ "+" )

We can move the parseGen_r helper function into the definition of parseGen, thus making it local, and at the same time eliminate the passing of the combine function. code/Haskell/Parse/eval-arith-expr-1.hs

import Data.Char

-- A generic look-ahead-1 parser

parseGen :: (Token -> Intermediate -> Intermediate) -> Intermediate ->

(Intermediate -> Result ) -> ( [ Token ] -> Result )

parseGen combine init_intermediate deliver = \ tokens ->

deliver (snd ( parseGen_r ( tokens, init_intermediate ) ) )

where

parseGen_r :: ( [ Token ], Intermediate ) -> ([ Token ], Intermediate)

parseGen_r ( [], intermediate ) = ( [], intermediate )

parseGen_r ( (token:tokens), intermediate ) =

(parseGen_r ( tokens, ( combine token intermediate ) ) )

-- now build a parser that evaluates postfix + * arithmetic expressions

type Token = String

type Result = Int

type Intermediate = [ Int ]

combine' :: (Token -> Intermediate -> Intermediate)

combine' "+" (x:y:stack) = (y+x) : stack

combine' "*" (x:y:stack) = (y*x) : stack

combine' token stack = (read token::Int) : stack

deliver' :: (Intermediate -> Result )

deliver' (top:rest) = top

-- if you wanted to return the string representation, you could do this

-- type Result = String

-- deliver' (top:rest) = show top

evalArith = parseGen combine' [] deliver'

Now look at how the data flows through the parsing process. At each step, a token is consumed by combining with the current intermediate parse state, and a new intermediate parse state is produced.

This looks exactly like a foldl, except that we need to swap the order of the arguments to combine. code/Haskell/Parse/eval-arith-expr-2.hs

import Data.Char

-- A generic look-ahead-1 parser

parseGen :: (Token -> Intermediate -> Intermediate) -> Intermediate ->

(Intermediate -> Result ) -> ( [ Token ] -> Result )

parseGen combine init_intermediate deliver = \ tokens ->

(deliver (foldl (\ i t -> combine t i) init_intermediate tokens ))

-- now build a parser that evaluates postfix + * arithmetic expressions

type Token = String

type Result = Int

type Intermediate = [ Int ]

combine' :: (Token -> Intermediate -> Intermediate)

combine' "+" (x:y:stack) = (y+x) : stack

combine' "*" (x:y:stack) = (y*x) : stack

combine' token stack = (read token::Int) : stack

deliver' :: (Intermediate -> Result )

deliver' (top:rest) = top

-- if you wanted to return the string representation, you could do this

-- type Result = String

-- deliver' (top:rest) = show top

evalArith = parseGen combine' [] deliver'

So we might as well redefine the signature of combine to make it match foldl, and we get the following: code/Haskell/Parse/eval-arith-expr-3.hs

import Data.Char

-- A generic look-ahead-1 parser

-- Modified from previous example to swap order of arguments to

-- combine so that its type matches that required by foldl

parseGen :: (Intermediate -> Token -> Intermediate) -> Intermediate ->

(Intermediate -> Result ) -> ( [ Token ] -> Result )

parseGen combine init_intermediate deliver = \ tokens ->

(deliver (foldl combine init_intermediate tokens ))

-- now build a parser that evaluates postfix + * arithmetic expressions

type Token = String

type Result = Int

type Intermediate = [ Int ]

combine' :: (Intermediate -> Token -> Intermediate)

combine' (x:y:stack) "+" = (y + x) : stack

combine' (x:y:stack) "*" = (y * x) : stack

combine' stack token = (read token::Int) : stack

deliver' :: (Intermediate -> Result )

deliver' [top] = top

evalArith = parseGen combine' [] deliver'

calc = evalArith . words

13.5 Typeclasses and Handling Errors

The parser so far is optimistic - if the expression evaluates we are fine. But there could be errors. We will use type classes to create a new type that either contains an OK value, or contains an ERROR.

Here is a partial implementation of the postfix calculator that deals with errors (the full version is the next assignmemnt). code/Haskell/Parse/eval-arith-class-1.hs

import Data.Char

-- Check out http://learnyouahaskell.com/making-our-own-types-and-typeclasses

-- A generic look-ahead-1 parser

-- Modified from previous example to swap order of arguments to

-- combine so that its type matches that required by foldl

parseGen :: (Intermediate -> Token -> Intermediate) -> Intermediate ->

(Intermediate -> Result ) -> ( [ Token ] -> Result )

parseGen combine init_intermediate deliver = \ tokens ->

(deliver (foldl combine init_intermediate tokens ))

-- now build a parser that evaluates postfix + * arithmetic expressions

-- encapsulate a value of type e or an error message

-- a Value can be a number or an error

data Value e = OK e | Error String deriving Eq

-- assuming we know how type e can be shown, i.e. Show e, then

-- we know how to show a Value e type

instance (Show e) => Show (Value e) where

show (OK x) = (show x)

show (Error s) = "ERROR: " ++ s

type Token = String

type Result = Value Int

type Intermediate = [ (Value Int) ]

-- an algebra is a things that knows about plus and times

class Algebra a where

plus :: a -> a -> a

times :: a -> a -> a

-- assuming that we know how to + and * things of type e, (i.e.

-- we have Num e, then we have algrbra's over Value e

instance (Num e) => Algebra (Value e) where

plus (OK x) (OK y) = (OK (x+y))

times (OK x) (OK y) = (OK (x*y))

-- ? need to handle ERROR also

-- Now we have a calculator that works on type Value

combine' :: (Intermediate -> Token -> Intermediate)

combine' (x:y:stack) "+" = (plus y x) : stack

combine' (x:y:stack) "*" = (times y x) : stack

combine' stack token = (OK (read token::Int)) : stack

deliver' :: (Intermediate -> Result )

deliver' [] = Error "No result on stack"

deliver' [top] = top

deliver' ((Error top):rest) = Error top

-- ? what else

evalArith = parseGen combine' [] deliver'

calc = evalArith . words

And here is the version we did in class that handles a larger number of errors, and uses the reads function to handle conversion to integers in a way that copes with non-integers. code/Haskell/Parse/calculator.hs

import Data.Char

-- Check out http://learnyouahaskell.com/making-our-own-types-and-typeclasses

-- parsGen ::

-- (intermediate -> token -> intermediate) -> intermediate ->

-- (intermediate -> result ) -> ( [ token ] -> result )

parseGen combine init_intermediate deliver = \ tokens ->

(deliver (foldl combine init_intermediate tokens ))

-- now build a parser that evaluates postfix + * arithmetic expressions

-- type constuctors take types and produce new types

-- encapsulate a value of type e or an error message

-- a Value can be a number or an error

-- Value is a type constructor, OK and Error are value constructors

data Value e = OK e | Error String deriving Eq

-- assuming we know how type e can be shown, i.e. Show e, then

-- we know how to show a Value e type, so Value e is then an instance

-- of the Show typeclass. Think of a typeclass as an interface

instance (Show e) => Show (Value e) where

show (OK x) = (show x)

show (Error s) = "ERROR: " ++ s

-- the typeclass Algebra

-- an algebra is a things that knows about plus and times

class Algebra a where

plus :: a -> a -> a

times :: a -> a -> a

divide :: a -> a -> a

-- assuming that we know how to + and * things of type e, (i.e.

-- we have Num e, then we have algebra's over Value e

{-

instance (Num e) => Algebra (Value e) where

plus (OK x) (OK y) = (OK (x+y))

plus (Error s) _ = (Error s)

plus _ (Error s) = (Error s)

times (OK x) (OK y) = (OK (x*y))

times (Error s) _ = (Error s)

times _ (Error s) = (Error s)

divide _ _ = (Error "No divide operation")

-}

-- if we want to introduce division, we need the Integral typeclass

-- which then means we get the Num properties also.

instance (Num e, Integral e) => Algebra (Value e) where

plus (OK x) (OK y) = (OK (x+y))

plus (Error s) _ = (Error s)

plus _ (Error s) = (Error s)

times (OK x) (OK y) = (OK (x*y))

times (Error s) _ = (Error s)

times _ (Error s) = (Error s)

divide (OK x) (OK y)

| y == 0 = (Error "divide by zero")

| True = (OK (quot x y))

divide (Error s) _ = (Error s)

divide _ (Error s) = (Error s)

-- to get the instances of Algebra in ghci try :info Algebra

-- to get the kind of type constructor Value in ghci try :k Value

-- type Token = String

-- type Result = Value Int

-- type Intermediate = [ (Value Int) ]

parseNum t = case reads t :: [(Int, String)] of

[(x, "")] -> (OK x)

_ -> (Error ("not a Number " ++ t))

applyOp "+" y x = (plus y x)

applyOp "*" y x = (times y x)

applyOp "/" y x = (divide y x)

applyOp token _ _ = (Error ("Not an operator: " ++ token) )

-- Now we have a calculator that works on type Value

-- combine' :: (Intermediate -> Token -> Intermediate)

combine' stack token = case (parseNum token) of

(OK x) -> (OK x) : stack

(Error _) -> case stack of

(x:y:rest) -> (applyOp token y x) : rest

_ -> [ (Error ("Insufficient arguments on stack for " ++ token) ) ]

-- deliver' :: (Intermediate -> Result )

deliver' [] = Error "No result on stack"

deliver' [top] = top

deliver' ((Error top):rest) = Error top

deliver' (top:stack) = Error "Too many results on stack"

evalArith = parseGen combine' [] deliver'

calc = evalArith . words

13. Haskell Examples - Simple Parsing
Notes on Functional Programming / Version 2.10 2014-02-24

13.1 Building up a simple parser for numbers

13.2 Making the parsing process abstract

13.3 Evaluation as parsing

13.4 Cleaning Up the Parser

13.5 Typeclasses and Handling Errors