#lang racket |
|
; all functions can be written in continuation passing style in which |
; the next thing to be done is passed into the call along with the |
; arguments. The next thing to be done, cc, is called a continuation. |
; Programming in this way is called continuation passing style (CPS). |
|
(define C+ (lambda (x y cc) (cc (+ x y)))) |
(define C* (lambda (x y cc) (cc (* x y)))) |
|
(C+ 3 5 (lambda (r) r)) ; return result 3 + 5 |
; same as ((lambda (r) r) (+ 3 5)) |
|
; to chain a sequence of cps functions computing (3 + 5) * 10 |
(C+ 3 5 (lambda (r) |
(C* r 10 (lambda (rr) rr)))) |
|
; this is the same as |
|
|
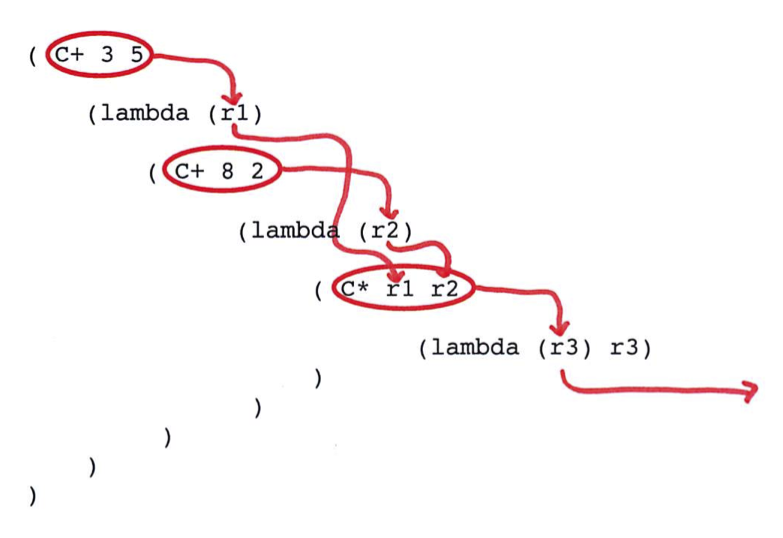
; and even for this: (3 + 5) * (8 + 2) i.e. (* (+ 3 5) (+ 8 2) ) |
; Note how it reads left to right. |
(C+ 3 5 |
(lambda (r1) ( C+ 8 2 |
(lambda (r2) (C* r1 r2 (lambda (r3) r3) ) |
) |
) |
) |
) |
|
; this means that we can even write recursive functions that make |
; multiple recursive calls in continuation passing style. The |
; stack is replaced by bindings in lambdas to heap values |
#lang racket |
|
; Converting a simple recursive function into tail recursive form using |
; continuation passing style of computation. |
|
; In general, a simple recursive function can be written this way as a |
; combinator of functions that say how to break the problem into smaller |
; pieces. For example, this defines factorial recursively: |
|
(define AtBase? (lambda (x) (<= x 1))) |
(define BaseCase (lambda (x) 1)) |
(define Combine (lambda (x recursion-result) (* x recursion-result))) |
(define Decomp (lambda (x) (- x 1))) |
|
(define fn (lambda (x) |
(if (AtBase? x) (BaseCase x) |
(Combine x (fn (Decomp x))) |
))) |
|
; note that this is not tail recursive. The inner recursive call |
; (fn (Decomp x)) |
; is used to combine the result with the data available at the call |
; That is, there is work to do after the recursion completes. |
|
; Let's rewrite the function so that we not only do the recursive |
; call, but also pass along the work to do on the result of the call. |
; That is, we pass on the continuation of work to be done. |
|
(define fn-cc-r (lambda (x cc) |
(if (AtBase? x) |
; compute the base case, and then continue |
(cc (BaseCase x)) |
; recurse, and then combine the result, and continue. Note |
; this is tail recursive in fn-cc-r |
(fn-cc-r (Decomp x) (lambda (result) (cc (Combine x result)))) |
) |
)) |
|
(define fn-cc (lambda (x) |
(fn-cc-r x (lambda (result) (begin (print "Hello") (print result)))))) |
|
(fn 3) |
(fn-cc 3) |
|
#lang racket |
|
; Combinators for generic generation of recursive functions over linear |
; data structure, using direct and continuation passing style of computation. |
|
; In general, a simple recursive function can be written as a |
; combinator on functions that say how to break the problem into smaller |
; pieces, and then combine them into a bigger result. |
|
; For example, this defines factorial recursively: |
|
(define AtBase? (lambda (x) (<= x 1))) |
(define BaseCase (lambda (x) 1)) |
(define Combine (lambda (x recursion-result) (* x recursion-result))) |
(define Decomp (lambda (x) (- x 1))) |
|
; Direct style |
|
(define (gen-fn-lin AtBase? BaseCase Combine Decomp) |
; we need the lerrec here because we want to refer to the |
; variable that we are defining |
(letrec ( |
[ fn (lambda (x) |
(if (AtBase? x) (BaseCase x) |
(Combine x (fn (Decomp x))))) ] ) |
|
fn)) |
|
(define fn (gen-fn-lin AtBase? BaseCase Combine Decomp)) |
|
; Continuation passing style |
|
(define (gen-fn-lin-cc AtBase? BaseCase Combine Decomp) ( |
(letrec ( |
[ fn-cc-r (lambda (x cc) |
(if (AtBase? x) |
; compute the base case, and then continue |
(cc (BaseCase x)) |
; recurse, and then combine the result, and continue. Note |
; this is tail recursive in fn-cc-r |
(fn-cc-r (Decomp x) (lambda (result) (cc (Combine x result)))) |
) ) ] |
) |
|
; start the recursion with the identity continuation |
(lambda (x) (fn-cc-r x (lambda (r) r)) ) |
))) |
|
(define fn-cc (gen-fn-lin AtBase? BaseCase Combine Decomp)) |
|
(fn 3) |
(fn-cc 3) |
|
(define fm (gen-fn-lin AtBase? (lambda (x) 42) Combine Decomp)) |
(fm 1) |
(fm 2) |
#lang racket |
|
; a binary numeric tree is a |
; leaf vertex - which is a single element list containing a number |
; internal vertes - which is a 2-element list, each element being |
; a binary numeric tree. |
|
; constructors are not needed since we just use list operations, and |
; we are being lazy. |
(define (MakeLeaf v) (list v)) |
(define (Join t0 t1) (list t0 t1)) |
|
; fetch Left and Right subtrees |
(define Left (lambda (tree) (first tree))) |
(define Right (lambda (tree) (second tree))) |
(define Value (lambda (tree) (first tree))) |
|
; is the tree a leaf? |
(define AtBase? (lambda (tree) (null? (rest tree)))) |
; if so, you can fetch the leaf value |
(define BaseCase (lambda (tree) (first tree))) |
; if not, you can add together the two subtrees |
(define Combine (lambda (tree l r) (+ l r))) |
|
(define val (lambda (tree) |
(if (AtBase? tree) (BaseCase tree) |
(Combine tree (val (Left tree)) (val (Right tree))) ))) |
|
(define val-cc (lambda (tree cc) |
(if (AtBase? tree) (cc (BaseCase tree)) |
(val-cc (Left tree) |
(lambda (lval) (val-cc (Right tree) |
(lambda (rval) (cc (Combine tree lval rval))))))) |
)) |
|
(define t '( (1) ( (2) (3) ))) |
(val t) |
(val-cc t (lambda (x) x)) |