J Pharm Pharmaceut Sci (www.cspscanada.org) 9(2):210-221, 2006
Predicting Caco-2 Permeability Using Support Vector Machine and Chemistry Development Kit
Ma Guangli, Cheng Yiyu
Pharmaceutical Informatics Institute, Zhejiang University, Hangzhou, China.
Received, March 28, 2006; Accepted, July 11, 2006; Published, July 11, 2006.
Corresponding Author: Dr. Cheng Yiyu Telephone: 86-571-879-51138; Fax: 86-571-879-51138; E-mail: chengyy@zju.edu.cn
ABSTRACT: PURPOSE: To predict Caco-2 permeability is a valuable target for pharmaceutical research. Most of the Caco-2 prediction models are based on commercial or special software which limited their practical value. This study represents the relationship between Caco-2 permeability and molecular descriptors totally based on open source software. METHODS:The Caco-2 prediction model was constructed based on descriptors generated by open source software Chemistry Development Kit (CDK) and a support vector machine (SVM) method. Number of H-bond donors and three molecular surface area descriptors constructed the prediction model. RESULTS:The correlation coefficients (r) of the experimental and predicted Caco-2 apparent permeability for the training set and the test set were 0.88 and 0.85, respectively. CONCLUSION: The results suggest that the SVM method is effective for predicting Caco-2 permeability. Membrane permeability of compounds is determined by number of H-bond donors and molecular surface area properties.
INTRODUCTION
Over the past 10 years, much attention has been paid to absorption, distribution, metabolism, and elimination (ADME) screening, because of the important role of ADME screening in modern drug development. Many in vitro ADME screening methods have been applied to boost drug discovery process in pharmaceutical industry. Although in vitro ADME screening methods are high performance compared with in vivo ADME screening protocols, they are still resource-intensive and time-consuming. To further improve ADME screening, various in silico screening methods (ADME in silico) have been constructed (1-3), for e.g. human oral absorption (4-7), bioavailability (8, 9), metabolism (10, 11), P-glycoprotein substrates (12, 13).
Since oral is the most favorite way in various routines for drug delivery, estimating human oral bioavailability of candidates in the early stage of the drug development process is important and necessary for lead selection and optimization. Screening for absorption ability is an important part of assessing oral bioavailability and attracts efforts from industry and academia. In several in vitro cell culture models for drug absorption, the cell line most widely used is Caco-2 cells (14). These are well-differentiated intestinal cells derived from human colorectal carcinoma. These cells retain many morphological and functional properties of the in vivo intestinal epithelial cell barrier, which makes the Caco-2 cell monolayer an important model for in vitro absorption screening. Extensive studies have revealed that the human oral absorption of compounds is related to Caco-2 permeability (15). Thus, Caco-2 permeability is a valuable index for assessing oral absorption of compounds, which, in turn, calls for the methods for predicting chemical Caco-2 permeability.
Research on predicting Caco-2 permeability from structures of compounds using quantitative structure property relationship (QSPR) modeling is on the way. Some studies are summarized in Table 1. In these studies, various types of molecular descriptors were employed such as dynamic polar surface area (PSAd), HBA, HBD, MW, logP, logD, high charged polar surface area (HCPSA), radius of gyration (rgyr), RB, and membrane-interaction descriptors. Most of the Caco-2 permeability prediction models were based on linear methods such as linear regression, multiple linear regression (MLR), or partial least squares (PLS). They generally used small sets of molecules and were not fully validated by external test sets. Fujiwara et al introduced neural networks to enhance regression ability of Caco-2 permeability prediction models (21). Given the common recognition that statistical significance of a QSAR/QSPR model does not imply its practical applicability, a validation using external test sets of molecules is necessary. Hou et al collected several published data sets and investigated the relationship between simple descriptors and Caco-2 permeability(23). Most of the models were built by commercial or special software packages such as SYBYL(23, 25) and VolSurf (11), which limited the usage and validation of the models by other researchers.
In this study, Caco-2 permeability prediction models based on MLR and SVM methods were built. All of the molecular descriptors involved were calculated by open source software, CDK and statistical work was done by open source software, R. Open source means that the software is free and the users can read, modify and add functions to the source code freely. This means those who want to validate or use the models described here to predict Caco-2 permeability from the chemical structure can do so. Furthermore, the models provided some insight into physiochemical process. Because Caco-2 penetration mentioned here was passive transport, metabolism and active transport was out of the scope of this study.
MATERIALS AND METHODS
Software and Hardware
The chemistry development kit (CDK) is a freely available open source Java library for structural chemistry and bioinformatics. Its development is an open source project by a team of international collaborators from academic and industrial institutions. CDK provides methods for many tasks in molecular informatics, such as 2D and 3D rendering of chemical structure, I/O routines, SMILES parsing and generation, ring searches, isomorphism checking, structure diagram generation, and energy minimization (26). In the recent update, CDK provides QSAR modeling functions which included more than 30 routines to calculate descriptors and an interface to open source statistical software, R (27).
If the software involved in QSAR/QSPR modeling is commercial, the validation and usage of the models is limited for the other researchers. The CDK project provides not only source code but also references to dictionaries that describe the exact algorithm used, and versioning of the implementation of the algorithm, which makes academic research more valuable to both academics and industry (28).
The descriptors studied in this work were generated by CDK version 20050826. The CDK and R were linked by SJava 0.8 on Linux Redhat Workstation 4.0, Compaq Evo N600C. The statistical methods were provided by R version 2.2.0. Data manipulation and model scripts in R were written.
Data Set
The experimental apparent Caco-2 ........ permeability(logPapp) data of 100 drugs was collected from the literature (23). To compare with Hou et al’s work, the data set was separated into a training set of 77 compounds and a test set of 23 compounds as in Hou et al (23). The training set was used to build model, and the test set was used to evaluate its predictability. The experimental apparent permeability, the molecular descriptors used in this study and the results predicted by the multiple regression model (MLR) and the support vector machine (SVM) model were listed in Table 2.
Descriptors
Descriptors play a vital role in QSAR/QSPR models. Simple and meaningful descriptors make QSAR/QSPR models understandable and useful for drug development. The descriptors available in the current version CDK are separated into 5 classes: constitutional, topological, geometric, electric, and hybrid (28) as shown in Table 3. Further information about the descriptors and CDK can be found on the web site (http://cdk.sf.net). That CDK provides a wide range of descriptors makes predicting Caco-2 permeability possible.
Correlation between membrane permeability and some descriptors was impossible or difficult to be understood and explained. These descriptors were removed from the data set. They were Chi series, eccentric connectivity, Kier value, Petitjean number, VAdjMa, Winer number, Zagre index, geometrical descriptors, BCUT class and WHIM class descriptors.
COMPUTATIONAL METHODS
Genetic algorithm (GA)
As a stochastic search technique, genetic algorithm (GA) based on the principle of natural evolution, was widely used in pharmaceutical, chemical and bioinformatical investigations (3, 29-33). Haupt et al explained this technique from a practical point of view (34). Genetic algorithms are categorized into binary and continuous classes.
Binary GA used to select descriptors was extensively studied in recent investigations (35, 36). Continuous GA was employed to determine the optimal SVM parameters (37). In this paper, Binary GA was used to select variables from descriptors generated by CDK to build MLR and SVM models, respectively. Continuous GA optimized the SVM parameters to achieve best Caco-2 permeability prediction performance.
The core of the optimization problem is the evaluation function. The evaluation functions for descriptors selection were given below arbitrarily.
MLR: eva=2-rtraining-0.1rtest+0.01N
SVM: eva=2-rtraining-rtest+0.015N
where eva is the evaluation value. rtraining is the correlation coefficient of experimental and predicted values for training set. rtest is the correlation coefficient of experimental and predicted values for test set. N is number of descriptors. 0.01 N and 0.015 N are penalty components to reduce the number of descriptors selected into the models.
Table 1: Summary of Several Caco-2 Permeability Prediction Investigations
Year |
Authors |
Method |
Software |
Descriptors |
1996 |
Palm et al(16) |
Linear Regression |
PCMODEL, MacroModel |
Dynamic polar surface area (PSAd) |
1997 |
Norinder et al(17) |
PLS |
MolSurf |
Surface, logP, Polarity, HBAoa, HBDb, HBA, HBD, etc. |
1998 |
Camenisch et al(18) |
Non-linear Regression |
Statistica (statistical software) |
MW, logD(oct)c |
2000 |
Pickett et al(19) |
Not Mentioned |
Chem-X, SYBYL |
ClogPd, MW, PSAe |
2000 |
Cruciani et al(11) |
PLS |
VolSurf |
VolSurf Descriptors |
2002 |
Kulkarni et al(20) |
membrane-interaction QSAR(MI-QSAR) |
Chemlab-II, Mopac 6.0 |
Solute aqueous dissolution and salvation descriptors, Solute-membrane interaction and salvation descriptors, General intramolecular solute descriptors. (Many descriptors) |
2002 |
Fujiwara et al(21) |
Molecular orbital (MO) calculation, |
MOPAC97 |
Dipole moment, Polarizability, Sum(N)f, Sum(O)g, Sum(H)h |
2002 |
Yamashita et al(3) |
Genetic Algorithm Based Partial Least Squares |
Molconn-Z 3.50 |
Molconn-Z descriptors |
2003 |
Ponce et al(22) |
MLR |
TOMO-COMD |
Quadratic Indices |
2004 |
Hou et al(23) |
MLR |
SYBYL, SASA, MSMS, etc. |
HCPSAi, logD, rgyrj, RB |
2004 |
Ponce et al(24) |
Linear discriminant analysis (LDA) |
TOMO-COMDStatistica 5.5 |
Quadratic Indices |
2005 |
Refsgaard et al(25) |
Nearest-Neighbor classification |
SYBYL, Matlab |
Number of flex bonds, number of hydrogen bond acceptors and donors, molecular and polar surface area |
a Hydrogen bond acceptor strength for oxygen atoms. b Hydrogen bond donor strength. c distribution coefficient in 1-octanol/water. d Calculated logP. e Polar surface area. f Sum of charges of nitrogen atoms. g Sum of charges of oxygen atoms. h Hydrogen atoms bonding to nitrogen or oxygen atoms. i High charged polar surface area. j Radius of gyration.
Table 2: Data of Experimental Apparent Permeability, Molecular Descriptors, and Predicted Results
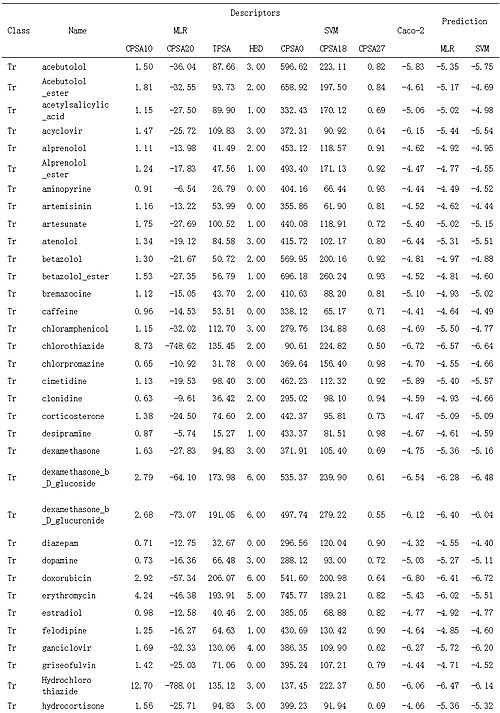
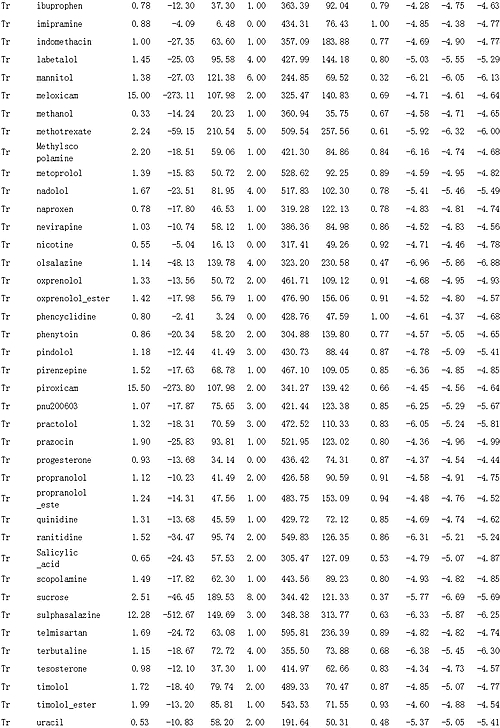

Tr is training set; Te is test set.
Table 3: Descriptors Implemented by CDK Version 20050826
CDK version 20050826 |
||||
Topological |
Geometrical |
Constitutional |
Hybrid |
Electronic |
Chi0, Chi0C, Chi0v, Chi0vC, Chi1, Chi1C, Chi1v, Chi1vC, EccentricConnectivity, KierValues, PetitjeanNumber, TPSA, VAdjMa, WienerNumber, ZagrebIndex |
GravitationalIndex, MomentOfInertia |
Apol, AromaticAtomsCount, AromaticBondsCount, Bpol, Lipinskifailures, RotatableBoundsCount, XlogP |
BCUT, CPSA, WHIM |
HBondDonors, HBondAcceptors |
Support vector machine (SVM)
In addition to descriptor selection, computational method selection is another critical step for QSAR/QSPR modeling. MLR, PLS, Nearest-Neighbor classification and neural networks were utilized to address Caco-2 permeability prediction as shown in Table 1. Support vector machine (SVM), developed by Vapnik, as a novel type of machine learning (38), was widely used to solve classification and regression problems on human oral absorption (39), solubility (40), P-glycoprotein substrate s(41), blood-brain barrier penetrating and nonpenetrating agents (13), and metabolism (42). SVM was employed to fit a non-linear relationship between the Caco-2 permeability and the CDK descriptors.
The regression performances of SVM depend on several factors: cost of constraints violation (cost), epsilon in the insensitive-loss function (epsilon), the kernel type and its parameters. A Radial Basis Function (RBF) was chosen to be the kernel function because it is widely used in regression problems. The three parameters, cost, epsilon, and gamma, used to construct the final Caco-2 permeability prediction model were 3.37, 0.1, and 0.61.
RESULTS
The CDK descriptors selected by GA to construct MLR and SVM model were listed in Table 4. That HBD appeared in both the MLR model and the SVM model suggested that HBD is an important factor to membrane permeability. This conclusion is supported by the references . The relationship between membrane permeability and molecular surface area properties especially PSAd, were extensively studied (16, 17, 19, 23, 25). Topological polar surface area (TPSA) as a form of PSAd was selected into the MLR model. CDK provided a class of descriptors, CPSA, to describe charged partial surface area properties. In both the MLR model and the SVM model, CPSA descriptors played vital roles to predict Caco-2 permeability presented by Table 4.
Multiple linear regression (MLR) Model
A multiple linear regression (MLR) model was built to predict Caco-2 permeability with four CDK descriptors:
logPapp=-0.18HBD+0.095CPSA10+0.0026CPSA20-0.0051TPSA-4.42
Table 4: Symbols and Explanation of Descriptors to Construct MLR and SVM models
Model |
Symbols |
Meaning |
MLR |
CPSA10 |
Partial positive surface area*total positive charge on the molecule/total molecular surface area |
CPSA20 |
Charge weighted partial negative surface area*total molecular surface area/1000 |
|
TPSA |
Topological polar surface area based on fragment contributions |
|
|
HBD |
Number of H-bond donors |
SVM |
CPSA0 |
Sum of surface area on positive parts of molecule |
CPSA18 |
Partial negative surface area* total molecular surface area/1000 |
|
CPSA27 |
Sum of solvent accessible surface areas of atoms with absolute value of partial charges less than 0.2/total molecular surface area |
Table 5: Distribution of Experimental Apparent Permeability and Each Molecular Descriptor
|
|
|
Descriptors |
||||||
Class |
|
Caco2 |
CPSA10 |
CPSA20 |
TPSA |
HBD |
CPSA0 |
CPSA18 |
CPSA27 |
Training |
Min |
-6.96 |
0.33 |
-788.01 |
3.24 |
0.00 |
90.61 |
35.75 |
0.32 |
Mean |
-5.14 |
2.09 |
-54.45 |
78.28 |
2.12 |
411.24 |
125.95 |
0.77 |
|
Max |
-4.28 |
15.50 |
-2.41 |
210.54 |
8.00 |
745.77 |
313.77 |
1.00 |
|
Test |
Min |
-6.88 |
0.45 |
-560.13 |
23.55 |
0.00 |
250.54 |
59.22 |
0.54 |
Mean |
-5.33 |
4.35 |
-102.44 |
106.32 |
2.17 |
475.88 |
174.87 |
0.77 |
|
Max |
-4.11 |
20.82 |
-6.35 |
278.80 |
5.00 |
1228.88 |
472.46 |
0.95 |
|
Table 5 summarizes the distribution of the descriptors calculated by CDK for the compounds used in this study. This dataset consists of compounds that were very different in structure and membrane permeability. Each descriptor of the compounds covered a wide range.
Table 6: Correlation Coefficients (r) between Experimental Apparent Permeability and Each MLR Descriptor for The Training Set
HBD |
CPSA10 |
CPSA20 |
TPSA |
|
Caco2 |
-0.65 |
-0.19 |
0.33 |
-0.65 |
HBD |
|
0.16 |
-0.13 |
0.81 |
CPSA10 |
|
|
-0.81 |
0.41 |
CPSA20 |
|
|
|
-0.37 |
The Hou’s MLR model based on fraction of rotatable bonds (frotb), logD, high charged polar surface area (HCPSA) and radius of gyration (rgyr) was rebuilt, while the limitation of logD<2.0 was cut out (23). The r of Hou’s model in the training set and the test set were 0.81 and 0.70. The r showed that the four descriptors generated by CDK had equivalent regression and prediction ability as Hou’s four descriptors without the limitation of logD<2.0.
Support Vector Machine (SVM) Model
MLR did not give the satisfied results as shown in Figure 1. It was believed that there exist nonlinear relationship between Caco-2 permeability and CDK descriptors. Hence, SVM method as a good nonlinear regression algorithm, was employed. The correlation coefficients between Caco-2 permeability and each descriptor used in SVM model were listed in Table 7. The relationship between experimental logPapp and predicted values might be nonlinear. The results of Spearman test was also support the SVM model as listed in Table 8.
Table 7: Correlation Coefficients (r) between Experimental Apparent Permeability and Each SVM Descriptor for The Training Set
HBD |
CPSA0 |
CPSA18 |
CPSA27 |
|
Caco2 |
-0.65 |
0.07 |
-0.37 |
0.52 |
HBD |
|
0.08 |
0.37 |
-0.62 |
CPSA0 |
|
|
0.28 |
0.51 |
CPSA18 |
|
|
|
-0.20 |
Table 8: Summary of Spearman Test Results for Training and Test Data Set
Class |
|
Valid N |
Spearman R |
p-level |
Training |
MLR |
77.00 |
0.71 |
0.00 |
SVM |
77.00 |
0.85 |
0.00 |
|
Test |
MLR |
23.00 |
0.78 |
0.00 |
SVM |
23.00 |
0.85 |
0.00 |
The correlation coefficients (r) of experimental logPapp and predicted values by the SVM model were 0.88 and 0.85 for the training set and the test set, respectively. The SVM model was the final model. Figure 1 shows that while experimental logPapp<-5, the values predicted by the MLR and SVM models were larger than the experimental values.
The SVM method was also applied to Hou’s four descriptors. The correlation coefficients (r) of experimental logPapp and predicted values for the training set and the test set were 0.92 and 0.77, respectively. The regression ability of Hou’s four descriptors was increased remarkably, which proved SVM’s regression ability. This also proved that the four descriptors generated by CDK were equivalent compared with Hou’s four descriptors for Caco-2 permeability prediction, when a non-linear modeling technique is used.
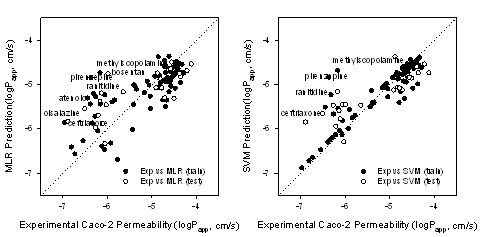
Figure 1: Correlation between experimental Caco-2 permeability and the predicted values by the MLR and SVM models.
Most of the Caco-2 permeability prediction investigations were based on a small training set of molecules and no external test set but Hou et al(23) and Refsgaard et al (25). Refsgaard et al has built a classification model based on in-house data which could not be compared with this study. Because Hou’s data set used in this study, it was convenient to compare with the results of Hou’s work and Ponce’s work mentioned in the literature (23). The results of the comparison are listed in Table 9. Unsigned mean error, UME, we calculated from Hou’s data was 0.45, not 0.49. According to the comparison results, the SVM model based on CDK descriptors were significantly better than Hou’s and Ponce’s model significantly.
Table 9: Summary of Predicted Values by Hou's, Ponce's and SVM model |
|||||
Compound |
Caco-2a |
Prediction |
|||
MLRb |
SVMc |
Hou'sd |
Ponce'se |
||
bosentan |
-5.98 |
-5.43 |
-5.29 |
|
|
ceftriaxone |
-6.88 |
-5.32 |
-5.48 |
|
|
coumarin |
-4.11 |
-4.44 |
-4.54 |
|
|
amoxicillin |
-6.1 |
-5.65 |
-5.84 |
-6.16 |
|
antipyrine |
-4.55 |
-4.45 |
-4.51 |
-4.82 |
|
cyclosporine |
-6.05 |
-5.82 |
-5.39 |
-5.81 |
|
enalapril |
-5.64 |
-5.04 |
-4.89 |
-5.66 |
|
epinephrine |
-6.02 |
-5.56 |
-5.72 |
-5.47 |
|
diltiazem |
-4.38 |
-4.57 |
-4.87 |
-4.84 |
-3.17 |
fleroxacin |
-4.81 |
-4.76 |
-4.87 |
-5.39 |
-3.95 |
furosemide |
-6.5 |
-5.81 |
-5.67 |
-5.81 |
-8.74 |
guanabenz |
-4.5 |
-5.24 |
-5.35 |
-4.63 |
-6.68 |
guanoxan |
-4.71 |
-5.27 |
-5.41 |
-5.39 |
-6.69 |
lidocaine |
-4.21 |
-4.75 |
-4.67 |
-4.45 |
-4.83 |
mibefradil |
-4.87 |
-4.97 |
-4.74 |
-5.06 |
-4.83 |
nitrendipine |
-4.77 |
-4.73 |
-4.93 |
-5.08 |
-4.87 |
proscillaridin |
-6.2 |
-5.77 |
-5.27 |
-5.42 |
-5.63 |
remikiren |
-6.13 |
-6.17 |
-5.53 |
-5.36 |
-8.33 |
saquinavir |
-6.26 |
-5.87 |
-5.55 |
-5.39 |
-9.32 |
sulpiride |
-6.16 |
-5.47 |
-5.13 |
-5.81 |
-7.76 |
theophylline |
-4.35 |
-4.66 |
-4.74 |
-5.06 |
-4.65 |
tiacrilast |
-4.9 |
-4.97 |
-4.9 |
-5.68 |
-3.89 |
verapamil |
-4.58 |
-4.52 |
-4.84 |
-4.87 |
-3.17 |
r (Ponce's Set) |
|
0.79 |
0.84 |
0.74 |
0.78 |
UME(Ponce's Set) |
|
0.46 |
0.44 |
0.52 |
1.29 |
r (Hou's Set) |
|
0.79 |
0.83 |
0.78 |
|
UME(Hou's Set) |
|
0.43 |
0.42 |
0.45 |
|
r (whole set) |
|
0.76 |
0.85 |
|
|
UME (whole set) |
|
0.49 |
0.46 |
|
|
a Caco-2, experimental Caco-2 apparent permeability (cm/s), logPapp; bPrediction by the MLR model described in this paper. c Prediction by the SVM model described in this paper. d Prediction by Hou’s model. e Prediction by Ponce’s model. UME is unsigned mean error. |
|||||
CONCLUSION
In the current study, Caco-2 permeability prediction models based on MLR, SVM and CDK descriptors were developed. The previous investigations on Caco-2 permeability prediction and the MLR model described in this paper suggested the nonlinear relationship between descriptors and Caco-2 permeability. The SVM method assigned CDK descriptors nonlinear regression ability to achieve good performance in Caco-2 permeability prediction, which implies that SVM method is an effective algorithm for Caco-2 permeability prediction. The descriptors selected in the MLR or SVM model represent that Caco-2 or membrane permeability is determined by number of H-bond donors and molecular surface area properties.
At last, this SVM model is not perfect, because the data set and descriptors used here were limited. A larger data set could make the model better for prediction and cover larger chemical space. That the whole work was based on open source software CDK makes everybody in pharmaceutical area free to use, rebuild models and even develop QSAR/QSPR software. The modeling investigation of oral absorption, distribution, and clearance prediction based on this work was conducted.