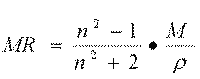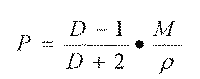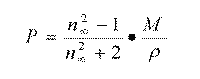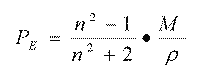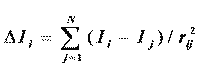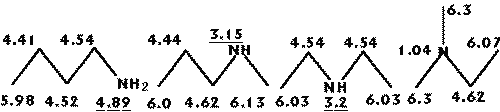J Pharm Pharmaceut Sci (www.ualberta.ca/~csps) 7(1):19-26, 2004
Definition of a novel atomic index for QSAR: the refractotopological state.
Ramon Carrasco-Velar
Pharmaceutical Chemistry Center, Atabey, Playa Aptdo, La Habana, CubaJ. A. Padrón
Faculty of Chemistry, Havana University, CubaJ. Gálvez
Chemical-Physics Department, Valencia University, SpainReceived 23 January 2003, Revised 25 November 2003, Accepted 9 January 2004, Published 23 January 2004
PDF Version
Abstract
PURPOSE. In this work, a novel descriptor of atoms in molecules is introduced. The Refractotopological State Index for atoms (R-state,Â), rectifies the atomic refractivity values reported by Crippen et al with the atomic refractivity values of the topological environment of each skeletal atom in the molecule. METHOD. The R-state (Âi ), for atom i is an hybrid index that is defined as the intrinsic refractivity value of the atom i (ARi) plus a perturbation term ∆ ARi in the non-hydrogen depleted graph. RESULTS. The variations of the  values in different molecules are showed. QSAR examples previously reported by other authors are given for benzimidazole inhibition of Lee strain flu virus and receptor binding affinity of b -carbolines. CONCLUSIONS. The index does not only describe the representation of the atomic dispersive forces related to the molar refractivity but also the influence of bounded and unbounded atoms as a measure of the distance-effect of the other groups in the molecule. The R-state index has proved a good performance, either alone or combined with the electro topological (E)-state index. This implies that in those cases this representation of dispersive forces between the molecule and the active site is a valid approach to the biological problem.
Introduction
The final objective of any quantitative chemical structure-biological activity relationship (QSAR) is to portray the receptor by the structural, physicochemical and biological properties of the ligand. It is common knowledge that the relationship between the binding energy of the ligand (related to the molecular forces involved in binding) with different physicochemical properties for different parts of the ligand can be establish. Therefore, the identification of the appropriate physicochemical property for each molecular force is an important task.
On the other hand, a central concept in chemistry states that the properties of a molecule are intimately related to its molecular structure. The molecular skeleton is frequently used to obtain information about the number and kinds of atoms and the connections between them. The pattern of these connections within the skeleton is what actually determines the three-dimensional architecture of any molecule. To establish a QSAR model it is necessary not only to completely define the molecular structure, but also the influences governing measured values of the physical properties or biological activities. The electronic features of the molecules are portrayed by molecular orbital calculations and the descriptors include the net charge on the atoms, the energy of frontier orbitals, maps of electrostatic potentials, etc. The second feature of the chemical structure's influences is broadly described by a great number of numerical indices associated to the skeleton itself of a compound as a whole, or to a fragment of it. Most of these indices are based on chemical graph theory (1).
An index that includes both of these features of structural attributions intrinsic to a molecule is the electrotopological state index for atoms in a molecule (2-4). This index recognizes that every atom in a molecule is unique, and this uniqueness arises from differences in the electronic and topological environment of each atom (4). This descriptor is formulated as an intrinsic value Ii plus a perturbation given by the electronic influence of the topological environment of the molecule.
One of the most important chemico-physical properties used in QSAR studies is the molar refractivity (MR). It has been shown to be related to lipophilicity, molar volume and steric bulk (5). The importance of splitting the MR into its atomic components for QSAR studies oriented to three-dimensional molecules was demonstrated by Crippen et al (6-7). A method for the estimation of molar refractivity, based on the assignment of 22 atomic contributions obtained by classification of each atomic fragment according to the number and nature of the connected atoms to it, was developed by those authors (8-9). The reported correlation coefficient between observed and predicted values of the property using this method is greater than 0.999, with standard deviations values of 0.774(8). This method has been widely used for MR estimation and QSAR studies. However, the atomic contributions to MR are not suitable as one-atom descriptors for QSAR studies since they do not change when the chemical environment is changed, for example if a substitution occurs.
Recently, a molecular index based on a combination of these same values of atomic refractivity was defined. (10) The capability of this index to afford good results in QSAR studies was demonstrated. In this paper, we propose a Refractotopological State (R-state, ℜ ) descriptor of atoms in molecules. This index corrects the atomic refractivity values reported by Crippen et al using the atomic refractivity values of the topological environment of each skeletal atom in the molecule as in the Electrotopological State index defined by Kier and Hall (2-4). The applicability of this index in QSAR studies is also demonstrated.
mOLAR rEFRACTIVITY AND pOLARIZABILITY
Molar refractivity
The molar refractivity is a constitutive-additive property that is calculated by the Lorenz-Lorentz formula (eq. 1):
where M is the molecular weight, n the refraction index and r the density, which, at a given temperature, depends only on the wavelength of the light used to measure the refraction index. For a radiation of infinite wavelength, the molar refractivity represents the real volume of the molecules contained in one mole of the substance.
Polarizability of the molecules.
The electrons and nuclei of molecule are mobile to a limited degree. For that reason, when a polar or non-polar molecule is placed in an electric field a small displacement of the charge will take place. As a result, a dipole would be introduced in the molecule, in addition to the permanent one that may exist.
The molar polarization is given by:
where P is the molar polarization, induced polarization or polarization of distortion and D is the dielectric constant of the environment. As D is an abstracted number, P represents a molar volume. This equation, called Mosotti-Clausius equation is only an approximation. In 1831, Maxwell related the dielectric constant with the refraction index measured at long wavelength:
and equation 2 becomes:
where the right term of the equation [4] is the molar refractivity measured at long wavelengths and the magnitude is the average polarizability of a non-polar molecule in an electric field.
Therefore, the value of n¥ cannot be obtained by extrapolation to infinite wavelengths starting from the refraction indexes measured with visible light, because this radiation can only displace electrons, while the positively loaded nuclei remain without changes. In fact, if n is the refraction index measure using visible light, then:
where PE is the electronic polarization. This is similar to the molar refractivity measure using visible light and represents the part of the total induced polarization P caused by the distortion or deformation of the molecule electronic cloud. This deformation originates from the presence of instantaneous dipoles of an approaching ligand. That is why the molar refractivity is related not only to the volume of the molecules, but also to the London dispersive forces that, for instance, play a key role in the drug-receptor interaction.
The atomic contribution to molar refractivity calculated by the Ghose and Crippen method.
In order to model the dispersive interactions, Ghose and Crippen defined 110 atom types, (6-8) representing most commonly occurring atomic states of carbon, hydrogen, oxygen, nitrogen, halogens, and sulphur in organic molecules. They stated that this classification partially differentiates the polarizing effects of heteroatoms and the effect of overlapping with non-hydrogen atoms, although they accepted that this classification might be weak in differentiating the conjugation effects. In the explanation of their method of calculation, the authors said that the classification may not completely cover all organic molecules, and that the addition of atom types is possible. Further on, the 110 atom types were reduced to 22. The evaluation of the individual atomic value is based on the idea that the sum of the atomic values (ai) being related to the molecular value of the molar refractivity:
The Electrotopological State Index (E-State)
The electrotopological state index (E-state) is developed from chemical graph theory and uses the chemical graph (hydrogen-suppressed skeleton) for generation of atom-level structure indices. The index is based on the electronic effect of each atom on the other atoms in the molecule as modified by molecular topology (2-4). Each atom has an assigned intrinsic state value Ii calculated as follows:
where N is the principal quantum number of the atom i, δ v the number or valence electrons in the skeleton (Zv -h), and δ the number of s electrons in the skeleton ( s -h). For a skeleton atom, Zv is the number of valence electrons, s the number of electrons in s orbitals, and h the number of bounded hydrogen atoms. The E-state S (Ai ) for the atom is the modified intrinsic value:
where ∆ Ii quantifies the perturbing effect on the intrinsic atom value. This perturbation is assumed to be a function of the difference in the intrinsic values Ii and Ij :
where rij is the number of atoms in the shortest path between atoms i and j including both i and j . The difference in intrinsic values, ∆ Ii, for a pair of skeletal atoms encodes both electronic and topological attributes that arise from electronegativity differences and skeletal connectivity. Derived from this electronegativity difference, the E-state value for an atom is related but not limited to the concept of atomic partial charge.
The Refractotopological State Index (R-State).
The refractotopological state index R-state is developed from the chemical graph theory and the partition of the molar refractivity defined by Ghose and Crippen. The index is based on the influence of dispersive forces of each atom on the other atoms in the molecule, modified by molecular topology.
Âi Definition
The R-state (Âi), for atom i is defined as follows,
where ARi is the intrinsic refractivity value of the atom i, and ∆ ARi is a perturbation term defined by:
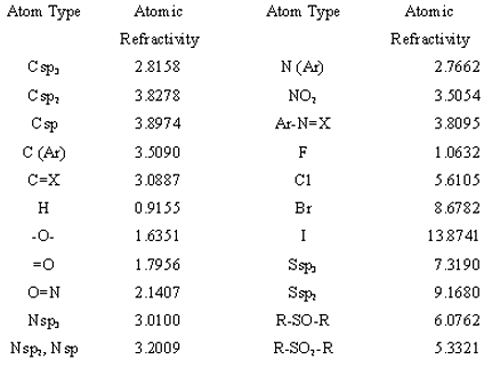
where the sum is all over j adjacent vertices in the graph, ARi and ARj are the intrinsic refractivity values of the atoms i and j respectively, and rij2 is the number of atoms in the shortest path between atoms i and j including both i and j that's to say, the distance between atoms counted as the graph distance ( dij ) plus one (2-4). As in the E-state, this quadratic topological distance, indicates that there must be a decrease in the interaction effect with the separation distance between atoms. Atomic refractivity values (7) used in the analysis is shown in table 1. The intrinsic values of the refractivity for each one of the heavy atoms include the atomic refractivity value of the hydrogen atoms bonded to them.
Table 1: Atomic refractivity values used in the analysis.
Method of calculation.
In all cases Âi index calculation involves three steps: (a) molecular structure generation, (b) classification of the atom types according to the 22 reported types (table 1) and (c) Âi index calculation. The RIGA program (10) and software developed in the author's laboratories were used to perform the (a), (b) and (c) steps, respectively. The STATISTICA v.4.0 software was used in all the statistical analysis of the data (11).
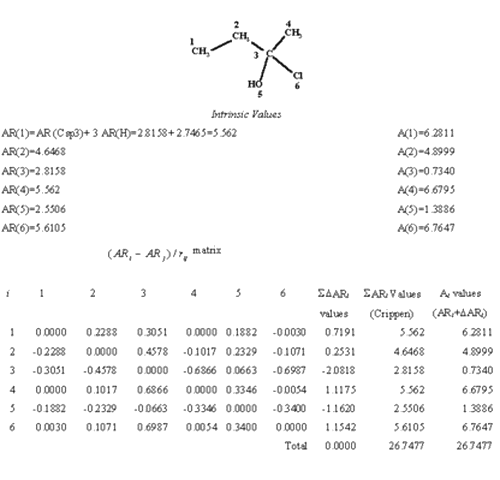
To illustrate the calculation steps of the index the procedure is shown in table 2 for 2-chloro-2 butanol.
Table 2: Refractotopological state calculation for 2-chloro-2 butanol.
Note that the sum of the R-state index of all the atoms (Ai ) in the molecule is equal to the sum of the intrinsic atomic contribution values (S ARi), but the value itself is rather dissimilar. Using this approach the methyl groups 1 and 4 are marked as non equal as expected since their environments are different and the dispersive forces in the methyl group 4 should be higher because of the number and nature of the groups present in that part of the molecule. It is also relevant the decrease of the value on the atom number 3, which is buried in the skeleton and hence unable to have a direct interaction with a hypothetical active site or molecule from a dispersive-sterical point of view.
Examples and Discussion
When compared to other topological methods, which do not consider the influence of the hydrogen bonded to the atoms, this index includes this influence on the intrinsic values of the heavy atoms. According to the nature of the studied phenomenon, this inclusion reflects the total interaction volume of the group with the protein ligand and it is important not only to the intrinsic value of the direct bonded atom but also to other groups present on the molecule.
Effect of the position. Buried atoms.
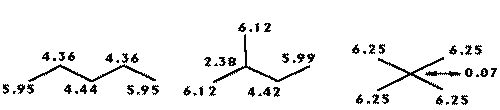
The index presents a large decrease on its value as the atom changes from primary to quaternary as represented in figures 1 and 2, where a series of pentanes and amines are presented along with the R-state values for each skeletal atom.
Figure 1: Changes on the R-state values in pentane isomers.
Figure 2: Changes on the R-state values in amines.
Due to the nature of the dispersive forces, it is logical that an atom will interact less with the protein ligand as it becomes buried in the skeleton and hence a smaller total interaction volume. Note that the amine group R-state values reflect changes following small variations on its position.
Figure 3 shows R-state values for alcohols. As the OH group has an R-state intrinsic value lower than the methyl group, its value is influenced accordingly.
Figure 3: hanges on the R-state values in alcohols.
Effect of the atom nature in aromatic compounds.
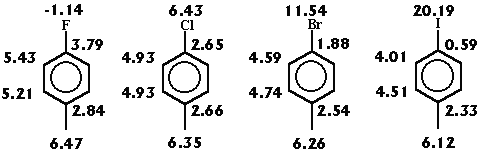
In figure 4 a series of halo-substituted toluenes is shown. The effect of changing the halogen substituents is reflected by the R-state values: the higher values correspondent to the less electronegative groups.
Figure 4: Changes on the R-state values in halogen toluene derivatives.
Effect of the position isomers in aromatic compounds.
The R-state index is also able to portray the changes on the relative position, as is shown on figure 5. These changes affect not only the halogen atom but also the different atoms in the molecule. For example, the more buried C1 , the less corresponding value of the index.
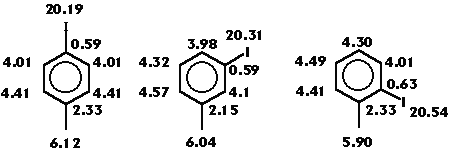
Figure 5: Changes on the R-state values in iodotoluene isomers.
Application to QSAR Studies
Receptor binding affinity of b -carbolines.
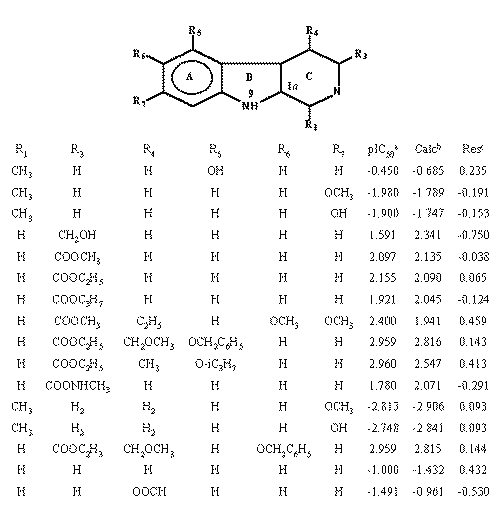
To test the capability of the index to describe interactions in active sites, the receptor binding of a series of b -carbolines was investigated (12). The affinities were determined by the drug displacement of 50% of 3H-flunitrazepam from synaptosomal rat membranes (pIC50 ) and are given in Table 3.
Table 3: Reported data of the binding of b-carbolines to the benzodiazepine receptor*.
*The ring C is non-aromatic, only for compounds 12 and 13. a The negative log of the IC50 value for binding. b Activity Value computed from eq. 15. c Res= pIC50-Calc.The 13 common ring atoms in all structures were calculated and the corresponding R-state values obtained were correlated with the biological activity using forward stepwise regression analysis. The obtained model was then compared with the previously reported by Kier and Hall (3).
The best one-variable model obtained by using the R-state value includes the atom 11 as independent variable (r=0.86, s=1.16, F=40, n=16). This result is worse than the reported with the use of E-state (r=0.893, s=1.03, F=55, n=16). Nevertheless, the inclusion of the R-state value of the atom 8 results in a good model (r=0.977, s=0.50, F=138, n=16), better than the two variable equation reported using E-state (r=0.92, s=0.93, F=36, n=16). The three-variable model (Eq. 12)
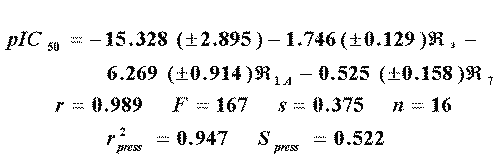
is also better than the equivalent previously reported (Eq. 13).
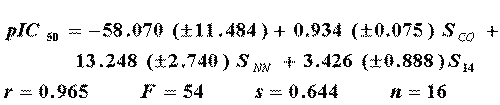
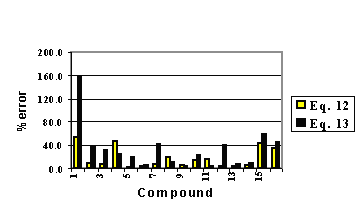
where SCO , SNN and SC14 are linear combinations of several other variables (3). In Figure 1, it can be observed the performance of the relative errors.
Our results indicate that the best distribution is achieved through Eq. 12. Only in three cases were the errors slightly higher with the use of ℜ than with E-STATE .
Figure 6: Relative errors for equations 12 and 13.
The results show that the R-state index allows for a better prediction of the binding affinities than the E-state index, therefore the dispersive forces play a predominant role in the specific interaction site between the drugs and the benzodiazepine receptor, rather than the electronic factor.
After the study, the atoms flagged, as the most relevant are those numbered 3, 1 a, and 7. Those positions reflect the changes in activity along with the different substitution patterns since they cover the B -carbolines three-ring system.
According to the results, to enhance the activity it is necessary to reduce the atom 3 R-state value and increase atoms 1a and 7 R-state values with adequate substitutions that follows this objectives.
Inhibition of Lee strain flu virus by benzimidazoles.
Another example of the use of the R-state in QSAR studies is the inhibition of Lee strain flu virus by benzimidazoles (13). This was studied after the computation of the R-state values for the seven common skeletal atoms in the series (Table 4).
Table 4: Inhibition of Lee strain flu virus by benzimidazoles.
a Experimental value for the inhibition constant. bValues computed for inhibition from eq. 14 cres=pKi-calc. dValues computed for inhibition from eq. 15 eres=pKi-calc. fValues computed for inhibition from eq. 16 gres=pKiexp- pKicalc.The regression equation and statistical parameters for the correlation biological property-R-state values are shown (Eq. 14).
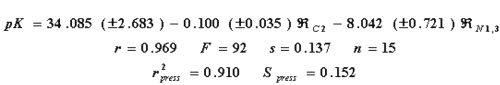
where r, s and F represent the correlation coefficient, standard deviation of regression, and Fisher ratio, respectively. The high value of the cross-validation regression coefficient ( r2press ), and the similarity of "s" and Spress , tells us about the high stability of the model. The variable ÂC2 is the R-state of the atom numbered as 2, and ÂN1, 3 is the average of the R-state values of the nitrogen atoms numbered 1 and 3. The best model previously reported is the one obtained by Hall (4), which includes the E-state values of the atom 2, and the average E-state values of the nitrogens 1 and 3 (eq. 15).
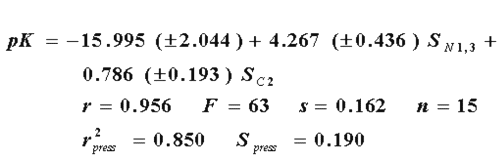
In this case, the R-state values afford a better model than the E-state values with the same variables. That is explained by the best values of each statistical parameter in the eq. 14 as compared with eq. 15.This suggests that the biological response of benzimidazoles against flu virus involve not only electrostatic interactions explained by E-state, but also local dispersive forces represented by the R-state. On the other hand, we have found that the combination of both descriptors results in an even better model (eq. 16), as can be seen in the higher values of r, F, and r2press and in the lesser values of s and Spress, respectively.
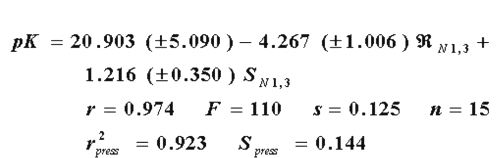
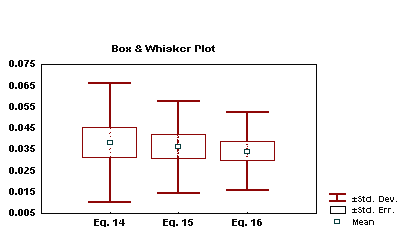
Therefore, it is possible to express the biological activity of these drugs as a combination of both electronic and dispersive forces in the interaction. In this combination there must be a balance between the dispersive value of the substituents to decrease the nitrogens 1 and 3 R-state values (negative coefficient) and the electronegativity of the substituents to increase the E-state of the same atoms (positive coefficient), in order to optimize the activity of the drugs under study. In a box and whisker plot (Figure 2), is seen that with the combined use of  and the E-state, it is possible to obtain a better quality for the relative error.
Figure 7: Box and whisker plot of the standard deviation, the standard error and the mean of the errors in equations 14, 15 and 16.
Conclusions
An index based on the correction of the atomic refractivity values, defined by Crippen et al with the atomic refractivity values of the topological environment of each skeletal atom in molecule, is proposed. The new atomic descriptor R-state promises to be useful in quantitative structure-activity relationships studies, especially in those involving dispersive atomic interactions with active sites. The index has a direct structural interpretation since it expresses the atomic contribution of an important physico-chemical property (molar refractivity) related to dispersive forces in biologically active sites and also contains topological information about the chemical structure of the atomic environment. In addition, the R-state index can be successfully used in QSAR studies with the Electrotopological State index that it is very simple to calculate since no quantum chemical calculations are involved.
Acknowledgements
This work was supported by grants from The Ministry of Science, Technology and Environment of the Republic of Cuba. R.C. thanks Dr. D. José Elguero Bertollini the helpful discussions for the conclusion of the manuscript. Thanks to M. Encinosa for his kind help and incisive critics.
References and Notes
For goods reviews on this topic see: a) Kier, L.B.; Hall, L.H. Molecular Connectivity in Chemistry and Drug Research; Academic Press, New York, 1976. b) Kier, L.B.; Hall, L.H. Molecular Connectivity in Structure-Activity Analysis; John Wiley, London, 1986. c) Trinajstic, N.; Chemical Graph Theory; CRC, Boca Ratón, FL, 1983; Vols. I and II.
Hall. L. H., Mohney, B.; Kier, L.B., The Electrotopological State: Structure Information at the Atomic Level for Molecular Graphs, J. Chem. Inf. Comput. Sci., 1991, 31, 1, 76-82.
Hall. L. H., Mohney, B.; Kier, L.B., The Electrotopological State: An Atom Index for QSAR, Quant. Struct.-Act. Relat., 1991 10, 43-51.
Kier, L.B. and Hall. L. H., An Electrotopological State Index for Atoms in Molecules, Pharmac. Res., 1990, 7, 8, 801-807.
Kubinyi, H., QSAR: Hansch Analysis and Related Approaches, p. 40; Methods and Principles in Medicinal Chemistry, R. Mannhold, P. Krogsgaard-Larsen and H. Timmerman, eds. VCH 1993.
Ghose A.K.; Crippen, G.M. Atomic Physicochemical Parameters for Three-Dimensional Structure-Directed Quantitative Structure-Activity Relationships. I. Partition Coefficients as a Measure of Hydrophobicity. J. Comput. Chem., 1986, 7, 4, 565-577.
Ghose A.K.; Crippen, G.M. Atomic Physicochemical Parameters for Three-Dimensional Structure-Directed Quantitative Structure-Activity Relationships. 2. Modeling Dispersive and Hydrophobic Interactions. J. Chem. Inf. Comput. Sci., 1987, 27, 1, 21-35
Viswanadhan,V.N.;Ghose A.K .; Revankar,G.R. and Robins,R.K. J. Chem. Inf. Comput.Sci, 1989, 29,163.
Padrón, J.A.; Carrasco, R and Pellón, R.F., J. Pharm.Pharmaceut. Sci. Molecular descriptor based on a molar refractivity partition using Randic-type, graph theoretical invariant. (www.ualberta.ca/~csps) 5(3)267-274, 2002.
RIGA Editor, Institute of Organic Synthesis, Latvian Academy of Science, Riga, Latvia, 1991
STATISTICA for WINDOWS, version 4.0, Statsoft, Inc.(1993)
Borea, P. A., Pietogrande, M.C. Biagi,G.L., Guerra, M.C., Barbaro, A.M. and Recanatini, M.; QSAR: Quantitative Structure-Activity Relationships in Drug Design, Alan R. Liss, Inc. New York, pp. 361-364 (1989).
Tamm, I; Folkers, K; Shunk, C.H.; Horofall, F.L.; J. Exp. Med., 1953, 98, 245.
Corresponding Author: Ramon Carrasco Velar, Pharmaceutical Chemistry Center, Ave. 25 y 158 Rpto. Atabey, Playa Aptdo. 16042, La Habana, Cuba. carrasco@cqf.co.cu
Published by the Canadian Society for Pharmaceutical Sciences.
Copyright © 1998 by the Canadian Society for Pharmaceutical Sciences.
http://www.ualberta.ca/~csps