J Pharm Pharmaceut Sci (www.ualberta.ca/~csps) 5(3):258-266, 2002
Molecular descriptor based on a molar refractivity partition using Randic-type graph-theoretical invariant.
J. A. Padrón, R. Carrasco1, R.F.Pellón
Pharmaceutical Chemistry Center, Calle 200 y 21, Atabey, Playa, La Habana, CubaReceived 20 November 2001, Revised 1 October 2002, Accepted 2 October 2002
PDF version
Abstract
PURPOSE: Development of a novel semi-empirical descriptor (MRχ) for molecular modelling. METHOD: The index is based on a molar refractivity partition using Randictype graph-theoretical invariant. RESULTS: This hybrid index describes not only the London dispersive forces in a ligand fragment related to the molar refractivity but also structural features of the molecule It is also applicable in Quantitative Structure-Activity Relationship (QSAR) and Quantitative Structure-Property Relationship (QSPR) studies. CONCLUSIONS: The method is convenient and can discriminate between isomers.
Introduction
In the drug design process, the X-ray tridimensional structure allows evaluation of the the binding energy of several ligands with the receptor and finds the conformations and groups with optimal binding. If the X-ray receptor structure is not known there is the possibility to work on similar protein that posses structural and functional analogy. But often there is no information about the nature of the receptor, hence the efforts must be focused on the structure of the active molecule itself. The binding energy of a ligand with the receptor involves (1): 1) the 3D structure of the biological receptor and its conformational dimensional flexibility; 2) the knowledge of the active site; 3) the conformational behaviour of the ligand; 4) the interaction of the biophase with the ligand and with the receptor; and 5) the interaction of the ligand with the receptor. Each one of these aspects has their own enthalpic-entropic contribution, and the final balance of these factors will determine if the process take place. Subsequently, the researcher is forced correlating the biological response with structural aspects as well as global or partitioned physical-chemical properties of the ligand. These physical-chemical properties represent the different types of molecular forces that are involved in the binding process (1). The first part of the problem is then the identification of the forces (covalent, ionic, hydrophobic, Van der Walls forces) that are involved in the biomolecular interaction, and the second one consists in identifying the chemical-physical properties that can model these forces.
Whereas it is obvious that the geometric and electronic structure of a molecule has to contain the features responsible for physical and chemical properties, it is less obvious that they can be discerned in a simple way. Then, two major types of parameters used in QSAR studies to correlate with biological activity are (2): 1) empirical, which are a measure of physicochemical properties and can be experimentally determined, and 2) non-empirical or topological indices, which are generated from the molecular structure of the compound by counting its fragments, paths, bonds, atoms, etc. which can not be experimentally determined but they encode the chemical structure and are broadly used.
In these work we combine, in a semi-empirical index, the molar refractivity (MR) with topological aspects of the molecules using the Randic graph-theoretical invariant (3). The MR values employed are the atomic refractivity developed by Ghose and Crippen (4-5). The objective of this paper is to demonstrate the possibility of combining a partitioned chemico-physical property with topological algorithm in an hybrid index, and the utility of this index in QSAR and QSPR studies, specifically when the problem involve non-specific chemical interactions.
Molar refractivity and polarizability
The molar refractivity is a constitutive-additive property that is calculated by the Lorenz-Lorentz formula:
where M is the molecular weight, n it is the refraction index and r the density, and its value depends only of the wave longitude of the light used to measure the refraction index. For a radiation of infinite wavelength, the molar refractivity represents the real volume of the molecules. Molar refractivity is related, not only to the volume of the molecules but also to the London dispersive forces that act in the drug-receptor interaction.
According to S. Gladstone (6), the first attempts of making a rational partition of the molar refractivity in the involved electronic groups were A.L. von Steiger in 1921, K. Fajans in 1924 and C. P. Smith in 1925. Nevertheless, the importance of splitting the molar refractivity in their atomic component for QSAR studies guided to three-dimensional molecules, has been demonstrated by Crippen et al. A method for the estimation of molar refractivity, based on the assignment of 22 atomic contributions obtained by classification of each atomic fragment according to the number and nature of the connected atoms to him, was developed by those authors (4-5, 7-8). The reported correlation coefficient between observed and predicted values of the property using the method is 0.999, with standard deviations values of 0.774. This method has been widely used for this property estimation and QSAR studies.
Graph theory. The Randic-type graph theoretical invariant.
Graph theory is a branch of mathematics related to topology and combinatorial problems (9). A large number of topological and topographical indices have been reported by different authors as well as their broad and successful applicability in QSAR and QSPR studies. But the principal problems of its use are related to its physical meaning and the duplication of information among indices of similar definition, commonly expressed by high correlation values between indices (10). On this subject Randic stated (11) that a novel molecular descriptor need to be simple, add more insights to the problem, or to solve a problem that was not explained with alternative schemes, among others that will be discussed later.
Elementary definitions in chemical graph theory
In chemical graph theory, vertices represent atoms and edges represent bonds.
Figure 1: Example of molecular graph.
Then combinations of vertices and edges generate other subgraphs, graphically defined as shown in figure 2.
Figure 2: Examples of different fragments or subgraphs.
Molecular connectivity index
The molecular connectivity index rχ (9) is defined as
and is a generalisation of the χ index for path of order p. The index rχ was modified by Kier and Hall (12-13) by defining subgraphs Gj tree type in the G graph containing edges. To each vertex i of graph G is associated a term σ i (for example σ i =υ i ). After this, to each subgraph Gi with vertices j1,..., jh+1 is calculated the magnitude
The numbers F (σi1,σj(h+1) are then summated on all the subgraphs Gi . To take into account the multiple bonds and heteroatoms, Kier and Hall suggested the employ of σi as,
where Zi is the total number of electrons, Zvi is the number of valence electrons and hi is the hydrogen atoms number bonded to atom i. The connectivity indices obtained by this way are known as valence indices and are represented by (14) hχv . A more detailed explanation of the graph theory and calculation procedures can be found on Molconn-Z 3.50 Manual (15).
The molar refractivity partition index PMRχ
The molar refractivity partition index (MR χ ) using the Randic-type graph-theoretical invariant is defined as follow,
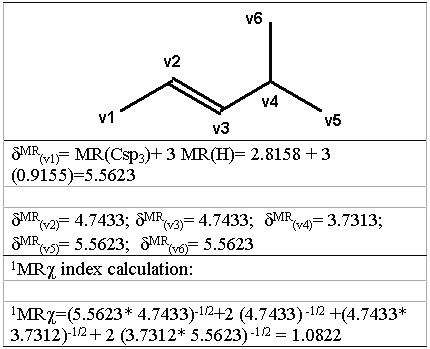
where the sum is all over l adjacent vertices in the graph and σ MR( vi) is the atomic refractivity value of the vi atom, plus the atomic refractivity values of the hydrogens bonded to the vi atom, to include the contribution of hydrogens to the molar refractivity values in the hydrogen-suppressed graph. In figure 3 is shown an example of the calculation technique of the PMRχ index with 4-methyl-2-pentene, where the hydrogen-suppressed graph is also shown. For subgraph of higher orders, the number of the terms in equation 5 is equal to the number of vertices in the subgraph.
Figure 3: Computation of the 1MR χ index for 4-methyl-2- pentene.
In all cases MR χ index calculation involve three steps: a) the molecular structure generation, performed by the RIGA program (16), b) classification of the atom types according to table 1 and c) PMRχc index calculation using software developed in the author's laboratory (17).
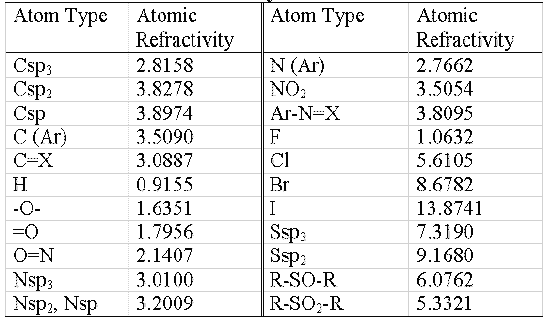
Table 1: Atomic refractivity values
The superscript p and c indicate path order and cluster order, respectively. Paths of order 1 to 6, clusters of order 3 and 4, and combinations of cluster 3 with path order 1 to 3 were calculated. The statistical analysis of the data was carried out using the program STATISTICA v.4.0.
The atomic refractivity values for each atom type are shown in table 1.
Results and discussion
As previously stated, there are desirable properties of topological indices (18). These properties include: direct structural interpretation, good correlation with at least one molecular property, good discrimination of isomers, locally defined, generalizable, linearly independent, simplicity, not based on physical of chemical properties, not trivially related to other indices, efficiency of construction, based on familiar structural concepts, correct size dependence, gradual change with gradual change in structures.
The word topological is emphasized because this 13 criteria are proposed for these type of indices and we postulated that the MRχ index is not a pure topological but mixed index. Then, the criteria #8 will be discharged and others will be discussed in some details to gain insight in the quality of the index. These criteria postulated by Randic are the best guide to analyse any descriptor based on the chemical graph.
The MR χ index has direct structural interpretation in the same extension as other graph-based indices. The topological feature of MRχ takes in to account the nature of the fragment it represents and, with the inclusion of the atomic refractivity of its environment, is possible to analyze the influence of London forces on the corresponding fragment and the relationships with another molecules.
As the MRχ index is based on the Randic algorithm, is easy to understand that it is locally defined in the same way. Equally, it is generalizable to higher order fragments.
The MRχ index is simple and easy to construct. The Randic algorithm is well known. For the calculation of MRχ only is necessary in addition, the identification of each atom with the corresponding atomic refractivity and the sum of the hydrogens to heavy atoms bonded.
The molecular indices based on connectivity matrix are criticised because of the frequently high correlation between them. In this sense, it is advisable to test the duplication of information with other topological indices. The 1MRχ , 1χ , 1χv, 1ε, 1εr, 1Ω, 1ΩQ and 1ΩQC indices were calculated for a 508 compounds sample (19) including hydrocarbons, alcohols, acids, ethers, esters, aldehydes, ketones, amines and halogenated compounds. The correlation matrix between indices was calculated (table 2).
Table 2: Correlation matrix between different indices.
This result shows that, while there is a high correlation values among indices, 1MRχ only has a significant correlation with 1Ω and 1χ , but less than the others. Therefore, the weighting of the vertices in the adyacence matrix with the atomic refractivity values and the calculation of Randic algorithm produce a new hybrid index with a different information contents, related by definition to the molar refractivity values included on its calculation. That is to say, related to London dispersive forces.
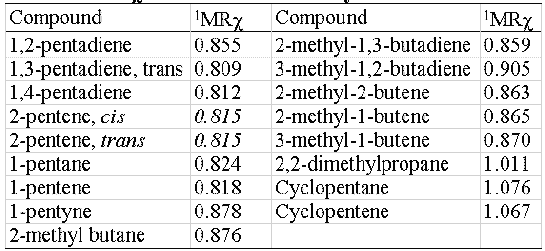
MRχ index shows an acceptable isomer discrimination capability, feature desirable but not indispensable in molecular descriptors. In table 3 the 1MRχ values of a 5-atoms- hydrocarbons set are shown. No cis-trans isomer discrimination can be obtained.
Table 3: 1MRχ values for a 5-atoms-hydrocarbons set.
The index also presents an exact size dependent correlation.
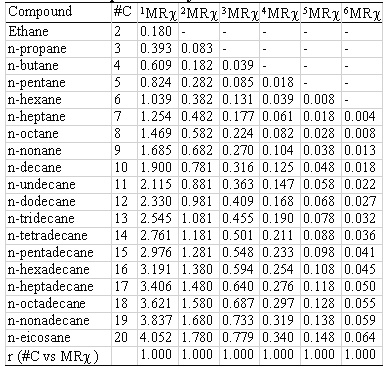
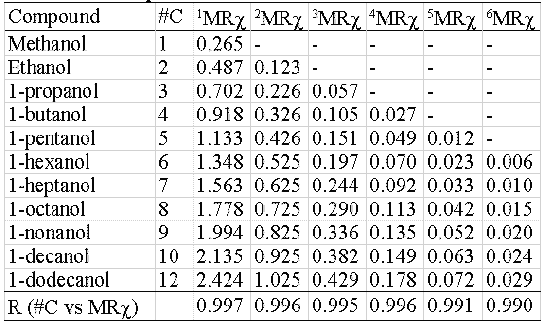
Two homologous series and their correspondent MRχ values of different orders are shown in table 4 (hydrocarbons) and 5 (alcohols). The correlation coefficient between carbon-number and MRχ values is also presented. In all cases the r- values are higher than 0.99 (r@1).
Table 4: Index size dependence. Hydrocarbons.
Table 5: Index size dependence. Alcohols.
Physico-chemical meaning of PMRχ index in qsar studies
The direct interpretation of a molecular property that shows a double meaning like the molar refractivity could be an annoying task, more if it is splitted in fragments. However, these splitting values can be used as a measure of the weight or importance of the analysed fragment on the biological or chemical property. Hence this index is an approach to identify important fragments for the association between the drug and the receptor.
Correlation with the molar refractivity
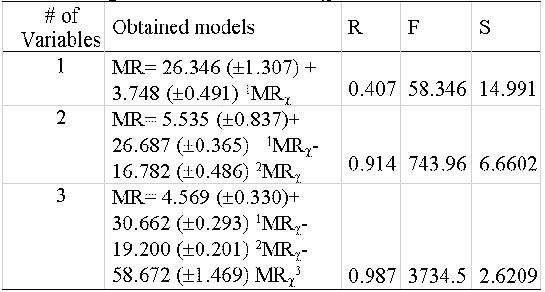
An index like the proposed should be able to reflect the MR by a combination of different subgraphs. That must be true because a high correlation with only one of the subgraphs would imply a trivial relationship with the property. To determine the relationships between PMRχ and MR a heterogeneous sample of 295 compounds (hydrocarbons, alcohols, acids, ethers, esters, aldehydes, ketones, amines and halogenated compounds), was selected. These values were correlated with the MR, incorporating the variables one by one to analyse their weight in the correlation (table 6).
Table 6: Regression models of PMR χ vs MR.
The final model obtained satisfies the consideration that for a study of structure-property relationship it should be obtained correlation coefficients above 0.95. Then, is possible to affirm that a combination of these indexes is related to MR and therefore with the London forces. On the other hand, the relevance of the property fragmentation is evidenced in the improvement of the model (r=0.4, 0.91, and 0.99) with the inclusion of indices of different orders: Path order 1, path order 2 and cluster order 3. Also, others statistical parameters are substantially improved (F and s). Therefore, the proposed hybrid index MRχ is not trivial and it is possible to affirm that it possesses information, not only about the topology of the molecule but also of the dispersive forces expressed by the MR values.
Application of PMRχ index in qspr studies
As a molar refractivity partition, the index shows less applicability on this field than the classical topological indices. Nevertheless, a QSPR study using PMRχ is valid whenever the molar refractivity is related to the studied property. As an example of the applicability of the index, it was correlated with the RM values (20) (R M35% =R M measure using buffer - acetone 65+35; R M40% =R M measure using buffer - acetone 60+40) obtained by thin layer chromatography of 14 isomeric phenol derivatives. Equation for R M35% and R M40% and statistical parameters are shown in table 7.
Table 7: Regression models obtained and reported for predict R M values of 14 isomeric phenol derivatives. r, s and F represent the correlation coefficient, standard deviation of regression, and Fisher ratio respectively.
According to the results the index perform better than other tested indices. This fact must be related to the information content of MR χ index, able to express interactions, not only between the solute and the stationary phase, but as well as the partition coefficient considerate the solute affinity to the phases, the index consider this type of interactions too. The regression analysis show that when the polarity in the mobile phase is decreased, in the model appear a variable of high order (6), with a great negative coefficient value; the order 4 variable disappeared, and is substituted with the order two MRχ , with positive contribution. That means that, when working with the first solvent mixture, the influence of the size of the different fragments is expressed by an index of media size as 4MRχ . This fragment type or subgraph encodes the influence in the association capability of the compounds with the stationary or mobile phase in the conditions above mentioned.
When the polarity is diminished, it can be distinguish as the largest fragments, although shows less occurrences in the chemical structure (less value of the index), are capable of diminish the affinity with the stationary, the mobile or both phases. The MRχ index express the polarizability and the size of the molecules as a function of the considered fragment an its local MR value.
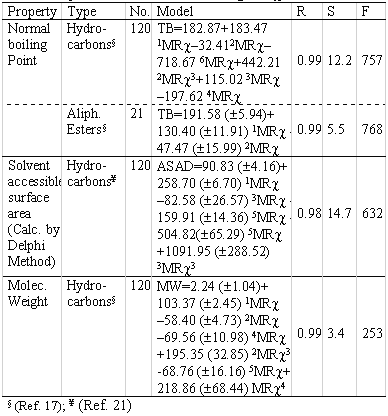
Others QSPR models have been found related to different physicochemical properties during the development of the index. Those models are summarised in Table 8.
Table 8: QSPR models obtained using MR χ index.
The index correlate well with different physico-chemical properties as normal boiling points of hydrocarbons, the molecular weight and an important descriptor related to lipophilicity as the Solvent Accessible Surface Area (SASA). The first two properties are more related to the topological feature of the molecules. In this sense, the correlation can be considered logic, taking into account that the molecular topology is very important for these properties.
In the case of SASA, this consideration is something different because for this property, the polarizability of the molecules determines the capability to associate solvent molecules, not only the topological features. From the table 8 can be see that the hybrid index MRχ , don't correlate in a simple way with the corresponding property. In the regression model always appear two or more variables to underline that different subgraphs or fragments in the molecules have influence in the analysed property.
Application of PMRχ index in qsar studies
Many authors confer an important role to the molar refractivity to model the dispersive forces in biological processes. According to the previously expressed characteristics of the PMRχ index, we consider that it is applicable fundamentally in QSAR studies whenever these forces has a important role in the biological activity. We carried out several QSAR studies in different families previously reported in the literature to test the index capability to represent phenomenons associated to dispersive forces. The results are briefly discussed in the next examples
Cell growth inhibition by 10 1H-isoindoleines
In the model purposed by Lukovits using the Wiener index S he reported r=0.791 and F=13. (22) and in the Estrada's report using the spectral moments μ2ª and μ0b the obtained values were r=0.935, s=0.205 and F=24 (23).
The model raised by MRχ is given by the equation 6
From statistical point of view, the model with MRχ seems to be the best equation of a single variable reported in literature. Although this result is not better than the model obtained by Estrada with the spectral moments, the result strongly suggest that the London forces, together the topology of the molecules, play the principal role in the inhibition of cell growth by 10 1H-isoindoleines. This feature is not taking into account by spectral moments.
Hepatic esterase inhibitory activity of 17 alcohols in sheeps
In 1980 (24) Kier reported several models for this activity using the negentropy index, χ index, molecular weight and log P. The resulting models for these descriptors shows the following r and s values: (r=0.97, s=0.2); (r=0.95,s=0.24); (r=0.94, s=0.27); and (r=0.93, s=0.31) respectively. In 1995 (25) Estrada reported his model using Ω index, with r=0.97 and s=0.19.
The model with MRχ is given by equation 7.
The obtained model seems to be the best equation reported in literature to describe this biological activity of the compound set. Furthermore, the regression model obtained with the MRχ index assess that the activity is due, not only to pure structural aspects or to lipophilicity as given by the precedent models, but also to the dispersive London forces.
Lypoxigenase inhibitory activity of 12 alcohols
In the same work and with the same indices (24), Kier reported several models for this activity. The r and s values were: (r=0.98, s=0.14); (r=0.97, s=0.16); and (r=0.98, s=0.14) for negentropy, χ , molecular weight and log P respectively. On the other hand, Estrada obtained a model using Ω with r=0.99 and s=0.074 (25).
As the knowledge about inflammation is in constant growing, the models reported by Kier and Estrada were employed for comparison purposes only. The regression with the log Po/w tells us about the role (transport) in the activity of this important property. These equations are similar to the ones reported by us. The correlation with the Ω index take into accounts, only structural aspects. This last model is equivalent, from a statistical point of view to the obtained with MRχ . Nevertheless, the calculation of MRχ index doesn't need previous semiempirical calculation as Ω does. The substantial difference between these results is that with MRχ the role of the London forces in the interaction of the molecules is underlined.
Anesthetic effect of 13 barbiturates in mice (AD50)
Basak (26) studied the anesthetic effect of 13 barbiturates in mice with different indices. He employed the Theoretical Information Index (TIC, based in the information theory), two topologic indices (1χ and Wiener index) and log P . He obtained different models with the following results: (r=0.97, s=0.10); (r=0.98, s=0.08); (r=0.97, s=0.10) and (r=0.97, s=0.10), respectively. But the model obtained with MRχ (eq. 8) seems to be the best equation reported in literature to describe the biological activity of this compound set. This improved result suggests that the London forces are involved by molecular fragment in the anesthetic effect of barbiturates in mice.
In all cases the MRχ index was capable to represent how changes in the chemical structure modify the biological activity of the compound set; better or in a similar way than other classical indices. Note that in almost all cases the activity is expressed as the inhibition of a macromolecule function. Therefore is logical to think that a specific interaction between a receptor site and the molecule occurs, and that the proposed index contains the necessary information about the main forces that are involved in the biological activity.
Conclusions
The atomic refractivity values proposed by Crippen et al and the Randic-type graph-theoretical invariant were used to generate a new hybrid molecular descriptor (MRχ ). It outlines the weight of the molar refractivity of fragments of the analysed molecules, in the biological activity or chemical property. Hence, it contain a representation of the dispersive forces involved in the compound macromolecule interaction; and also topological information about the chemical structure of the ligand. Besides, MRχ index has good discrimination of isomers and his calculation is very simple. The proposed index promises to be useful in quantitative structure-activity relationships as well as in quantitative structure-property relationships whenever dispersive forces are involved.
Acknowledgements
This work was supported by grants from the Ministry of Science, Technology and Environment of the Republic of Cuba and the Pharmaceutical Chemistry Center.
One of the authors (RC) wishes to thank Prof. J. Galvez (Valencia, Espana) for the useful discussions and suggestions.
References
Kubinyi, H., QSAR: Hansch Analysis and Related Approaches, pp. 6-13. En: Methods and Principles in Medicinal Chemistry, R. Mannhold, P. Krogsgaard-Larsen y H. Timmerman, Eds. VCH Publishers, Inc., New York, 1993
Ibid. pp.21-55
Randic, M. On Characterization of Molecular Branching, J.Am.Chem.Soc., 97:6609-6615, 1975
Ghose A.K. and Crippen, G.M., Atomic Physicochemical Parameters for Three-Dimensional Structure-Directed Quantitative Structure-Activity Relationships I. Partition coefficients as a Measure of hydrophobicity, J.Comput.Chem., 7:565-577, 1986, and references therein
Ghose A.K. and Crippen, G.M., Atomic Physicochemical Parameters for Three-Dimensional Structure-Directed Quantitative Structure-Activity Relationships 2. Modeling Dispersive and Hydrophobic Interactions J.Comput.Chem., 27:21-35, 1987
Glasstone, S. Thermodynamics for Chemists. La Habana, Instituto Cubano del Libro, 1969
Ghose A.K.; Pritchett, A; Crippen, G.M. Atomic Physicochemical Parameters for Three-Dimensional Structure-Directed Quantitative Structure-Activity Relationships 3. J.Comput.Chem., 9:80-90, 1988
Viswanadhan,V.N.; Ghose A.K.; Revankar, G.R. and Robins, R.K., Atomic Physicochemical Parameters for Three-Dimensional Structure-Directed quantitative Structure-Activity Relationships 4. Additional Parameters for Hydrophobic and Dispersive Interactions and Their Application for an Automated Superposition of Certain Naturally Occurring Nucleoside Antibiotics, J.Chem.Inf.Comput.Sci, 29:163-172, 1989
Harary, F., Graph Theory, Addison-Wesley, Reading MA, 1969
Basak, S.C.; Magnuson, V.R.; Niemi, G.J.; Regal, R.R.; Veith, G.D. Topological Indices: Their Nature, Mutual Relatedness, and Applications, Math. Model, 8:300-305, 1987
Randic, M.; Hansen, P.J.; Jurs, P.C., Search for Useful Graph theoretical Invariants of Molecular Structure J.Chem.Inf. Comput.Sci., 28:60-68, 1988.
Kier L.B. and Hall L.H., The Nature of Structure-Activity Relationships and their Relation to Molecular Connectivity Eur. J. Med. Chem. Chim. Ther., 12, 307-314, 1977
Kier L.B. and Hall L.H., General Definition of Valence Delta Values for Molecular Connectivity J.Pharmacol.Sci., 72:1170-1181, 1983
Kier L.B. and Hall L.H., Derivation and Significance of Valence Molecular Connectivity, J.Pharm.Sci. 70:583-589, 1981
Molconn-Z 3.50 Manual; www.eslc.vabiotech.com/ molconn/manuals/350/chapone.html
Riga Editor, Institute of Organic Synthesis, Latvian Academy of Science, Riga, Latvia 1990
Padrón, J.A. and Carrasco, R.; La Habana, (2002). Program for the calculation of MRc Index. It will be submitted on request.
Randic M., Generalized Molecular Descriptors, J.Math.Chem., 7:155-168, 1991
Reid, R. C.; Prausnitz, J. M y Poling, B. E.; "The Properties of Gases and Liquids", McGraw-Hill Book Co., New York, 4th Ed. 1987
Pika, A., Topological Indices and RM Values of Isomeric Phenol Derivatives in Structure-Biological Activity Studies: Part V!., J. Planar Chromatogr. 8:51-62, 1995
Padrón, J.A.; Carrasco, R.; Marrero, J. and Pardillo, E.; Topologic and Topographic Indices for the Prediction of Solvent Accesible Surface Area of hydrocarbons, Revista CENIC Ciencias Químicas, 32:99-103, 2001 (Spanish)
Lukovits I., Decomosition of the Wiener topological Index. Application to Drug-Receptor Interactions, J.Chem.Soc.Perkin Trans. II, 1667-1671, 1988
Estrada E., Three-Dimensional Molecular Descriptors Based on Electron Charge Density Weighted Graphs J.Chem.Inf.Comput.Sci, 35:708-713, 1995
Richard, A.J. and Kier L. B., Structure-activity analysis of hydrazide monoamine oxidase inhibitors using molecular connectivity, J. Pharm. Sci. 69:497-502, 1980
Estrada E. Doctoral Thesis, Universidad Central de Las Villas, Cuba. 1995
Basak S.C.; Monsrud, L.J.; Rosen, M.E.; Frane, C.M. and Magnuson, V.R., A Comparative Study of Lipophilicity and Topological Indices in Biological Correlation, Acta Pharm. Jugosl. 36:81-95, 1986
Corresponding Author: R. Carrasco, Pharmaceutical Chemisry Center, Calle 200 y 21, Atabey, Playa, La Habana, Cuba. carrasco@cqf.cu
Published by the Canadian Society for Pharmaceutical Sciences.
Copyright © 1998 by the Canadian Society for Pharmaceutical Sciences.
http://www.ualberta.ca/~csps