J Pharm Pharmaceut Sci (www.ualberta.ca/~csps) 5(2):190-198, 2002
Statistical analysis of tablet breakability methods
Lieven Van Vooren, Bart De Spiegeleer1
Health Engineering and Assurance (HEA), Gent, BelgiumThomas Thonissen, Philippe Joye, Joost Van Durme, Guido Slegers
Faculty of Pharmaceutical Sciences, Ghent University (RUG), Gent, BelgiumReceived 4 February, 2002, Revised 18 June 2002, Accepted 24 June 2002
PDF version
Abstract
Purpose: Using a model tablet, the influence of breakability methodology on mass uniformity of half- and quarter-tablets as well as the comparison of different data acquisition and evaluation approaches were investigated. Moreover, different breakability evaluation criteria were compared based upon distribution as well as distribution-free models.
Methods: A cross-scored tablet, i.e. having two break-marks, was broken by different methods by different persons, and the masses determined for the whole (unbroken) tablets, the half-tablets and quarter-tablets.
Results: Beside the possible interaction between the methodology and the person breaking the tablets, the major factor significantly influencing the mass uniformity of broken tablets is the breakability methodology. The best results, i.e. smallest loss and smallest variability, are obtained when the breaking force applied by the thumbs is directed towards the score side of the tablet, i.e. by "opening" the score. Using our model tablet, significant differences between the different evaluation criteria are observed, with the USP/NF approach being best in line with the detailed analysis of all broken tablets.
Conclusions: Assuming that for this model tablet the variance is a linear function of the break-line length, the standard deviation of quarter-tablets is theoretically calculated to be 0.87 times the standard deviation of the half-tablets. As the absolute standard deviation, expressed in mass units, will thus remain approximately identical, the relative standard deviation will nearly double as the mean mass of the quarter-tablets will be half of the mean mass of the half-tablets. This was experimentally confirmed.
Introduction
Tablets with single or multiple score lines allow the administration of a proportion of the tablet. In general, pharmacopoeial mass or weight uniformity compliance criteria (1-2) do not consider the specific broken-tablet situation, and consequently the general unit-dose criteria are generally believed to be applicable to half-tablets and quarter-tablets as well. Only recently, there is the explicit addition that the subdivided parts of a tablet should indeed also comply with the content or mass uniformity requirements (3).
In the literature, a number of alternative criteria (4-7) have been proposed, generally allowing mass variations of broken tablets to be higher than intact tablets. Only little information in the literature is available describing standardised breakability test methods (6). The use of quarter-tablets is hardly investigated because it is expected that their variability is significantly higher than that of half-tablets (4, 7). A recent overview article summarises the scarce literature data available (8).
The aim of this study is to investigate the influence of breakability methodology on mass uniformity of half- and quarter tablets, as well as to compare different data acquisitions and evaluation approaches, using a discriminative model tablet
Materials and Methods
Drug dosage form tested
The tablets applied for this study are cross-scored on one side, weighing 400 mg and containing 22% m/m drug substance. The tablets are intended for veterinary use in the treatment of dogs. The large weight variety in the target animal species justifies the requirement of a cross-scored tablet for the intended purpose.
The tablet is manufactured by wet granulation followed by compression. The tablet consists of microcrystalline cellulose, sorbitol and dried yeast lysate as main excipients. Preliminary data showed that this tablet was suitable as a discriminative model tablet relative to breakability.
The tablets are flat and round, with a diameter of 11 mm and a height of 3.7 mm. Both score lines (break-marks) applied in this cross-score have the following characteristics (9): W (width) = 0.88 mm, D (depth) = 0.42 mm, q = 45° and R (engraving cut radius) = 0.05 mm.
Breakability test methods
In a preliminary experiment, three persons experimented with diverse breakability test methods using the selected tablet. Some methods (e.g. pressing, use of support material) were not feasible with the flat test-tablets, or were considered too artificial compared to the real-life situation. The following five breakability test methods were retained:
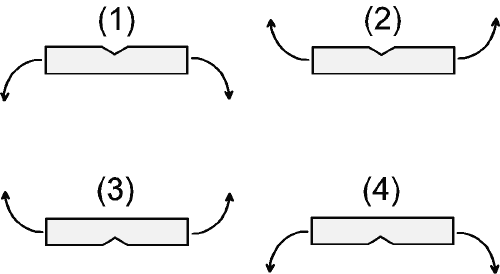
Hold the tablet between the thumb and the index finger of each hand on either side of the score line, with the score line facing upwards and without using the nail. Separate into two halves by breaking open the tablet at the score line side (legend: score up - break).
Hold the tablet between the thumb and the index finger of each hand on either side of the score line, with the score line facing upwards and without using the nail. Separate into two halves by breaking open the tablet opposite the score line side (legend: score up - fold).
Hold the tablet between the thumb and the index finger of each hand on either side of the score line, with the score line facing downwards and without using the nail. Separate into two halves by breaking open the tablet at the score line side (legend: score down - break).
Hold the tablet between the thumb and the index finger of each hand on either side of the score line, with the score line facing downwards and without using the nail. Separate into two halves by breaking open the tablet opposite the score line side (legend: score down - fold).
Place the tablet horizontally on the table, with the score line facing upwards, and place a kitchen knife on the score line. Put pressure on the knife with the free hand, until the tablet breaks (legend: score up - knife).
The first four breakability methods are illustrated in Figure 1. Method 1 is considered the most natural way for breaking tablets.
The five methods described above are applicable to break tablets into half-tablets, as well as to break half-tablets into quarter-tablets.
Figure 1: Visualisation of the first four breakability methods
Data acquisition
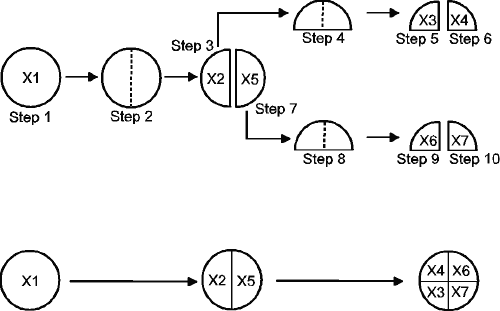
The study test protocol is visualised in Figure 2 and consists of 3 breaking steps (i.e. break tablet into 2 half-tablets, and subsequently break both half-tablets into quarter-tablets) and 7 weighing steps (in mg ± 0.1 mg). The seven weights are coded from X1 to X7 and are obtained in the following sequence: tablet weight X1, left half-tablet weight X2, left quarter-tablet weight X3, right quarter-tablet weight X4, right half-tablet weight X5, left quarter-tablet weight X6, right quarter-tablet weight X7. Three right-handed persons executed the protocol with each of the five test methods described above, using 30 tablets per method.
Figure 2: Visualisation of the different steps in the test protocol and the corresponding physical orientation of half- and quarter-tablets
This elaborated set-up contains all possible weight information and allows detailed investigations of all possible relationships such as left-right differences, half-to-quarter interactions, but is not feasible for routine purposes. The following two more practical and routine data acquisition methods described in the literature were evaluated with the collected dataset.
A. Systematic data acquisition approach (5-6)
Only one half-tablet is retained per tablet, taking alternately the right or the left half-tablet. Similarly, only one quarter-tablet is retained per tablet, taking alternately one of the four quadrants. The retained half-tablets or quarter-tablets are weighed individually.
B. Alternative data acquisition approach using extremes (7)
A representative sample of 10 tablets is taken and tablets are individually weighed. Tablets are broken into half-tablets and further into quarter-tablets, if required. The obtained half- or quarter-tablets are individually weighed. For each tablet, the weight of the lightest half- or quarter-tablet is pointed out. The weight of the overall lightest half- or quarter-tablet (OL) is noted. Finally, the following is calculated:
The half- or quarter-value of the average weight of the 10 tablets (A1)
The average weight of the obtained 20 half- or 40 quarter-tablets (A2)
The average weight of the pointed out 10 lightest half- or quarter-tablets (A3)
Evaluation criteria
A. Two pharmacopoeial criteria (1-2)
The uniformity of mass for tablets complies with the requirements of the Ph. Eur., if the weight of 20 tablets complies with the following:
no more than 2 tablets are outside the average weight ± d%;
no tablets are outside the average weight ± 2xd%.
For units over 80 mg and below 250 mg, d = 7.5 and for units of 250 mg or more, d = 5.
The uniformity of dosage units (respectively weight variation and content uniformity) described in the USP/NF is based on the weight combined with the assay of 10 dosage units. Since only the weight of units are considered in this study, compliance with the USP requirements sensu strictu cannot be demonstrated as such. Consequently, the results should be carefully interpreted, with the assumption of a homogeneous distribution of the active drug substance in the tablets.
The content uniformity for tablets complies with the requirements of the USP, if the assay of 10 tablets complies with the following:
all 10 units are within 85 - 115 % LC (label claim) and,
relative standard deviation (RSD) < 6 %
or in case these conditions are not met, an extra 20 units are required, and
B. Three non-pharmacopoeial alternative criteria (4-7)
The first criterion has been proposed by a French committee (5-6) and is based on the coefficient of variation of the weight of half-tablets or quarter-tablets. Twenty retained half- or quarter-tablets are weighed individually and the RSD is calculated. If the RSD is less than or equal to 10%, it may be concluded that the breakability is good. Otherwise, the test is repeated with 20 other tablets and the RSD is likewise calculated on the 40 half- or quarter-tablets retained during the two samples. The breakability may be considered satisfactory only if the new RSD is less than or equal to 10%.
The second proposed Danish criterion (4) is deducted from the Ph. Eur. mass uniformity criterion, but with the allowance of a mass variation of half-tablets (or quarter-tablets) which is twice the variation allowed for intact tablets. Accordingly, the mass of part-of-tablets complies with this criterion if the weight of 20 tablets complies with the following:
For units over 80 mg and below 250 mg, d = 15 and for units of 250 mg or more, d = 10.
The third criterion for acceptance of secability (7) is met, if the following conditions are fulfilled using 10 tablets (see 'alternative data acquisition approach using extremes' in the previous section):
If one unit is outside the third condition, but above 0.75 x A2, the test is repeated on 20 additional tablets. The requirements are met if no more than one unit of the 30 lowest units is below 0.80 x A2 and above 0.75 x A2.
Data analysis
Excel® was used for the data preparation and data processing. Statistical analyses were performed with SPSS® 9.0. Data exploration was performed with box-and-whisker plots, in which the box percentile limits are respectively 25% and 75%. Outlier values (symbol °) and extreme values (symbol *) are defined respectively as deviating more than 1.5 and 3 times the box length starting from the box boundaries. The lower and upper whiskers are defined as respectively the lowest and highest non-outlier values. Mixed model ANOVA analyses were obtained with the General Linear Model (GLM) procedure in SPSS® 9.0. For all statistical tests, a critical significance level a = 0.05 was chosen
Results
Analysis of breaking losses
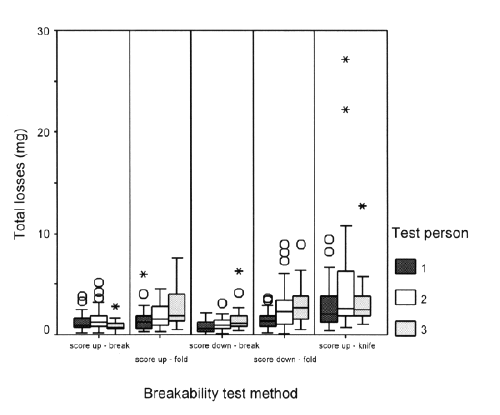
Summarizing box plots shown in Figure 3 present the cumulative or total losses (i.e. loss of 3 successive breakings per tablet) per breakability test method and per operator. .
Figure 3: Box plots of cumulative losses (n=90 per test method)
Further, a tabular overview of the percentage loss (mean, RSD and max.) at each breaking step and per breakability test method is given in Table 1.
Table 1: Breakability losses obtained from breaking tablets into half-tablets and into quarter-tablets for 5 breakability test methods (expressed as % of tablet weight)
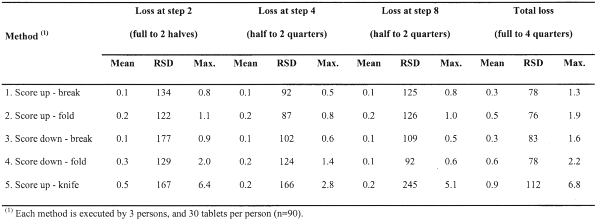
The test method 5 (i.e. using knife) clearly exhibits the highest mean particle losses with the highest variability, including some extreme values such as 6.8% loss for 1 particular tablet. Investigating the operators, it became apparent that by using a knife to break the tablets, visible small pieces of the tablet were sometimes obtained, explaining the extreme loss values. The lowest mean loss per tablet (i.e. 0.3%) was obtained with methods 1 and 3. Consequently, the maximal observed loss per tablet was also lowest for methods 1 and 3, which was in both cases less than 1.6%.
The loss data is modelled as log-normally distributed (Kolmogorov-Smirnov tests), and therefore a log transformation was applied to the data prior to a mixed model ANOVA analysis (method = fixed factor; person = random factor). The interpretation of the main effects (excl. interaction effect) indicates an insignificant person dependency (p = 0.06), although marginally. However, a strong method dependency was found (p = 0.002).
Multiple post-hoc comparison of mean total loss for the 5 methods (Duncan test) resulted in the following three homogeneous subsets, significantly different from each other: 5; (4, 2); (1, 3).
Therefore, it is concluded that the visibility of the score line (score line up versus score line down) is not a critical factor to minimise losses, however, that the direction of the breaking forces towards the score (break open versus fold up) is the determining factor to minimise losses. The score should be "opened" to obtain the best result.
Half-tablets and quarter-tablets weight variability investigation
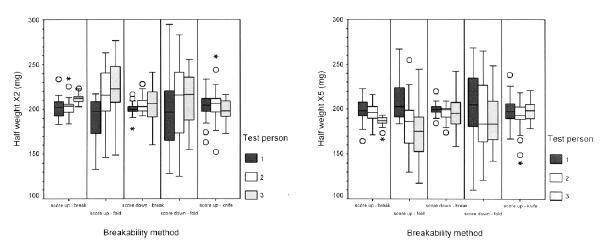
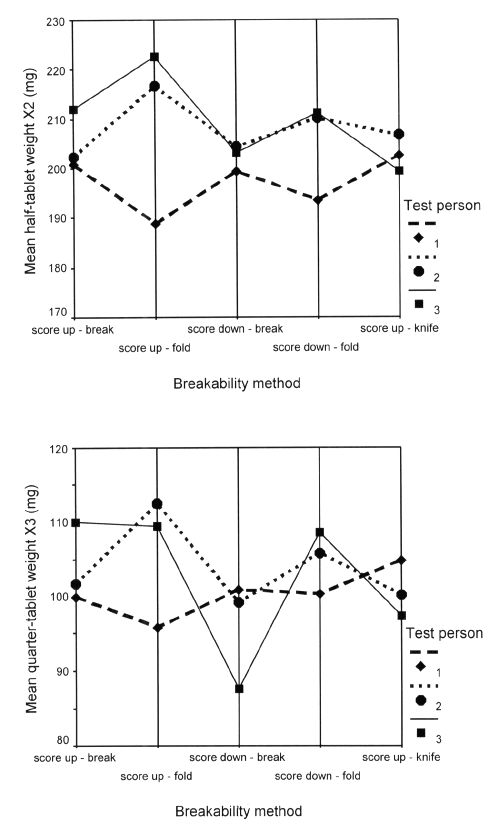
The overall mean tablet weight (X1) was 400.1 mg with a standard deviation of 3.6 mg (n = 450). Explorative clustered box plots of the weight of half-tablets (X2, X5) and quarter-tablets (X3, X4, X6, X7) for the 5 test methods and 3 persons are shown in Figure 4.
Figure 4: Box plots with weights of tablets (X1), half-tablets (X2, X5) and quarter-tablets (X3, X4, X6 and X7) for 5 breakability test methods and 3 persons (n=30 per test method and per person)
Tablet, half-tablet and quarter-tablet weight are modelled as normally distributed (Kolmogorov-Smirnov tests) within each method and person combination.
Mixed model ANOVA analysis on response variables X2 to X7 (method = fixed factor; person = random factor) revealed significant interactions method person, as exemplified with interaction plots for X2 (p = 0.001) and X3 (p < 0.001) in Figure 5.
Figure 5: Method person interaction plots of half-tablet weights X2 (top graph) and quarter-tablet weights X3 (bottom graph)
The further approach consisted in variance component analysis per method. For X2 to X7, the total variability within each method was calculated and split into person variability and residual variability.
The variance estimations of X2 and X5 were pooled to obtain "half-tablet" variance components, and similarly the variance estimations of X3, X4, X6 and X7 were pooled to obtain "quarter-tablet" variance components. For each variance estimate, a 95% confidence interval was calculated using a c2 distribution.
A graphical presentation of the results is given in Figure 6.
Figure 6: Variance components 'person' and 'residual' (expressed as standard deviations in mg including the 95% confidence interval) of respectively half-tablets weight (top graph) and quarter-tablets (bottom graph) for the 5 tested breakability test methods
For both the half-tablets and quarter-tablets, methods 2 and 4 (fold score) exhibit the highest variability (person and/or residual) and are therefore considered not reproducible.
The half-tablet variability of these methods is, however, much higher than their corresponding quarter-tablet variability, which would not be expected at first sight. The relationship between half-tablet and quarter-tablet variability is further investigated in this paper.
For the half-tablets, method 1 has the lowest residual variance, whereas methods 3 and 5 exhibit the lowest person variability. The use of a knife as cutting tool makes this method less dependent on the operator. The 95% confidence intervals on the person variability's are rather large due to the low number of degrees of freedom (only 3 persons) compared to the smaller confidence intervals of the residual variability (30 tablets per person).
The total quarter-tablet variability is lowest for methods 1 and 5. The quarter-tablet person variability is comparable to the half-tablet situation. The quarter-tablet variability of method 3 is significantly higher than those of methods 1 and 5. Within the 3 acceptable methods (1, 3 and 5), the following reproducibility ranking is made (best to worse): method 1 (lowest half-tablet variability), method 5 (low quarter-tablet variability) and method 3. When combining these findings with the results of the previous section (high losses for method 5), methods 1 and 3 are the preferred methods to obtain reproducible breakings.
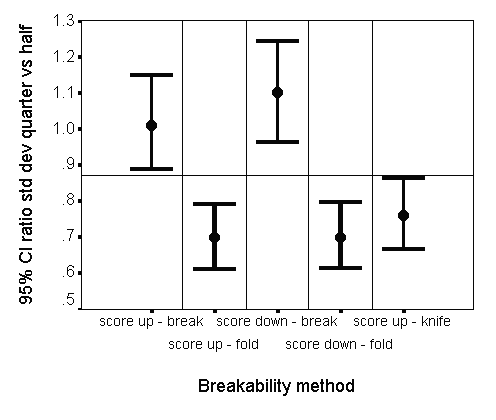
The relationship between the half-tablet variability and quarter-tablet variability was further investigated by calculating the ratio of standard deviation of quarter-tablets versus the standard deviation of half-tablets, for each method. A 95% confidence interval was constructed using an F-distribution. The results are graphically presented per method in Figure 7.
Figure 7: Ratio of standard deviation of quarter-tablet weights versus standard deviation of the corresponding half-tablet weights for 5 breakability methods and comparison with hypothetical calculated value 0.87
From Figure 7 it is noticed that the quarter-tablet variability (expressed as standard deviation) slightly increases for methods 1 and 3 compared to the corresponding half-tablet variability, whereas it decreases for the other methods. This phenomenon was further explored by testing the hypothesis that the variability of part-of-tablets (expressed as variance) is a linear function of the length of the score (i.e. the longer the score, the higher the variability of the corresponding part-of-tablet's weight).
If the variabilities of tablets, half-tablets and quarter-tablets are respectively called
,
and
, then the following mathematical relationships exists:
(1)
(2)
With
: Intrinsic variability of half-tablets inherited from tablets, with hence half the standard deviation of the tablets' standard deviation.
: Additional variability due to breaking a tablet into half-tablets.
: Intrinsic variability of quarter-tablets inherited from half-tablets.
: Additional variability due to breaking a half-tablet into quarter-tablets.
Specifically for the tablets used in this study, the tablet variability
is contributing only very little (i.e. always less than 3%) in the half-tablet variability
, therefore the tablet variability
is not considered in the further calculations. Together with the above hypothesis (i.e.
is half of
because the half-tablet score length is half of the tablet score length), equations (1) and (2) can be combined to give the following relationship between
and
:
(3)
From equation (3), the theoretical expected ratio of quarter-tablet to half-tablet variability, expressed as standard deviation, is 0.87. The overall experimental results are in-line with this theoretical value. Consequently, it may be concluded that the variability of broken tablets is mainly determined by the half-tablet variability, and that breaking half-tablets into quarter-tablets does not imply that the variability increases. However, if relative standard deviations are considered, the RSD of quarter-tablets is around twice the variability of half-tablets.
Breaking symmetry investigation
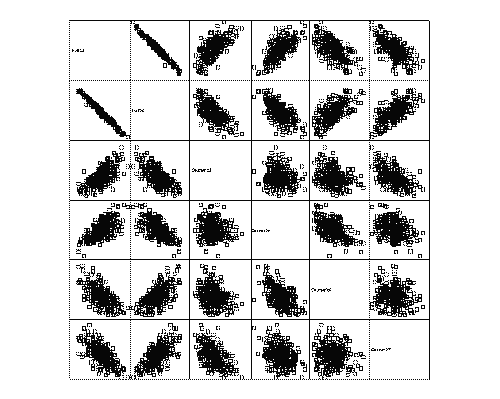
In this section, the relationships between 2 halves (left X2 versus right X5) originating from the same tablet, and 2 quarters (left X3 versus right X4; and left X6 versus right X7) originating from the same half-tablet are investigated in more detail. By comparison of left and right data, the breaking symmetry is assessed. An explorative matrix scatter plot is given in Figure 8. A very significant negative correlation exists between 2 half-tablet weights X2 and X5. Further, a strong positive correlation is observed between the weight of half-tablets and the weight of both resulting quarter-tablets (e.g. X2 versus X3 and X4). The negative correlation between the weights of 2 quarter-tablets originating from the same half-tablet is not very pronounced any more, however, still significant (p = 0.001 and p = 0.012 for both sets of quarter-tablets respectively).
Figure 8: Matrix scatter plot with half-tablets and quarter-tablet weights
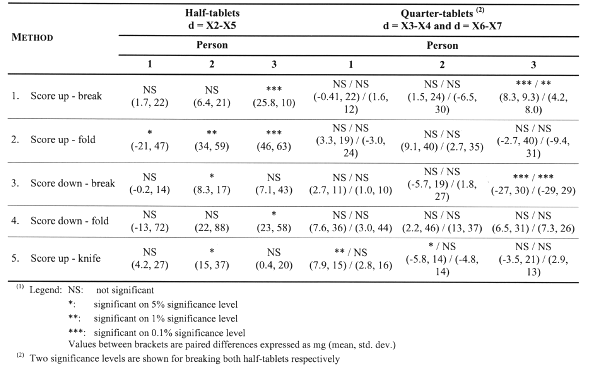
The division symmetry was further investigated with paired t-tests between the left- and right-hand data, for half-tablets and quarter-tablets respectively. Comparisons are performed for each method and within each person, for each of the 3 breakings per tablet. The results are given in Table 2.
Table 2: Division symmetry investigation (i.e. left versus right side) of respectively half-tablets from tablets and quarter-tablets from half-tablets using paired t-tests
The results indicate a personal factor in obtaining symmetrical breakings. For example, person 1 obtains symmetrical halves with each of the 5 methods, whereas person 3 is unable to obtain symmetrical halves with methods 1, 2 and 4. Furthermore, the data shows a clear method preference within persons. For example, person 2 performs well with methods 1 and 4 (for both half- and quarter-tablets), whereas the same methods fail for person 3. Apart from methods 2 and 4 (very high variability, difficult to find significant differences), methods 1, 3 and 5 perform similar to obtain symmetrical part-of-tablets.
From a practical point of view, the negative correlation between part-of-tablet weights within tablets (originating from asymmetrical breakings) can be interpreted as being positive from a clinical point of view because during consecutive treatment of an individual, deviations from the target dose (i.e. due to variation of part-of-tablet weights) will be symmetrically spread out throughout the treatment. Moreover, alternative dosage schemes without breaking tablets (e.g. longer in-between times of two consecutive dosages; or alternatively take in 1 or 2 units per dosage) are less efficient or less appropriate.
Simulation of breakability routine test procedures
The weight uniformity of dosage units (i.e. tablets, half-tablets and quarter-tablets) was assessed using 2 pharmacopoeial and 3 alternative compliance criteria. The weight of complete tablets complied with each of the criteria, and is therefore not discussed in the remainder of this section. For each method and person combination, the compliances for half-tablets and quarter-tablets were determined. Summarising frequency tables with the results are given in Table 3.
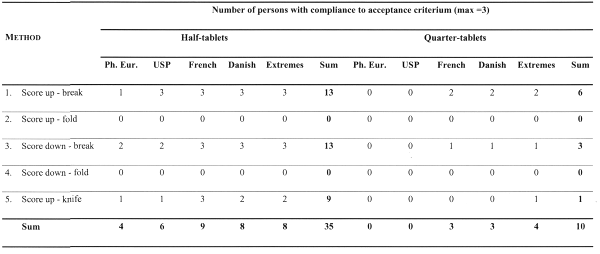
Table 3: Frequency tables of compliance to 5 possible acceptance criteria (2 pharmacopoeial and 3 alternative) for half-tablets and quarter-tablets using 5 breakability test methods (total per cell = 3 persons)
The results in Table 3 confirm that methods 2 and 4 are not reproducible, because all compliance criteria on half- and quarter-tablets failed for both methods.
The preferred methods 1 and 3 comply best with the investigated criteria on both half- and quarter-tablets. Method 5 gives intermediate results.
The alternative compliance criteria are less stringent than both pharmacopoeial criteria (1-2) because they particularly consider the broken-tablet situation. In general, the alternative compliance criteria behave very similar. It is noted that a full comparison of the last criterion (extremes) with the other criteria is sensu strictu very difficult because it is linked to the data acquisition approach B (alternative using extremes), whereas the other criteria were tested with the systematic data acquisition approach A.
Despite that, the variability of quarter-tablets (expressed as variance or standard deviation) is comparable to the half-tablet variability, the compliance criteria generally fail on the quarter-tablets, whereas they comply in many cases on half-tablets. An explanation for this can be found in the relativity of the conditions to be fulfilled (e.g. the use of percentages instead of absolute values), which is the case for all criteria. A proposed alternative criterion approach, which would be applicable for particularly broken-tablets, consists in the use of absolute mass criteria instead of percentage criteria. Moreover, while the scarce literature neglects giving information on cross-scored tablets, it is clear that in certain situations, this is the only viable option, e.g. in veterinary medicine, where otherwise too many marketed dosage strengths will enhance the misuse of the appropriate dosage strength tablets. Therefore, the criteria are to be interpreted in function of the proposed posology, indications and dose-response curve of the drug, i.e. very similar to current approaches in residual solvents and impurity limits settings where several drug-specific situational options are available.
Discussion
The purpose of this investigation was to study the influence of breakability methodology on mass uniformity of half- and quarter- tablets as well as to compare different data acquisition and evaluation approaches. The secondary purpose was to determine the possible relationship between the variabilities observed for the half-tablets with the variabilities of the quarter-tablets.
Using a discriminative model tablet, it has been demonstrated that beside the possible interaction between the methodology and the person breaking the tablets, the major factor significantly influencing the mass uniformity of broken tablets is the breakability methodology. The best results, i.e. lowest loss and lowest variability, are obtained when the breaking force applied by the thumbs is directed towards the score side of the tablet, i.e. by "opening" the score, independent of score line orientation (upwards versus downwards). The other methods, incl. using a knife, gave rise to higher variability and greater loss of particles.
Specific systems for the acquisition of data of the broken tablets were shown not to be of major relevance: an appropriate, at random data acquisition gives similar results to proposed systematic data acquisition approaches.
Different evaluation criteria were compared, based upon distribution as well as distribution-free models, and including pharmacopoeial monographs for unit dosages (1-2), national (France and Denmark) and literature approaches. Using our discriminative model tablet, significant differences between the different evaluation criteria are observed, with the USP/NF approach being best in line with the detailed analysis of all broken tablets.
There exists a strong correlation between the variability of half-tablets and of quarter-tablets. Assuming that for this model tablet the variance is a linear function of the break-line length, the standard deviation of quarter-tablets is calculated to be 0.87 times the standard deviation of the half-tablets. As the absolute standard deviation, expressed in mass units, will thus remain approximately identical, the relative standard deviation will nearly double as the mean mass of the quarter-tablets will be half of the mean mass of the half-tablets. This was experimentally confirmed.
Acknowledgements
The authors would like to thank D. Diels, M. Eyers, H. Steyaert, D. Thoné, K. Van Halewyck and K. Vlaminck for the stimulating discussions and for the provision of tablet samples
References
European Pharmacopoeia. 2001, 3rd edition.
European Pharmacopoeia 2002, 4th edition, addendum April 2002.
Kristensen, H.G., Jørgensen, G.H., and J. Møller-Sonnergaard, J., Mass uniformity of tablets broken by hand. Pharmeuropa, 7:298-302, 1995.
Arnold, J.C., Bon, R., Catterini, A.M., Debrock, C., Gachon, M., Papin, J.P., Russotto, R., Terracol, D., Trottmann, D., Divisibility of tablets. Report of a SfStP committee. S.T.P. Pharma pratique, 5:499-500, 1989.
Moulin, G. and Mourot, D., Tablet divisibility - draft guideline. Ministry of agriculture and forestry, National centre for veterinary and dietary studies. Veterinary medications laboratory, Fougeres, France, pp 2, 1990.
Kister, G., Catterini, A.M., Chanal, J., Jeantet, A., and Ribes, M., De la qualité des comprimés sécables - 1. Essai d'uniformité de poids. Sci. Techn. Pharm., 8:369-378, 1979.
Vaes L.P.J, Frijlink H.W. and Barends D.M., The breaking of scored tablets prior to the Ph.Eur. test. Pharmeuropa, 14: 317-319, 2002.
Loeffler, G.F., Pharmaceutical Tablet Compression Tooling: Lieberman, L.A. and Lachman, L. (Eds.), Pharmaceutical Dosage Forms: Tablets. Marcel Dekker, INC, New York, NY, pp. 451-484, 1981.
Corresponding Author: Bart De Spiegeleer, Health Engineering and Assurance (HEA), Keizer Karelstraat 228, 9000 Gent, Belgium, hea@hea.be
Published by the Canadian Society for Pharmaceutical Sciences.
Copyright © 1998 by the Canadian Society for Pharmaceutical Sciences.
http://www.ualberta.ca/~csps