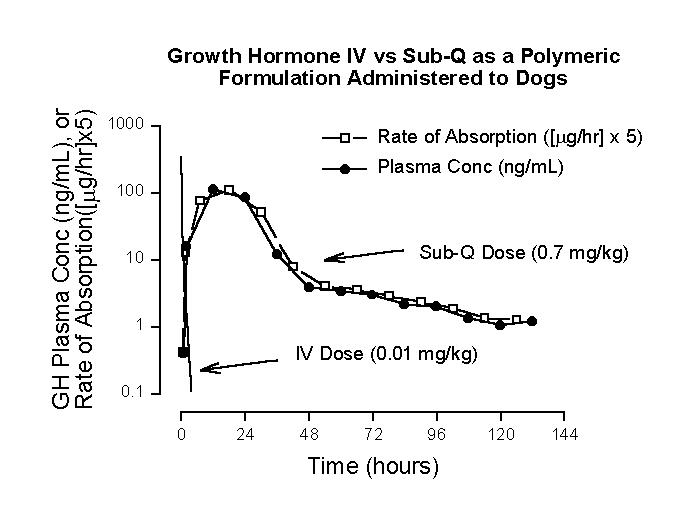
Pharmacokinetics Tricks and Traps: Flip-Flop Models Received manuscript September 1st, 1998; Reviewed September 9th, 1998; Accepted October 23rd, 1998. Harold Boxenbaum1, In the analysis of extra-vascular plasma concentration-time profiles, the disentanglement of influences from disposition and absorption rate influences is often challenging. This can be particularly true when absorption is considerably slower than disposition, that is, in a "flip-flop" system. The purpose of this communication is to define a pharmacokinetic flip-flop system (in a linear system) and characterize some of its properties. The well-known Wagner-Nelson equation (1) characterizing drug absorption in the presence of monoexponential disposition can be rearranged as follows: where Vz is the terminal exponential volume of distribution, K is the terminal disposition rate constant once drug absorption is complete (best determined from IV dosing), C is the plasma concentration at time t and D C is the change in plasma concentration over the time interval D t. In Eq. 1, it is best to utilize C at the time corresponding to the midpoint of (D C/D t). In those situations where KC >> (D C/D t), which serves as a definition of a pharmacokinetic "flip-flop" system, Equation 1 simplifies to:
where (V z)(K) is clearance (CL). Equation 2 indicates that under these conditions, rate of absorption approximates rate of elimination. When this is observed, which can exist during many or most segments of a plasma concentration-time profile, regardless of complexity, the pharmacokinetic profile is in a state of "flip-flop," viz., rate of absorption approximates rate of elimination. In a simplified sense, a "flip-flop" exists when rate of absorption is the rate-limiting step in the sequential/parallel processes of drug absorption, distribution and elimination. The "trap" commonly fallen into is that the terminal exponential phase half-life following extra-vascular dosing is mistakenly thought to exemplify terminal drug disposition, when in fact it characterizes terminal exponential drug absorption half-life. The "trick" that can be applied is simply to recognize that in a "flip-flop" model, the plasma concentration-time profile tends to closely parallel rate of absorption. This provides a simple and effective way to visualize the shape of the rate of absorption profile, without the necessity of deconvolution, e.g., Wagner’s modification of the Loo-Riegelman equation (2).Figure 1. Recombinant human growth hormone (GH) mean semilogarithmic plasma concentration-time profiles (3) following: an intravenous bolus injection of 0.2 mg/kg doses to 4 dogs (theoretical profile based on mean parameters from biexponential curve-fits); and a profile following subcutaneous administration of 0.7 mg/kg doses in a poloxamer gel formulation administered to 4 dogs. Rate of absorption was calculated by Wagner’s modification of the Loo-Riegelman equation (2). The multiplication of rate of absorption by a factor of 5 was selected to deliberately position the rate of absorption profile close the plasma concentration-time profile, thus facilitating comparison of the two functions. Figure 1 illustrates a "flip-flop" pharmacokinetic system. Note the rapidity of intravenous growth hormone (GH) disposition compared to the profile following subcutaneous dosing of the gel formulation. GH intravenous disposition is biexponential, with disposition half-lives of 0.0687 and 0.574 hours. The more rapid exponential term virtually completely disappears after about ten half-lives (0.687 hours), after which intravenous disposition becomes monoexponential. Additionally and more importantly, Equation 1 is applicable to extravascular plasma concentration-time profiles after 0.687 hours, since the only significant influences impacting the GH plasma concentration-time profile derive from absorption and terminal exponential disposition processes. Applying Equation 1 to plasma concentration-time data for the subcutaneous formulation at 48 and 72 hours, DC/Dt = 0.0375 ng/mL/hour. At the midpoint of this time period (60 hours), (K)(C) = 4.55 ng/mL/hr. Since KC >> DC/Dt, rate of absorption » rate of elimination, and a "flip-flop" condition exits. Even though this was established using absorption phase, terminal exponential data, the "flip-flop" condition exists throughout most of the profile, since the downward slope of the profile from the gel formulation never approaches the steepness of the plasma concentration-time function following IV doses. As noted above ("trick"), the plasma concentration-time profile from the gel formulation closely mirrors the rate of absorption profile. This provides an easy way to access the shape of an absorption rate profile in a "flip-flop" model. ReferencesCorresponding author: Harold Boxenbaum, Arishel Inc., 14621 Settlers Landing Way, North Potomac, Maryland, 20878-4305, USA, email:shelbyb@ix.netcom.com Keywords: Pharmacokinetic, Flip-Flop, Growth Hormone
Published by the Canadian Society for Pharmaceutical Sciences. Copyright © 1998 by the Canadian Society for Pharmaceutical Sciences. |