Laboratory Generation of Internal Waves from Topography

Experiments/Research performed by Dawn Aguilar,
May 2004 - August 2005,
Department of Mathematical and Statistical Sciences, University of Alberta

Background

It is well known that internal waves are generated when stratified fluid flows over topography. Examples of environmental stratified flows over topography include the flow of air over mountain ranges and tides over the rough terrain of the ocean floor. In the atmosphere, internal waves launched by air flow over mountains can greatly affect the mean winds and thus, the general circulation of the atmosphere. Similarly, internal waves launched in the ocean are a significant source of mixing and so may influence the Earth's climate.

Despite their importance, the mechanisms by which internal waves are generated from topography are poorly understood beyond the suppositions of linear and inviscid theories. The main limitation of these theories is that they neglect the processes of boundary layer separation and turbulence, both of which are important in the ocean and atmosphere. In these experiments, we explore the effects of boundary layer separation and turbulence on wave generation and compare our results with linear theory predictions.

Experimental Set-up

Experiments were performed in a 2-meter long glass tank filled with uniformly salt-stratified fluid. Model topographies of different shapes (sinusoidal, triangular and rectangular) were towed along the surface at varying speeds, exciting internal waves at frequencies both above and below the buoyancy frequency, N. We define the horizontal Froude number as the excitation frequency normalized by the buoyancy frequency, that is Frh=Uk/N, where U is the towing speed and 1/k is the horizontal length scale of the topography. According to linear theory, propagating internal waves should be generated when Frh<1 and the waves should be evanescent (that is, exponentially decaying) otherwise.

Front view of tank and towing apparatus

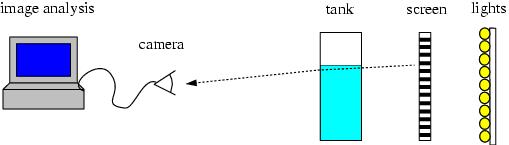
Experiments were recorded using a digital camera situated approximately 340 cm in front of the tank. Two sample recordings of experiments using large sinusoidal hills are provided below. Notice the screen of horizontal black and white lines, which is situated behind the tank and illuminated by fluorescent lighting.

Sample recordings of experiments using large sinusoidal hills

Slow towing speed, Frh=0.61 (43.3MB)

Fast towing speed, Frh=1.29 (30.0MB)

Side view of experimental apparatus, illustrating synthetic schlieren

The waves themselves were visualized and their characteristics measured using the non-obtrusive optical technique, ''synthetic schlieren''. The technique records the distortion of the image of horizontal lines due to the bending of light through different density gradients. An example is provided below, which shows snapshots of an experiment taken (a) at the start of the experiment and (b) during the experiment. The qualitative schlieren image in (c), obtained by taking the difference between the images in (a) and (b), clearly reveals the regions of greatest distortion, namely the wave crests and troughs.

Example illustrating synthetic schlieren technique

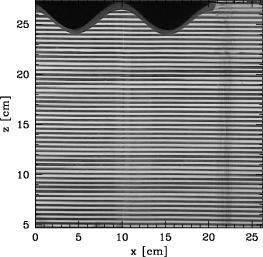
(a) Initial image

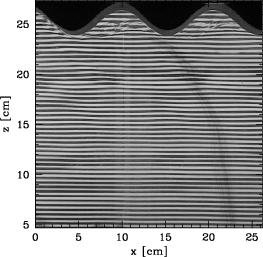
(b) Image during experiment

Qualitative Results

Here we present movies illustrating the development of the internal wave field for different model hills and towing speeds. The images have been flipped vertically for convenience in imagining flow over bottom topography. The raw image of the near-hill region is placed at the bottom of the frame, above which is the internal wave field. Wave crests and troughs are visualized by bands of red and blue respectively.

As you view these movies, pay attention to the different types of waves that emerge. For Frh<1, we observe a uniform wave field directly over the hills. The wave beams extend upwards and to the right as time evolves. For Frh>1, the waves generated directly above the hills do not propagate, consistent with the linear theory prediction that these waves should be evanescent. However, propagating waves are observed in the lee of the last hill, generated in part by flow over the trailing slope. For the steep triangular and rectangular hills, a third set of waves is observed further in the lee. These smaller-scale waves radiate away from a turbulent mixed region.

Smooth Sinusoidal Hills

Slow towing speed, Frh=0.57 (10.1MB)	Fast towing speed, Frh=1.38 (6.1MB)

Slow towing speed, Frh=0.61 (11.1MB)	Fast towing speed, Frh=1.29 (6.5MB)

Rough Triangular and Rectangular Hills

Slow towing speed, Frh=0.45 (11.2MB)	Fast towing speed, Frh=2.13 (9.4MB)

Slow towing speed, Frh=0.35 (10.8MB)	Fast towing speed, Frh=1.74 (9.4MB)

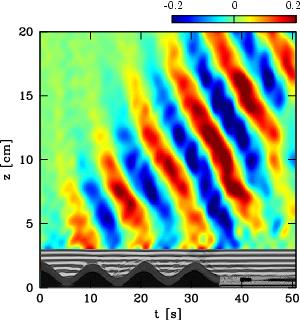
We use vertical time series images to identify the mechanisms of wave generation. Here we present three experiments that are representative of the different ways in which internal waves may be generated from topography. The three mechanisms are summarized below: (1) Topographic forcing refers to the flow of fluid into and out of the valleys and results in a regular wave field. By comparing the distance between successive crests or troughs and that between successive hilltops, we notice that they are approximately the same. This is consistent with the linear theory prediction that the wave frequency should match the excitation frequency. (2) The term "boundary-trapped lee wave" refers to the undular shear layer trailing the last hill, which is identified by the distortion of the image of black and white lines (T=14-21s). Vertically-propagating internal waves are generated directly in the lee of the last hill in part by fluid flowing over boundary-trapped lee waves. (3) Turbulence is created far in the lee of topography, provided the towing speed is sufficiently fast and the topography sufficiently steep, and results in the generation of small-scale internal waves (T=28-48s).

(1) Topographic forcing	(2) Boundary-trapped lee waves	(3) Turbulence
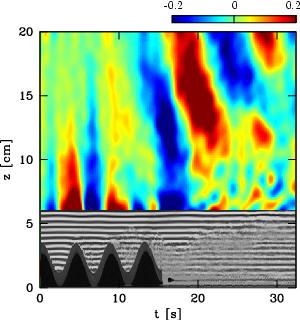
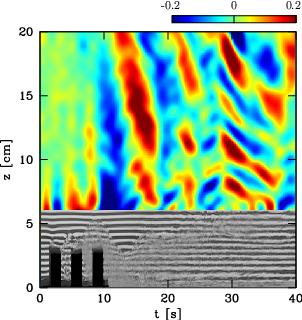
Small sinusoidal hills, Frh=0.57	Large sinusoidal hills, Frh=1.29	Rectangular hills, Frh=1.74

Quantitative Results

Here, we present plots of internal wave frequency and amplitude for the different types of waves generated in the experiments. For all plots, the horizontal axis is the horizontal Froude number (that is, the normalized excitation frequency), a vertical line at Frh=1 divides the plot into two regimes, and the linear theory prediction is given by a thick solid line. We begin with the results of the small and large sinusoidal hill experiments.

Sinusoidal Hills

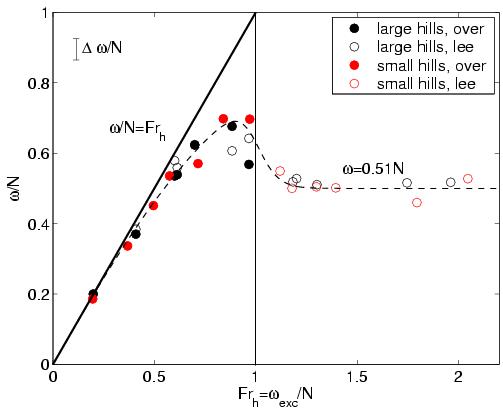
Internal wave frequency	Internal wave amplitude

In terms of wave frequency, experimental measurements agree well with linear theory predictions for Frh<0.7, above which occur significant departures. When Frh>1, waves are still generated in the lee and have frequencies an approximately constant fraction of N, despite the different hill heights and amounts of turbulence generated. In terms of wave amplitude, linear theory overestimates the amplitude in all cases. The reason for the reduced wave amplitudes observed in our experiments is because the fluid does not feel the full height of the hill. Rather, the fluid separates from the lee-side slopes of the hills and forms patches of stagnant fluid in the valleys. This reduces the effective hill height for wave generation. Two images illustrating flow separation and the formation of stagnant fluid are provided below. The depth of the stagnant region increases with increasing H and decreasing Frh.

H=1.3cm, Frh=0.19

H=2.6cm, Frh=0.20

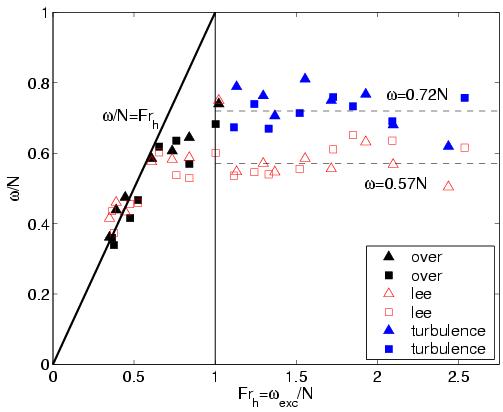
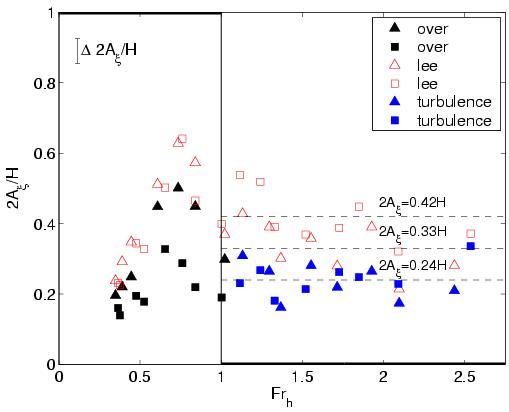
Next, we present the wave frequency and amplitude plots for the steeper triangular and rectangular hills. The characteristics of the waves generated directly over the hills and in the lee of the last hill are similar. Notice the addition of the blue markers, which correspond to the waves generated by the turbulent mixed region. Remarkably, these waves are generated within a narrow range of frequencies, despite the many scales associated with turbulence. This result is consistent with that of other studies involving the generation of waves from turbulence (see for example, Dohan and Sutherland, 2005 ).

Triangular and Rectangular Hills

Internal wave frequency	Internal wave amplitude

Links to related research

Generation of Internal Waves over Sinusoidal Topography,
D. A. Aguilar, B. R. Sutherland and D. J. Muraki, Deep-Sea Research II

Laboratory Generation of Internal Waves from Rough Topography,
D. A. Aguilar and B. R. Sutherland, 15th Conference on Atmospheric and Oceanic Fluid Dynamics

Acknowledgements

This research was financially supported by grants from:

Return to Research Interests page

Bruce's home page

Department of Physics

Department of Earth and Atmospheric Sciences