Hyperbolic lattices are synthetic metamaterials which emulate two-dimensional negatively curved space.
We are curious to know whether they exhibit any topologically nontrivial phases.
In this work, we study the celebrated Haldane model on finite-sized hyperbolic lattices and observe
insulating phases with nontrivial Chern numbers. The image above demonstrates the chiral edge mode
arising from the nontrivial Chern number of the Haldane model on the {5,4} hyperbolic lattice.
Most existing experimental realizations of hyperbolic lattices exhibit a significant boundary-to-bulk ratio.
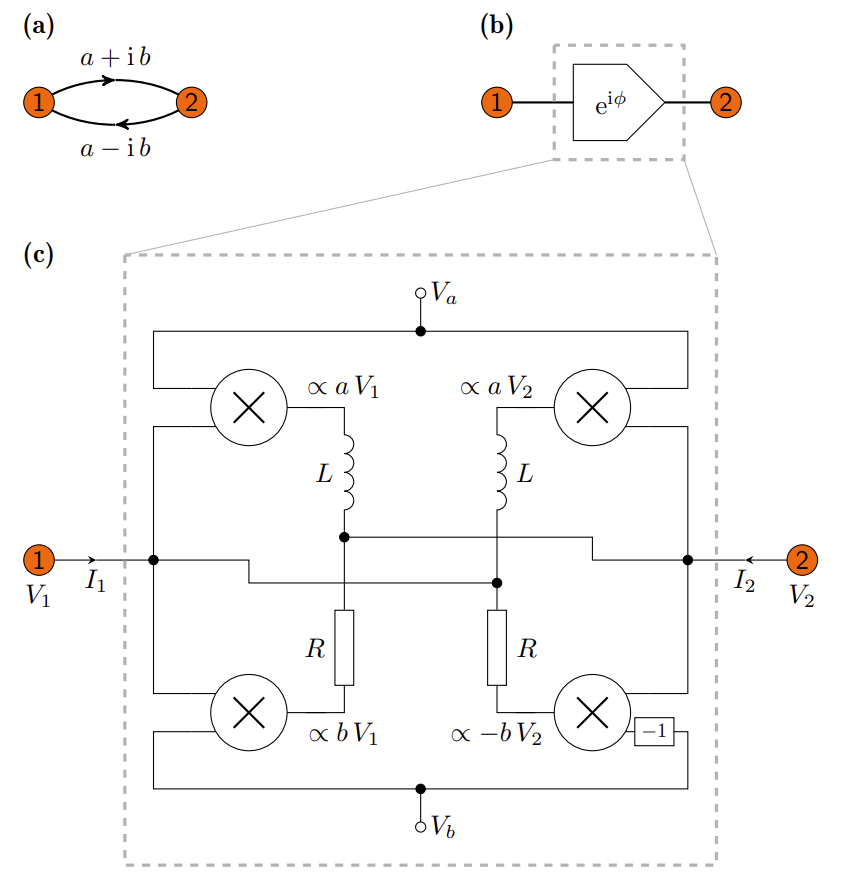
In this work, we design and build an electrical circuit (with a novel
complex-phase element) based on
hyperbolic band theory to simulate the bulk physics of finite-sized
hyperbolic lattices, thereby completely eliminating the boundary effect