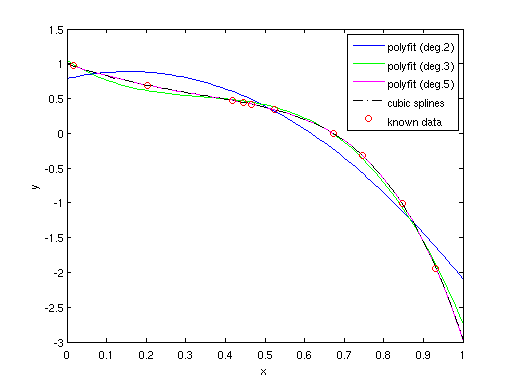
% ________________________________________________________ % File : fitPoly.m % Purpose : fit data in polynomials and show MATLAB % built-in functions about polynomials % Usage : fitPoly % Input : - % Output : - % Last Modified : August 25, 2006 % ________________________________________________________ % original polynomial % y = 1 - 2*x + 3*x.^2 - 4*x.^3 + 5*x.^4 - 6*x.^5 % load data load fitPoly_data.mat % ================= % using polyfit % ================= % ----------------- % in quadratic polynomial p1 = polyfit(x, y, 2) % ----------------- % in cubic polynomial p2 = polyfit(x, y, 3) % ----------------- % in polynomial of degree 5 p3 = polyfit(x, y, 5) % ================= % using spline % ================= splineInfo = spline(x,y) splineInfo.coefs % ----------------- % predict y with specific x y_x = ppval( splineInfo, [0.2]) % display results X = 0:0.01:1; plot(X, polyval( p1, X), '-b',... X, polyval( p2, X), '-g',... X, polyval( p3, X), '-m',... X, ppval( splineInfo, X), '-.k',... x, y, 'or') legend('polyfit (deg.2)',... 'polyfit (deg.3)',... 'polyfit (deg.5)',... 'cubic splines',... 'known data') xlabel('x') ylabel('y') % ================= % other MATLAB built-in functions dealing with polynomials % ================= % ----------------- % Polynomial derivative (polyder) der = polyder( p3) % ----------------- % Integrate polynomial analytically (polyint) % - - - - - - - - - % assume a constant of integration k=0 int0 = polyint( der) % - - - - - - - - - % use a scalar constant of integration k=1 int = polyint( der, 1) % ----------------- % Convolution and polynomial multiplication (conv) v = [1 5 10]; w = conv( p3, v) % ----------------- % Deconvolution and polynomial division (deconv) [q,r] = deconv( w, v) % q = quotient; r = remainder
OUTPUT:
p1 =
-4.1996 1.3125 0.7841
p2 =
-10.0806 10.0958 -3.8185 1.0542
p3 =
-6.0000 5.0000 -4.0000 3.0000 -2.0000 1.0000
splineInfo =
form: 'pp'
breaks: [1x10 double]
coefs: [9x4 double]
pieces: 9
order: 4
dim: 1
ans =
-3.2925 3.1183 -1.9584 0.9701
-3.2925 1.2675 -1.1367 0.6910
-11.2272 -0.8660 -1.0499 0.4714
-6.9042 -1.7568 -1.1193 0.4429
-7.2514 -2.1896 -1.2018 0.4186
-13.7055 -3.4766 -1.5370 0.3384
-20.0358 -9.5201 -3.4473 -0.0062
-27.3613 -14.0070 -5.2036 -0.3249
-27.3613 -22.1691 -8.8008 -1.0077
y_x =
0.6940
der =
-30.0000 20.0000 -12.0000 6.0000 -2.0000
int0 =
-6.0000 5.0000 -4.0000 3.0000 -2.0000 0
int =
-6.0000 5.0000 -4.0000 3.0000 -2.0000 1.0000
w =
Columns 1 through 7
-6.0000 -25.0000 -39.0000 33.0000 -27.0000 21.0000 -15.0000
Column 8
10.0000
q =
-6.0000 5.0000 -4.0000 3.0000 -2.0000 1.0000
r =
1.0e-12 *
Columns 1 through 7
0 0 0 0 0 0 0.5720
Column 8
-0.0071