Ch E 416 - Assignment 1 Solutions

Question 1

(a) Using the MATLAB code and thermophysical properties given with the assignment, fugacity data was obtained and plotted for propane. Liquid and vapor fugacities are equal at the saturation point.

(b) By inspection of the plot, the saturation temperature appears to be approximately 287.0 K (= 13.85 ⁰C). This agrees quite well with the literature value of T_sat = 286.53 K from NIST database.

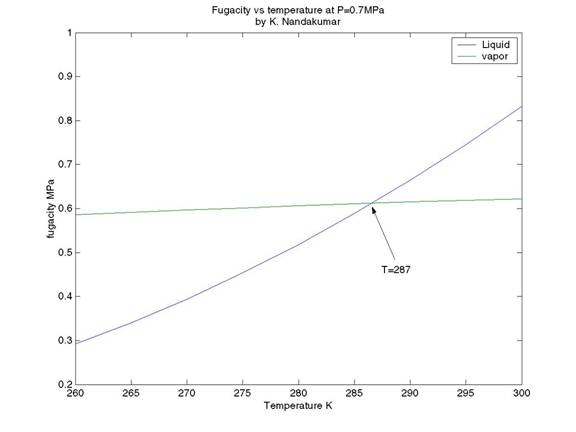
One can also solve precisely for the saturation temperature by making the fugacities equal in both the phases. The following function can be used with “fsolve” in MATLAB to solve the problem.

function f=A1_Tb(T,P,Tc,Pc,w)

%to find the value of T that makes the difference between fg and fl zero

%use MATLAB function fsolve.

%options=optimset('Display','Iter');

%fsolve('A1_Tb',230,options,0.7,369.83,4.245517,0.152291)

[fl,fg]=A1_fugT(T,P,Tc,Pc,w);

f=fl-fg;

end

Here are the results.

options=optimset('Display','Iter');
fsolve('A1_Tb',230,options,0.7,369.83,4.245517,0.152291)

Norm of First-order

Iteration Func-count f(x) step optimality CG-iterations

1 3 0.197851 1 0.000999 0

2 5 0.171089 10 0.00166 1

3 7 0.0864436 20 0.00237 1

4 9 0.0228214 36.4924 0.00247 1

5 11 9.09319e-005 9.23661 0.000136 1

6 13 2.62979e-009 0.668027 7.24e-007 1

Optimization terminated successfully:

First-order optimality less than OPTIONS.TolFun, and no negative/zero curvature detected

ans =

286.5878

[fl,fg,zL,zG]=A1_fugT(286.5878,0.7,369.83,4.245517,0.152291)

fl =

0.6120

fg =

0.6120

zL =

0.0242

zG =

0.8576

> rhoL=0.7/8.314472E-3/zL/286.5878

rhoL =

12.1339 %mol/l

>> rhoG=0.7/8.314472E-3/zG/286.5878

rhoG =

0.3426 %mol/l

%Note from NIST data base, the values are: (11.558,0.34412) mol/l

(d) Using the ASPEN simulator with the RK-ASPEN EOS to calculate pure component properties, the following graph was generated for the fugacity coefficient PHI. The saturation temperature appears to be T = 286.5 K.

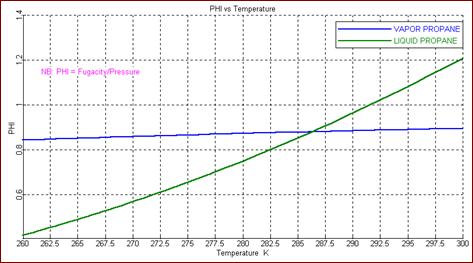
(e) From the two plots at T = 280 K, the PR-EOS gives f^L= 5.12 bar and f^V = 6.05 bar, for the liquid and vapor phase fugacities, respectively. The RK-ASPEN EOS gives approximately f^L= 5.25 bar and f^V = 6.16 bar.

Question 2

(a) The previous MATLAB code was modified to determine fugacities over a range of pressures. Again, the thermophysical properties given at the end of the assignment were used. Once fugacity data was generated, it was plotted.

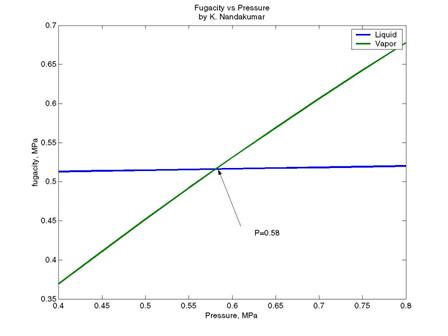
(b) At a given temperature (T=280 K), liquid and vapour fugacities are equal at the saturation pressure. By inspection of the plot, the saturation pressure at 280 K appears to be approximately 0.58 MPa. It can also be computed more precisely using “fsolve” that makes the fugacities equal by varying the Pressure. Here is how it works:

function f=A1_Pv(P,T,Tc,Pc,w)

%to find the value of P that makes the difference between fg and fl zero

%use MATLAB function fsolve.

%options=optimset('Display','Iter');

%fsolve('A1_Pv',0.5,options,280,369.83,4.245517,0.152291)

[fl,fg]=A1_fugT(T,P,Tc,Pc,w);

f=fl-fg;

end

Here are the results.

>> fsolve(‘A1_Pv’,0.5,options,280,369.83,4.245517,0.152291)

Norm of First-order

Iteration Func-count f(x) step optimality CG-iterations

1 3 0.00393073 1 0.0496 0

2 5 1.41227e-006 0.0792466 0.000905 1

3 7 2.12884e-013 0.0015613 3.51e-007 1

Optimization terminated successfully:

First-order optimality less than OPTIONS.TolFun, and no negative/zero curvature detected

ans =

0.5808 %Sat Press in MPa

From NIST database, the saturation pressure at T=280 K is P=0.58189 Mpa
very close! Look at the power of equations of state!

Question 3

The binary interaction parameters (k_ij's) from HYSYS are (with methane=1,ethane=2, n-propane=3):
k₁₁ = k₂₂ = k₃₃ = 0
k₁₂ = k₂₁ = 0.00224
k₁₃ = k₃₁ = 0.00683
k₃₂ = k₂₃ = 0.00126
Now, writing the necessary equations as MATLAB code and using the thermophysical properties given in the table at the end of the assignment, we find:

T = 224.8168; % K

P = 13.7895; % bar

y = [0.4 0.4 0.2];

Tc = [190.6 305.4 369.8]; % K

Pc = [45.4 48.2 41.9]*1.01325; % bar

w = [0.008 0.099493 0.152291];

k(3,3)=0; % interaction of species with itself

k(1,2)=2.24e-003;

k(2,1)=k(1,2);

k(2,3)=1.26e-003;

k(3,2)=k(2,3);

k(1,3)=6.83e-003;

k(3,1)=k(1,3);

fugV = A1_fug_mix(T,P,y,Tc,Pc,w,k)

fugV =

5.3957 4.2073 1.7033

===============NOTE=================

*** These values are expressed in bar ***

Question 4

The binary interaction parameter is obtained from HYSYS. k_1,2=0.00258

Experimental values of equilibrium ratios:
K₁=y₁/x₁=0.6650/0.2900=2.293
K₂=y₂/x₂=(1-0.6650)/(1-0.2900)=0.3350/0.7100=0.472
a₁₂=K₁/K₂=2.293/0.472=4.86

From Raoult’s law:
K₁=P₁^s/P=409.6/147=2.786
K₂=P₂^s/P=58.6/147=0.399
a₁₂=K₁/K₂=2.786/0.399=6.98

K-values from an EOS:

F_L,1(T,P,x₁,x₂)= F_V,1(T,P,y₁,y₂)
F_L,2(T,P,x₁,x₂)= F_V,2(T,P,y₁,y₂)
x₁+x₂=1
y₁+y₂=1

Given (T=167 ^oF, P=147 psia), solve the above four equations given in the function A1_Kval_PR for the unknowns using fsolve. The script file used is A1_P4.m. The results are given below:

options=optimset('TolFun',1e-6,'Display','Final');

xx=fsolve('A1_Kval_PR',[.29 .71 0.665 0.335],options);

x = xx(1:2)

y = xx(3:4)

K = y./x

alpha_12 = K(1)/K(2)

Optimization terminated: first-order optimality is less than options.TolFun.

x =

0.29066 0.70934

y =

0.66025 0.33975

K =

2.2715 0.47897

alpha_12 =

4.7425

a₁₂=K₁/K₂= 4.7425 (Compares well with the experimental value of 4.86)

Notes:

(1) The code given is based on temperatures in K and pressures in bar (not atm). To use this code you needed to enter all thermophysical property data in the correct units.
(2)Fugacity has the same units as pressure!

Posted Sept 22, 2006

Return to Assignments Page